Come eseguire un test post hoc di tukey-kramer in excel

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Le ipotesi utilizzate in un’ANOVA sono le seguenti:

Ipotesi nulla (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (le medie sono uguali per ciascun gruppo)

Ipotesi alternativa: (Ha): almeno una delle medie è diversa dalle altre

Se il valore p dell’ANOVA è inferiore al livello di significatività, possiamo rifiutare l’ipotesi nulla e concludere che abbiamo prove sufficienti per affermare che almeno una delle medie del gruppo è diversa dalle altre.

Tuttavia, questo non ci dice quali gruppi siano diversi gli uni dagli altri. Questo ci dice semplicemente che non tutte le medie dei gruppi sono uguali. Per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo eseguire un test post hoc.

Il test post hoc più comunemente utilizzato è il test di Tukey-Kramer , che confronta la media tra ciascuna combinazione di gruppi a coppie.

L’esempio seguente mostra come eseguire il test di Tukey-Kramer in Excel.

Esempio: test di Tukey-Kramer in Excel

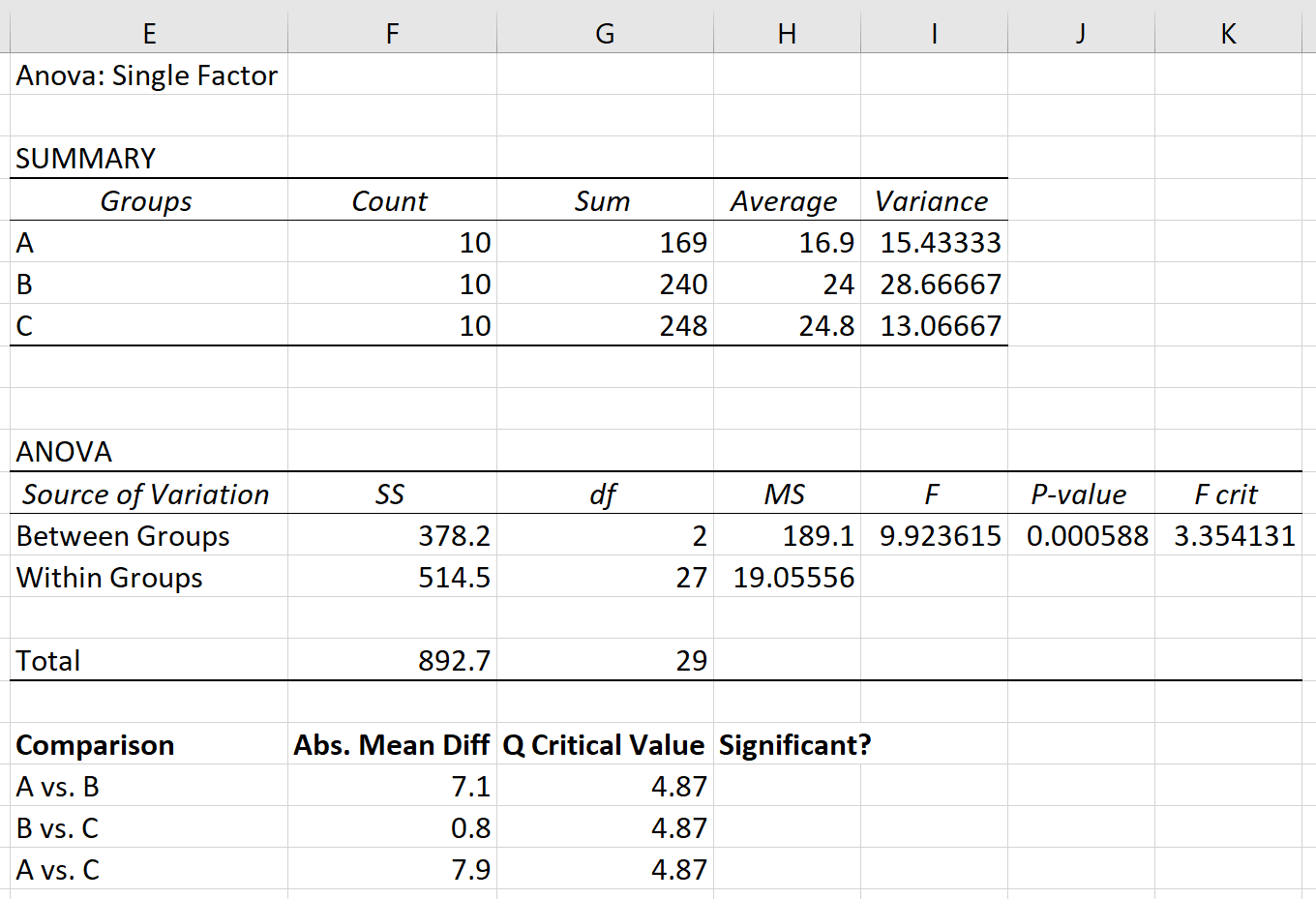
Supponiamo di eseguire un’ANOVA unidirezionale su tre gruppi: A, B e C. I risultati dell’ANOVA unidirezionale sono mostrati di seguito:

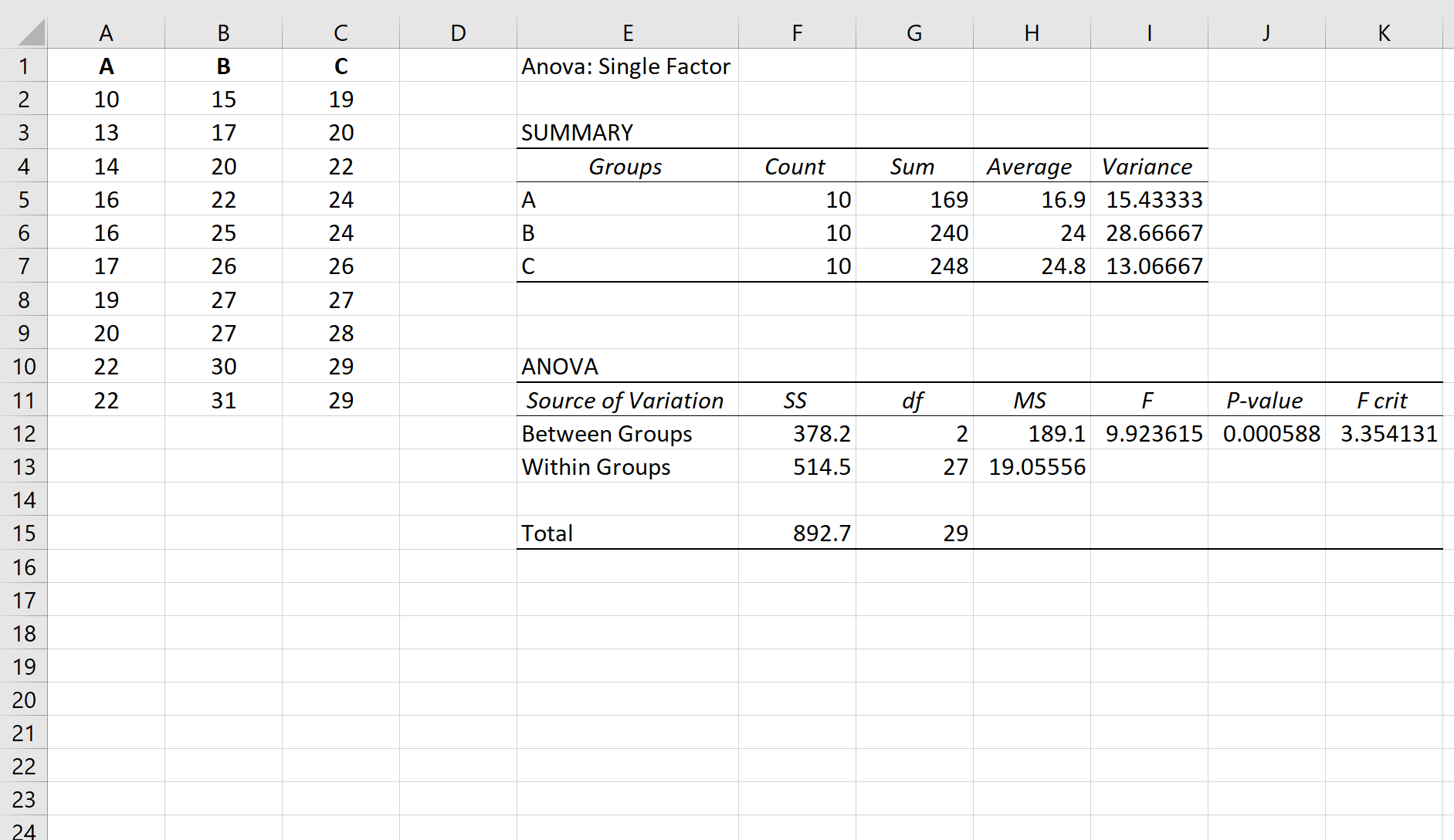
Correlati: Come eseguire ANOVA unidirezionale in Excel

Il valore p della tabella ANOVA è 0.000588 . Poiché questo valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla e concludere che le medie tra i tre gruppi non sono uguali.

Per determinare esattamente quali medie di gruppo sono diverse, possiamo eseguire un test post hoc di Tukey-Kramer utilizzando i seguenti passaggi:

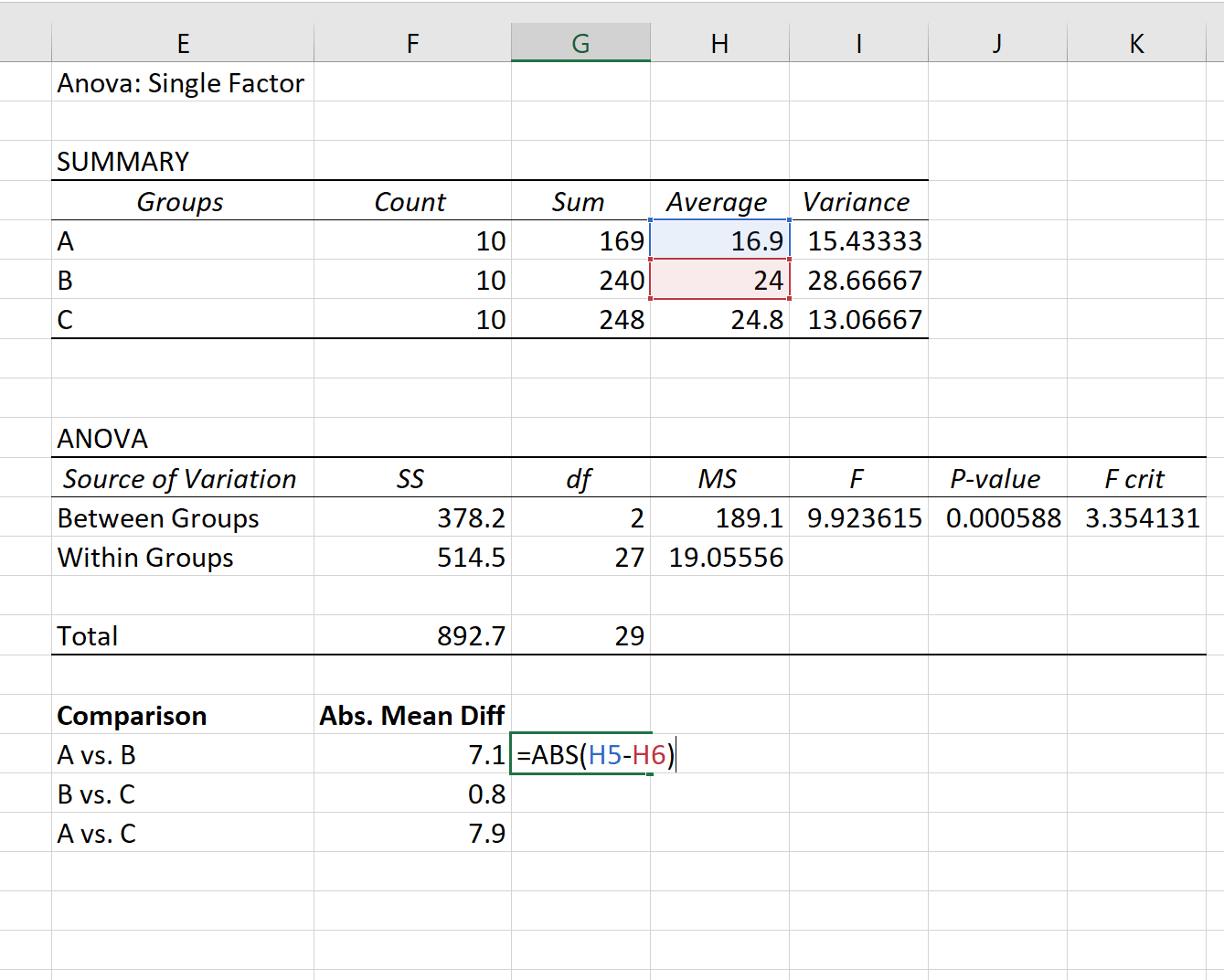
Passaggio 1: trovare la differenza media assoluta tra ciascun gruppo.

Innanzitutto, troveremo la differenza media assoluta tra ciascun gruppo utilizzando le medie elencate nella prima tabella del risultato ANOVA:

Passaggio 2: Trova il valore critico di Q.

Successivamente, dobbiamo trovare il valore critico di Q utilizzando la seguente formula:

Valore critico Q = Q*√(s ² _raggruppati / n.)

Oro:

• Q = Valore dell’intervallo della Tabella Studenti Q
• s ² _aggregato = varianza aggregata tra tutti i gruppi
• non. = Dimensione del campione per un dato gruppo

Per trovare il valore Q, puoi fare riferimento alla tabella Q dell’intervallo studentizzato che assomiglia a questa:

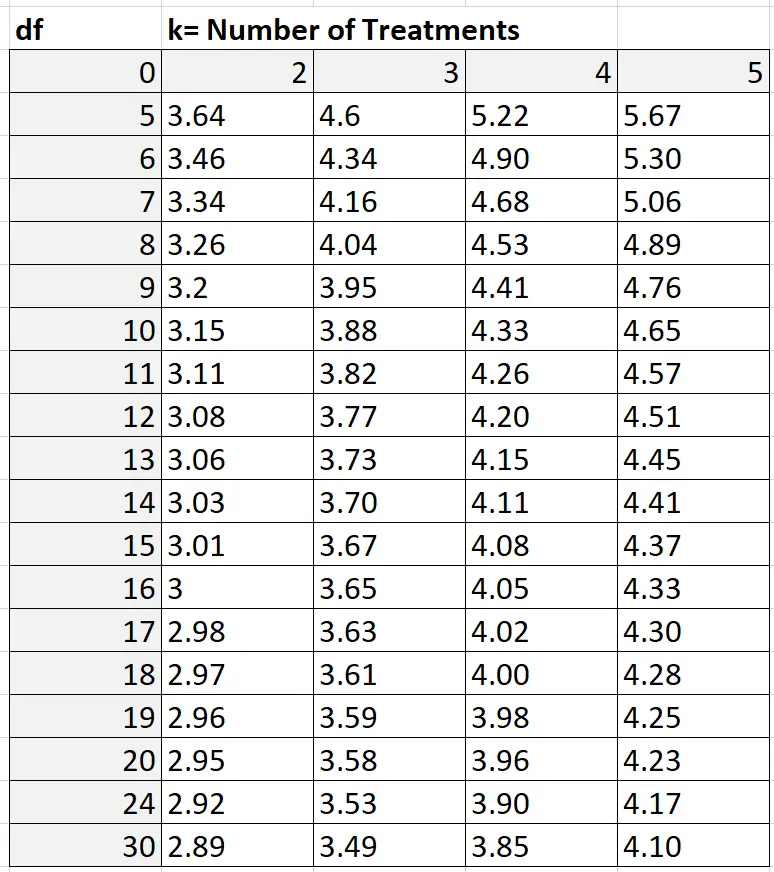
Nel nostro esempio, k = numero di gruppi, ovvero k = 3. I gradi di libertà sono calcolati come: nk = 30 – 3 = 27. Poiché 27 non è mostrato nella tabella sopra, possiamo utilizzare una stima conservativa di 24 Basandosi su k = 3 e df = 24, troviamo che Q = 3,53 .

La varianza aggregata può essere calcolata come la media delle varianze dei gruppi, che risulta essere 19.056 .

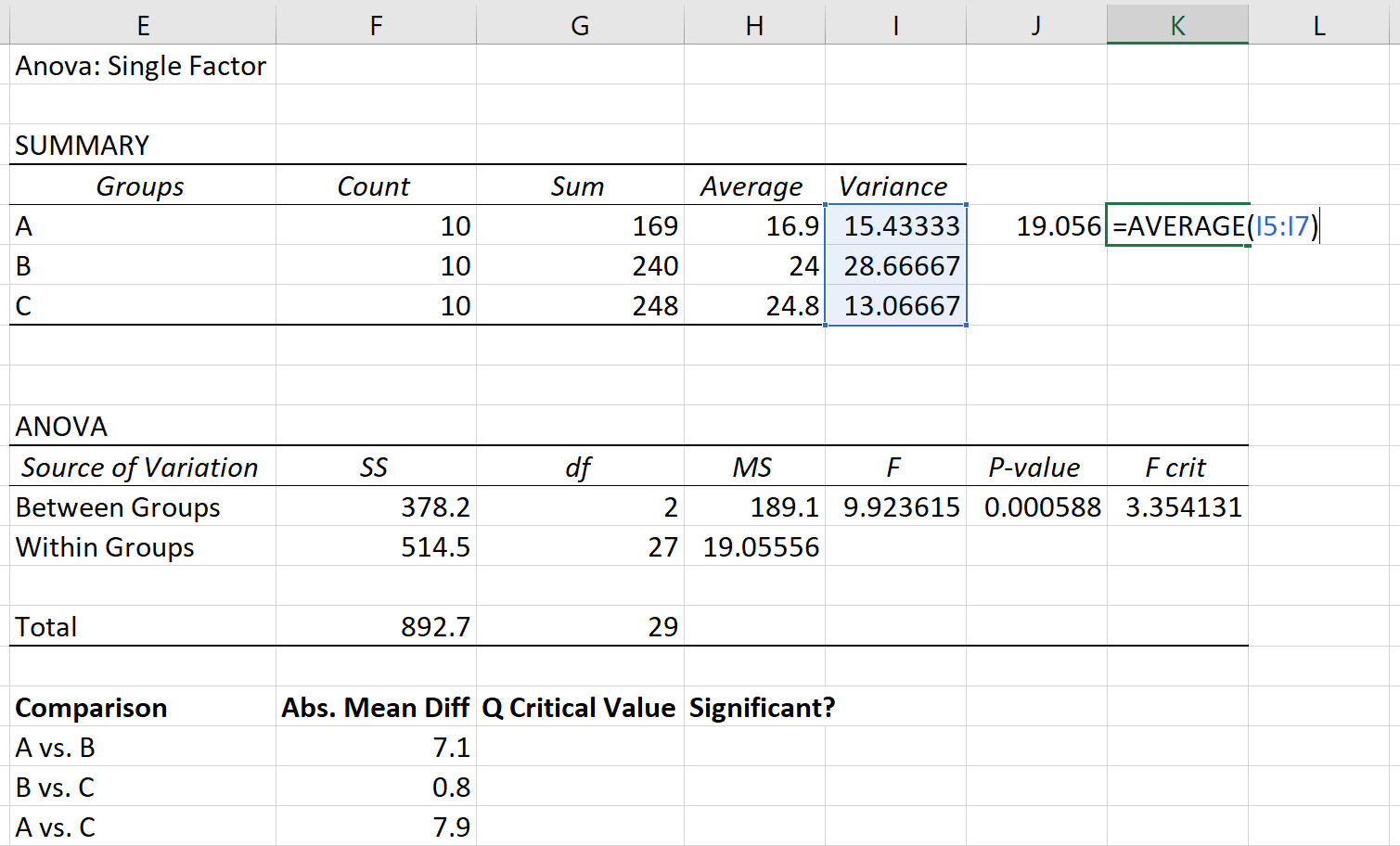
Infine, la dimensione del campione di ciascun gruppo è 10.

Pertanto, il nostro valore critico Q può essere calcolato come segue:

Valore critico Q = Q*√(s ² _raggruppati / n.) = 3,53*√(19,056/10) = 4,87 .

Passaggio 3: determinare quali medie di gruppo sono diverse .

Infine, possiamo confrontare la differenza media assoluta tra ciascun gruppo con il valore critico Q. Se la differenza media assoluta è maggiore del valore critico Q, allora la differenza tra le medie del gruppo è statisticamente significativa:

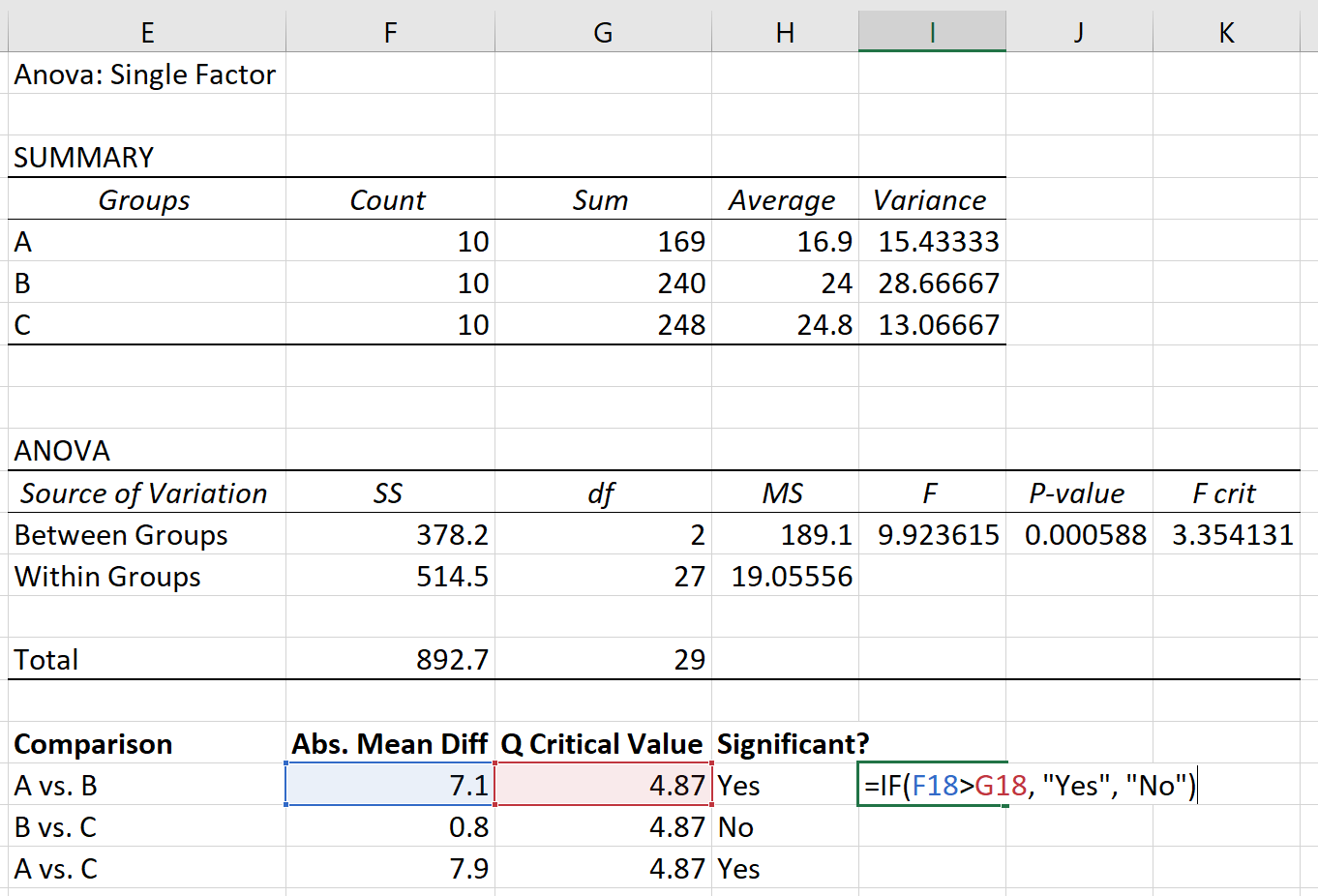
Sulla base del test post hoc di Tukey-Kramer, abbiamo trovato quanto segue:

• La differenza nelle medie tra il gruppo A e il gruppo B è statisticamente significativa.
• La differenza nelle medie tra il gruppo B e il gruppo C non è statisticamente significativa.
• La differenza nelle medie tra il gruppo A e il gruppo C è statisticamente significativa.

Risorse addizionali

Come eseguire ANOVA unidirezionale in Excel
Una guida all’utilizzo dei test post-hoc con ANOVA