Cos'è un test multinomiale? (definizione & #038; esempio)

Un test multinomiale viene utilizzato per determinare se una variabile categoriale segue una distribuzione ipotetica.

Questo test utilizza le seguenti ipotesi nulle e alternative:

H ₀ : Una variabile categoriale segue una distribuzione ipotetica.

H _A : Una variabile categoriale non segue la distribuzione ipotetica.

Se il p-value del test è inferiore ad un certo livello di significatività (es. α = 0,05), allora possiamo rifiutare l’ipotesi nulla e concludere che la variabile non segue la distribuzione ipotizzata.

Questo test viene utilizzato quando una variabile può assumere k risultati diversi. Un classico esempio di test multinomiale è quello in cui vogliamo determinare se alcuni dadi sono equi. Quando lanci un dado, la probabilità che esca su ciascun numero (da 1 a 6) è 1/6.

Per verificare se un dado è giusto, potremmo lanciarlo un certo numero di volte e vedere se il numero di volte in cui esce su numeri diversi è significativamente diverso da quello che ci aspetteremmo.

Gli esempi seguenti mostrano come eseguire un test multinomiale utilizzando il linguaggio di programmazione statistica R.

Esempio 1: Dadi equilibrati

Supponiamo di voler determinare se un dado è giusto. Per testarlo, lo eseguiamo 30 volte e registriamo la frequenza di ciascun risultato. La tabella seguente mostra i risultati:

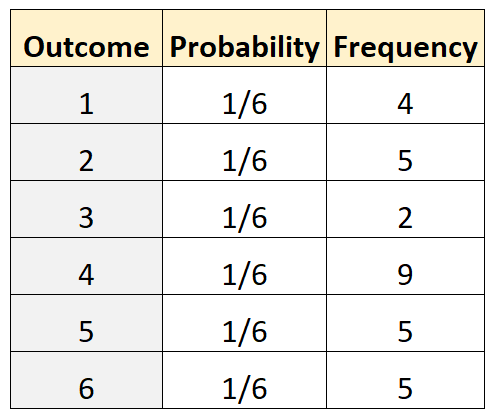
Il seguente codice in R può essere utilizzato per eseguire un test multinomiale:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

Il valore p del test è 0,4306 . Poiché questo valore p non è inferiore a 0,05, non rifiuteremo l’ipotesi nulla. Quindi non abbiamo prove sufficienti per dire che i dadi sono ingiusti.

Esempio 2: vendite di prodotti

Supponiamo che il proprietario di un negozio ipotizzi che un numero uguale di clienti acquisterà ciascuno di quattro prodotti diversi. Per testarlo, registra il numero di clienti che hanno acquistato ciascun prodotto in una determinata settimana. La tabella seguente mostra i risultati:

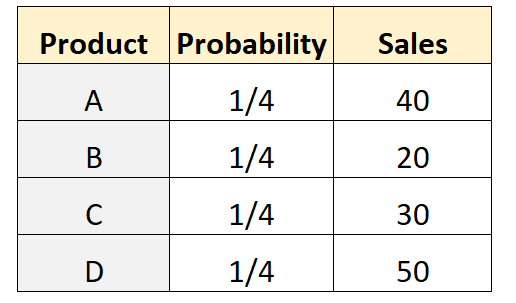
Il seguente codice in R può essere utilizzato per eseguire un test multinomiale su questo set di dati:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

Il valore p del test è 0,00226 . Poiché questo valore p è inferiore a 0,05, rifiuteremo l’ipotesi nulla. Quindi, abbiamo prove sufficienti per affermare che le vendite non sono uguali per ciascun prodotto.

Esempio 3: Biglie in un sacchetto

Tom afferma che la probabilità di scegliere una biglia rossa, verde o viola da un sacchetto è rispettivamente 0,2, 0,5 e 0,3. Per testarlo, il suo amico Mike fruga nella borsa ed estrae una biglia (con le sostituzioni) 100 volte diverse. La tabella seguente mostra i risultati:

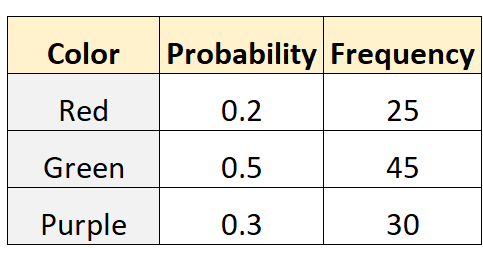
Il seguente codice in R può essere utilizzato per eseguire un test multinomiale su questo set di dati:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

Il valore p del test è 0,3999 . Poiché questo valore p non è inferiore a 0,05, non riusciremo a rifiutare l’ipotesi nulla. Non abbiamo quindi prove sufficienti per affermare che la distribuzione delle biglie nel sacchetto sia diversa da quella specificata da Tom.

Risorse addizionali

Un’introduzione alla distribuzione multinomiale
Calcolatore della distribuzione multinomiale