Come eseguire il test esatto di fisher in spss
Il test esatto di Fisher viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.
Viene generalmente utilizzato come alternativa al test di indipendenza chi quadrato quando uno o più conteggi di celle in una tabella 2 × 2 sono inferiori a 5.
Questo tutorial spiega come eseguire il test esatto di Fisher in SPSS.
Esempio: test esatto di Fisher in SPSS
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico in un particolare college. Per esplorare questo aspetto, abbiamo intervistato in modo casuale 25 studenti del campus. Il numero di studenti democratici o repubblicani, in base al sesso, è mostrato nella tabella seguente:
| Democratico | Repubblicano | |
|---|---|---|
| Femmina | 8 | 4 |
| Maschio | 4 | 9 |
Per determinare se esiste un’associazione statisticamente significativa tra genere e preferenza del partito politico, possiamo utilizzare i seguenti passaggi per eseguire il test esatto di Fisher in SPSS:
Passaggio 1: inserisci i dati.
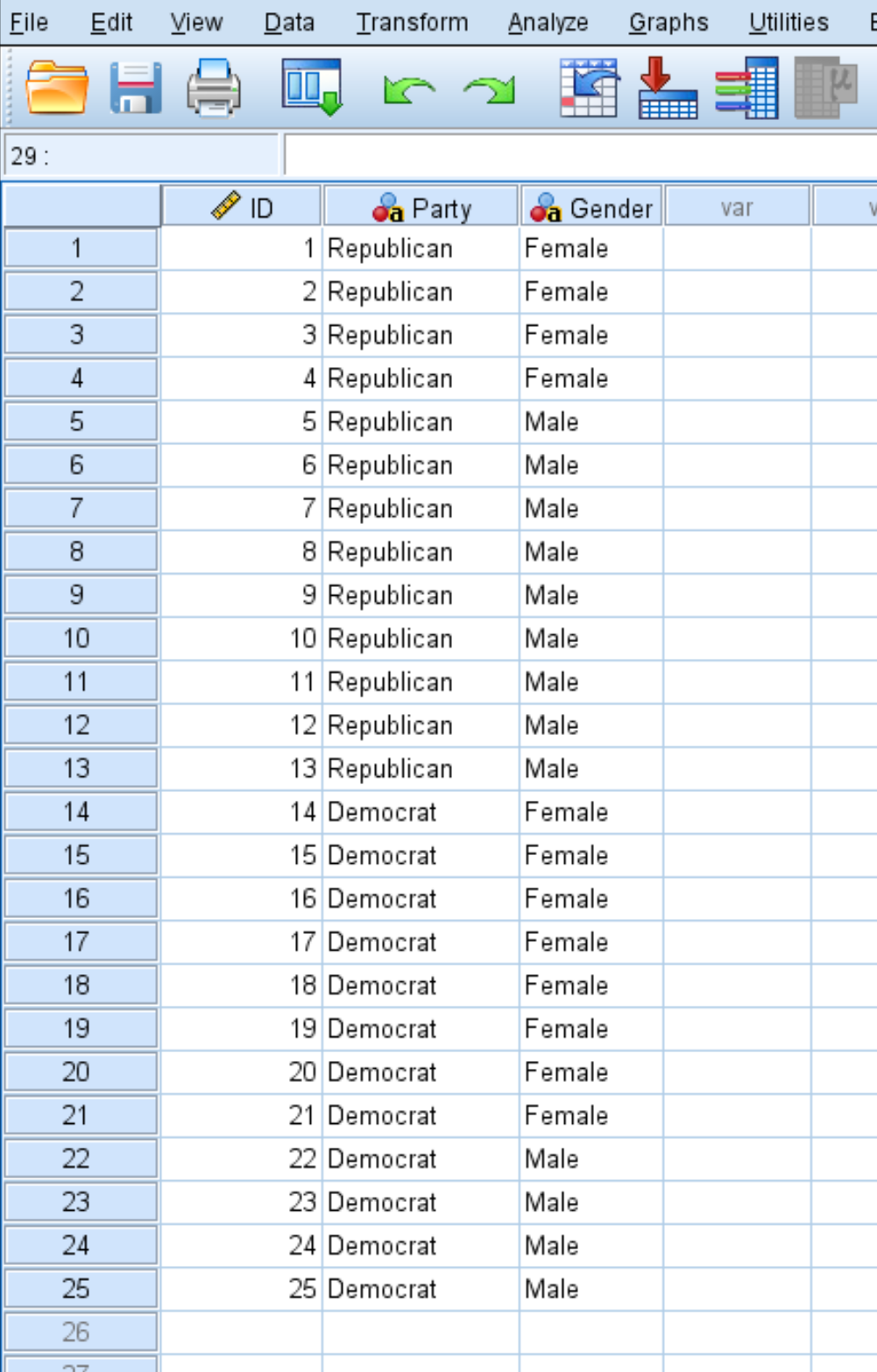
Innanzitutto, inserisci i dati come mostrato di seguito:
Ogni riga mostra l’ID di un individuo, la preferenza del partito politico e il sesso.
Passaggio 2: eseguire il test esatto di Fisher.
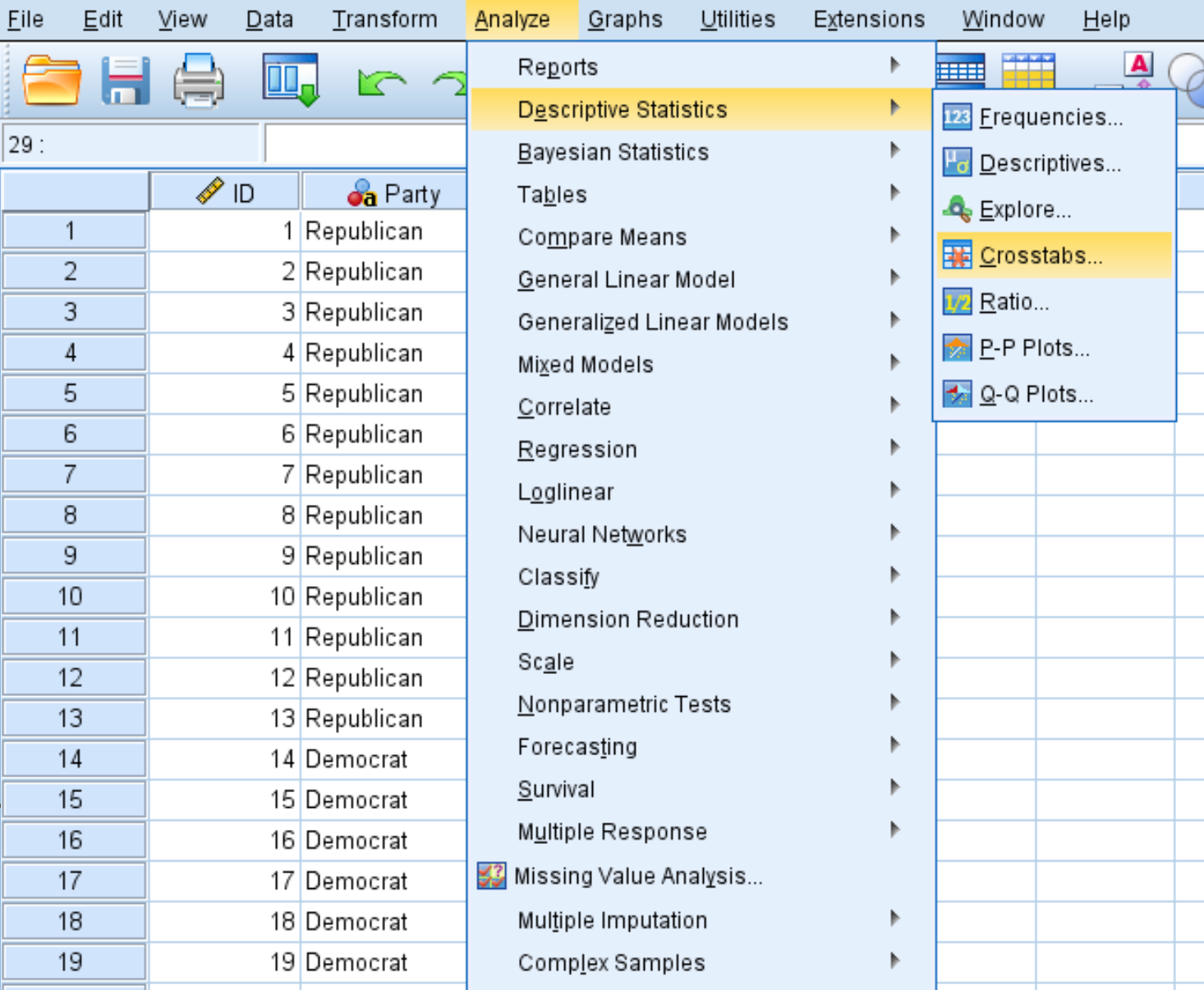
Fare clic sulla scheda Analizza , quindi su Statistiche descrittive e quindi su Tabelle incrociate :
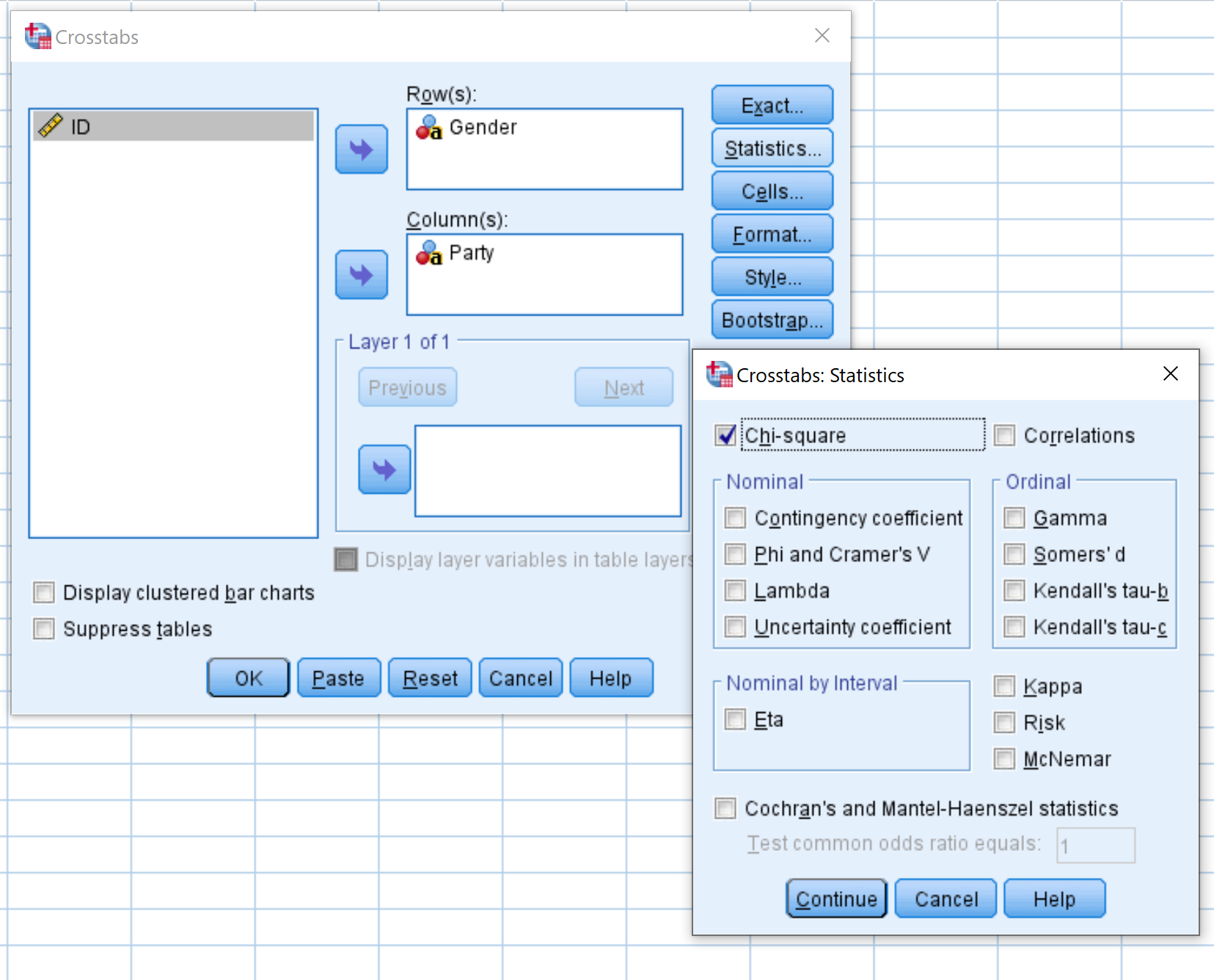
Trascina la variabile Sesso nell’area denominata Righe e la variabile Parte nell’area denominata Colonne. Quindi fai clic sul pulsante denominato Statistiche e assicurati che la casella accanto a Chi quadrato sia selezionata. Quindi fare clic su Continua .
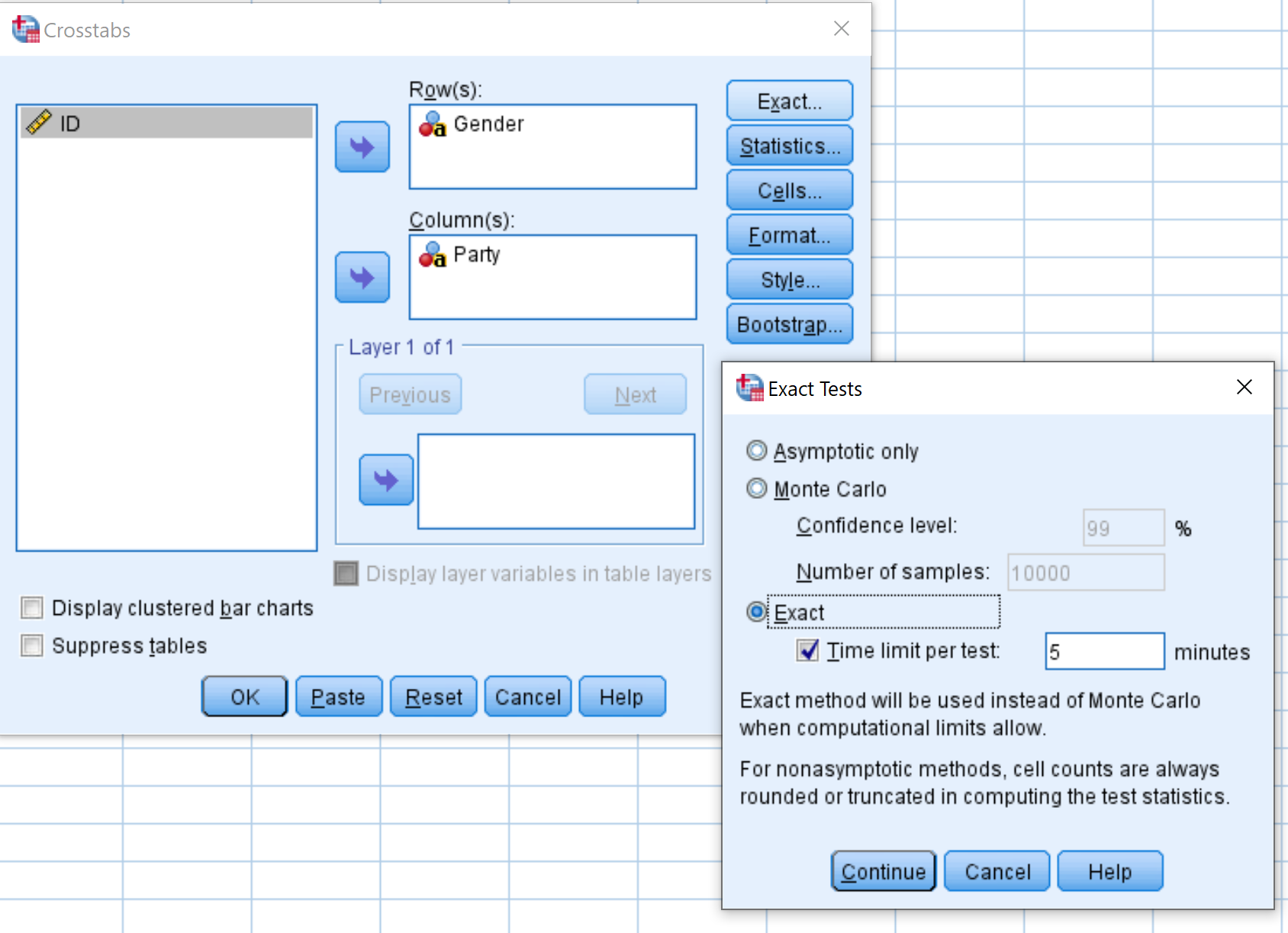
Successivamente, fai clic sul pulsante etichettato Esatto e assicurati che la casella accanto a Esatto sia selezionata. Quindi fare clic su Continua .
Infine, fare clic su OK per eseguire il test esatto di Fisher.
Passaggio 3: interpretare i risultati.
Dopo aver fatto clic su OK , verranno visualizzati i risultati esatti del test di Fisher:
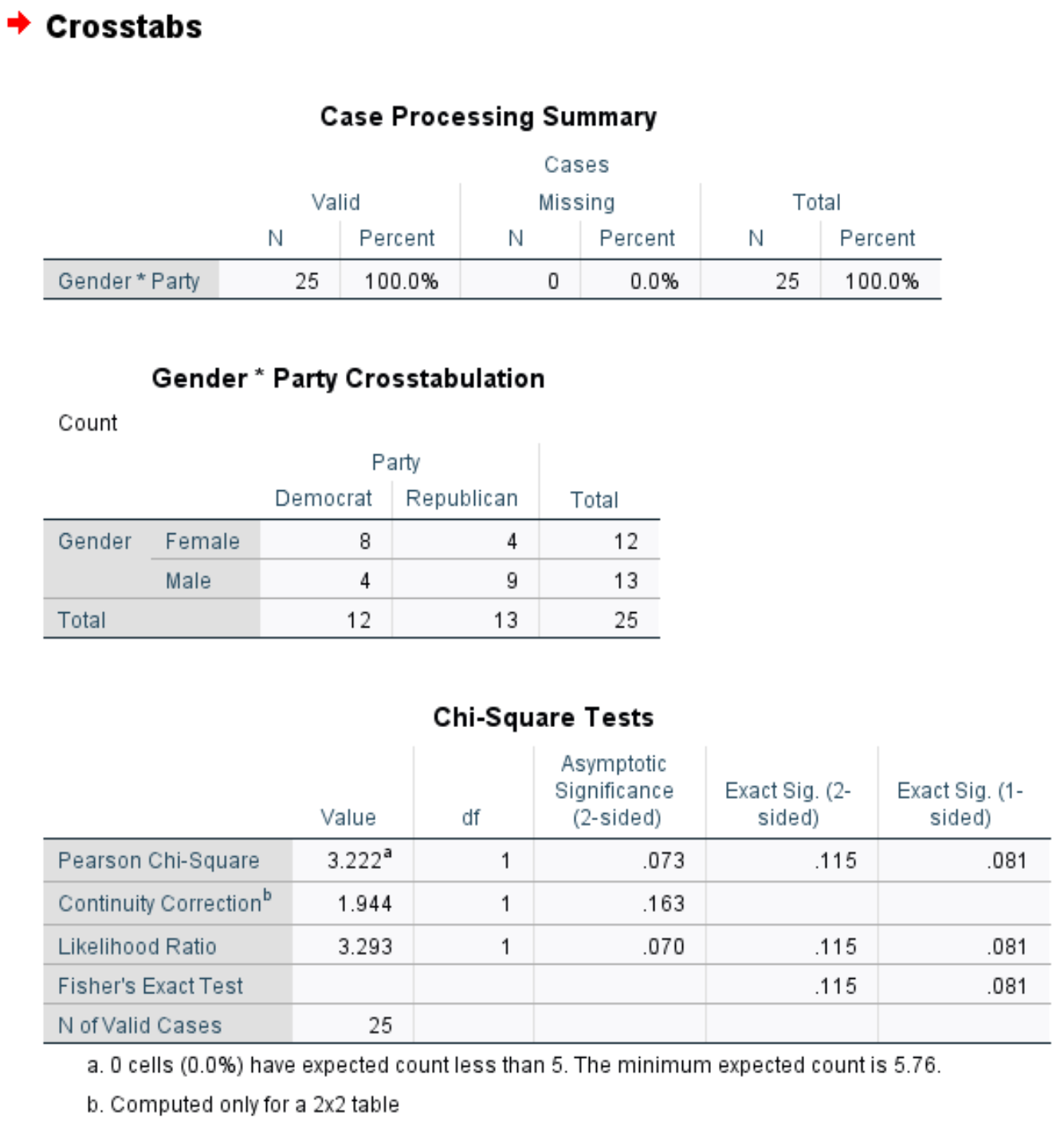
La prima tabella mostra il numero di casi mancanti nel set di dati. Possiamo vedere che in questo esempio ci sono 0 casi mancanti.
La seconda tabella presenta una tabella incrociata del numero totale di individui per genere e preferenza di partito politico.
La terza tabella mostra i risultati del test esatto di Fisher. Possiamo vedere i seguenti due valori p per il test:
- Valore p bilaterale: 0,115
- Valore p unilaterale: 0,081
L’ipotesi nulla del test esatto di Fisher è che le due variabili siano indipendenti. In questo caso, la nostra ipotesi nulla è che il genere e la preferenza del partito politico siano indipendenti, che è un test a due code, quindi utilizzeremmo il valore p a due code di 0,115.
Poiché questo valore p non è inferiore a 0,05, non rifiutiamo l’ipotesi nulla. Pertanto non abbiamo prove sufficienti per affermare che esista un’associazione significativa tra genere e preferenza del partito politico.