Che cos'è una statistica test standardizzata?
Un’ipotesi statistica è un’ipotesi relativa a un parametro della popolazione . Ad esempio, possiamo supporre che l’altezza media di un uomo negli Stati Uniti sia di 70 pollici. L’ipotesi relativa all’altezza è l’ ipotesi statistica e la vera altezza media di un uomo negli Stati Uniti è il parametro della popolazione .
Un test di ipotesi è un test statistico formale che utilizziamo per rifiutare o non riuscire a rifiutare un’ipotesi statistica.
Il processo di base per eseguire il test delle ipotesi è il seguente:
1. Raccogliere dati campione.
2. Calcolare la statistica del test standardizzato per i dati del campione.
3. Confrontare la statistica del test standardizzato con un valore critico. Se è più estremo del valore critico, rifiuta l’ipotesi nulla. Altrimenti non rifiutare il test dell’ipotesi nulla.
La formula che utilizziamo per calcolare la statistica del test standardizzato varia a seconda del tipo di test di ipotesi che stiamo eseguendo.
La tabella seguente mostra la formula da utilizzare per calcolare la statistica del test standardizzato per ciascuno dei quattro principali tipi di test di ipotesi:
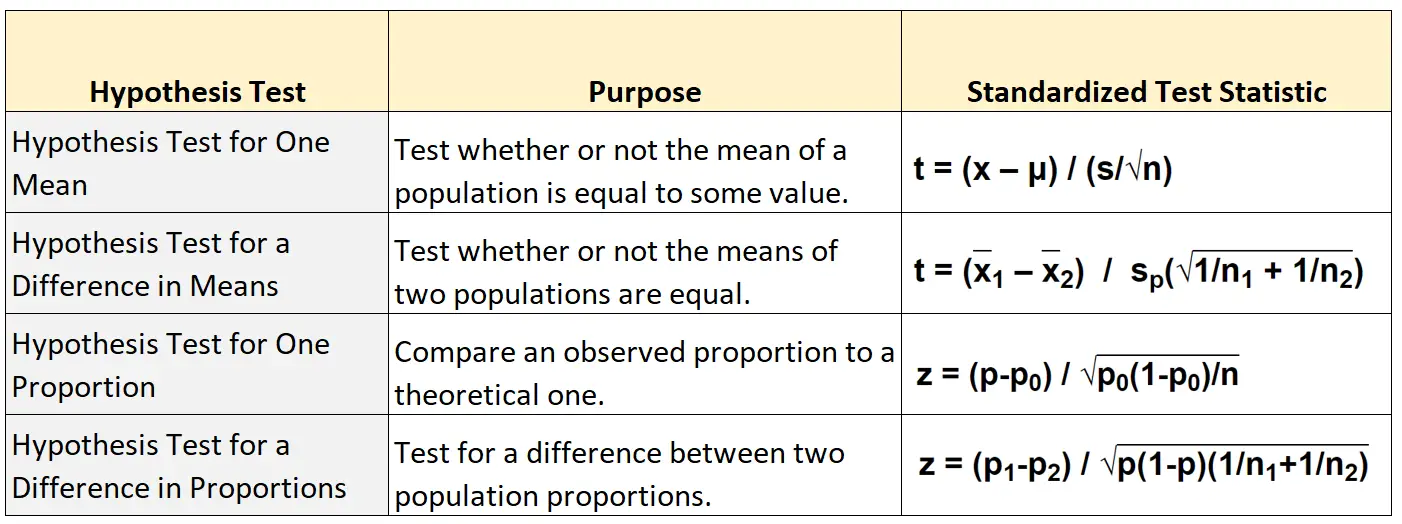
Verifica di ipotesi per una media
Un test t su un campione viene utilizzato per verificare se la media di una popolazione è uguale o meno a un determinato valore.
La statistica del test standardizzato per questo tipo di test viene calcolata come segue:
t = ( X – μ) / (s/√n)
Oro:
- x: media campionaria
- μ 0 : media ipotetica della popolazione
- s: deviazione standard campionaria
- n: dimensione del campione
Fare riferimento a questo tutorial per un esempio di calcolo di questa statistica di test standardizzato.
Verifica di ipotesi per una differenza nelle medie
Un t-test a due campioni viene utilizzato per verificare se le medie di due popolazioni sono uguali o meno.
La statistica del test standardizzato per questo tipo di test viene calcolata come segue:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
dove x 1 e x 2 sono le medie campionarie, n 1 e n 2 sono le dimensioni del campione e dove s p è calcolato come segue:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
dove s 1 2 e s 2 2 sono le varianze campionarie.
Fare riferimento a questo tutorial per un esempio di calcolo di questa statistica di test standardizzato.
Verifica di ipotesi per una proporzione
Un test z su una proporzione viene utilizzato per confrontare una proporzione osservata con una proporzione teorica.
La statistica del test standardizzato per questo tipo di test viene calcolata come segue:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
Oro:
- p: proporzione campionaria osservata
- p 0 : proporzione ipotetica della popolazione
- n: dimensione del campione
Fare riferimento a questo tutorial per un esempio di calcolo di questa statistica di test standardizzato.
Verifica di ipotesi per una differenza di proporzioni
Un test z a due proporzioni viene utilizzato per verificare la differenza tra due proporzioni della popolazione.
La statistica del test standardizzato per questo tipo di test viene calcolata come segue:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
dove p 1 e p 2 sono le proporzioni del campione, n 1 e n 2 sono le dimensioni del campione e dove p è la proporzione totale aggregata calcolata come segue:
p = ( p1n1 + p2n2 )/ ( n1 + n2 )
Fare riferimento a questo tutorial per un esempio di calcolo di questa statistica di test standardizzato.
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più