Come eseguire manualmente un test t accoppiato

Un test t per campioni accoppiati viene utilizzato per confrontare le medie di due campioni quando ciascuna osservazione in un campione può essere associata a un’osservazione nell’altro campione.

Il seguente esempio passo passo mostra come eseguire un test t per campioni accoppiati per determinare se le medie della popolazione sono uguali tra i due gruppi seguenti:

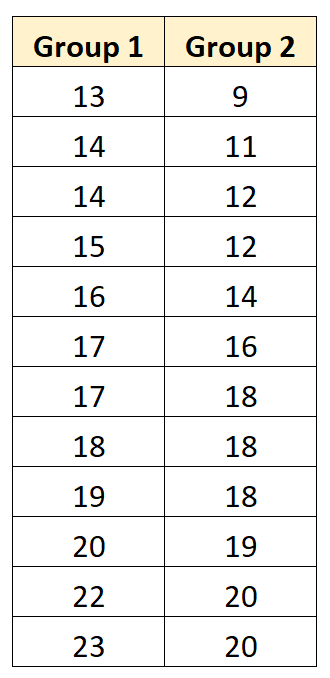
Passaggio 1: calcolare la statistica del test

La statistica del test di un t-test appaiato viene calcolata come segue:

t = x _diff / (s _diff /√ n )

Oro:

• x _diff : esempio di media delle differenze
• s: esempio di deviazione standard delle differenze
• n: dimensione del campione (ovvero numero di coppie)

Calcoleremo la media delle differenze tra i due gruppi e la deviazione standard delle differenze tra i due gruppi:

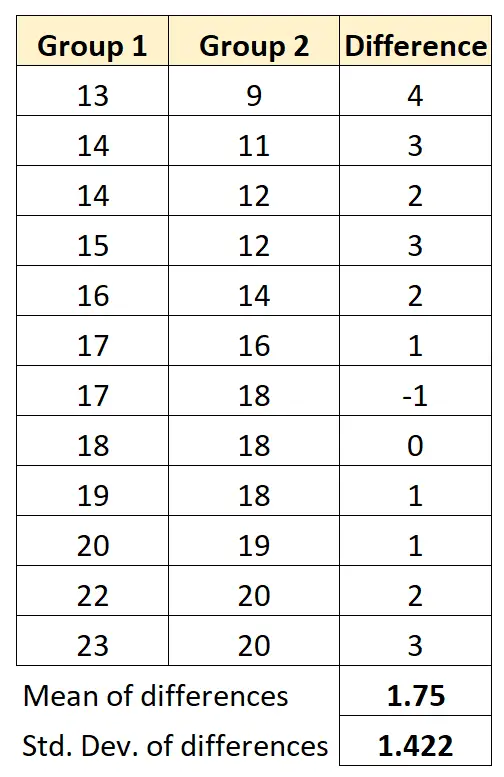
Pertanto, la nostra statistica test può essere calcolata come segue:

• t = x _diff / (s _diff /√ n )
• t = 1,75 / (1,422/√ 12 )
• t = 4,26

Passaggio 2: calcolare il valore critico

Successivamente, dobbiamo trovare il valore critico con cui confrontare le nostre statistiche di test.

Per questo esempio utilizzeremo un test a due code con α = 0,05 e df = n-1 gradi di libertà.

Secondo la tabella della distribuzione t, il valore critico che corrisponde a questi valori è 2.201 :

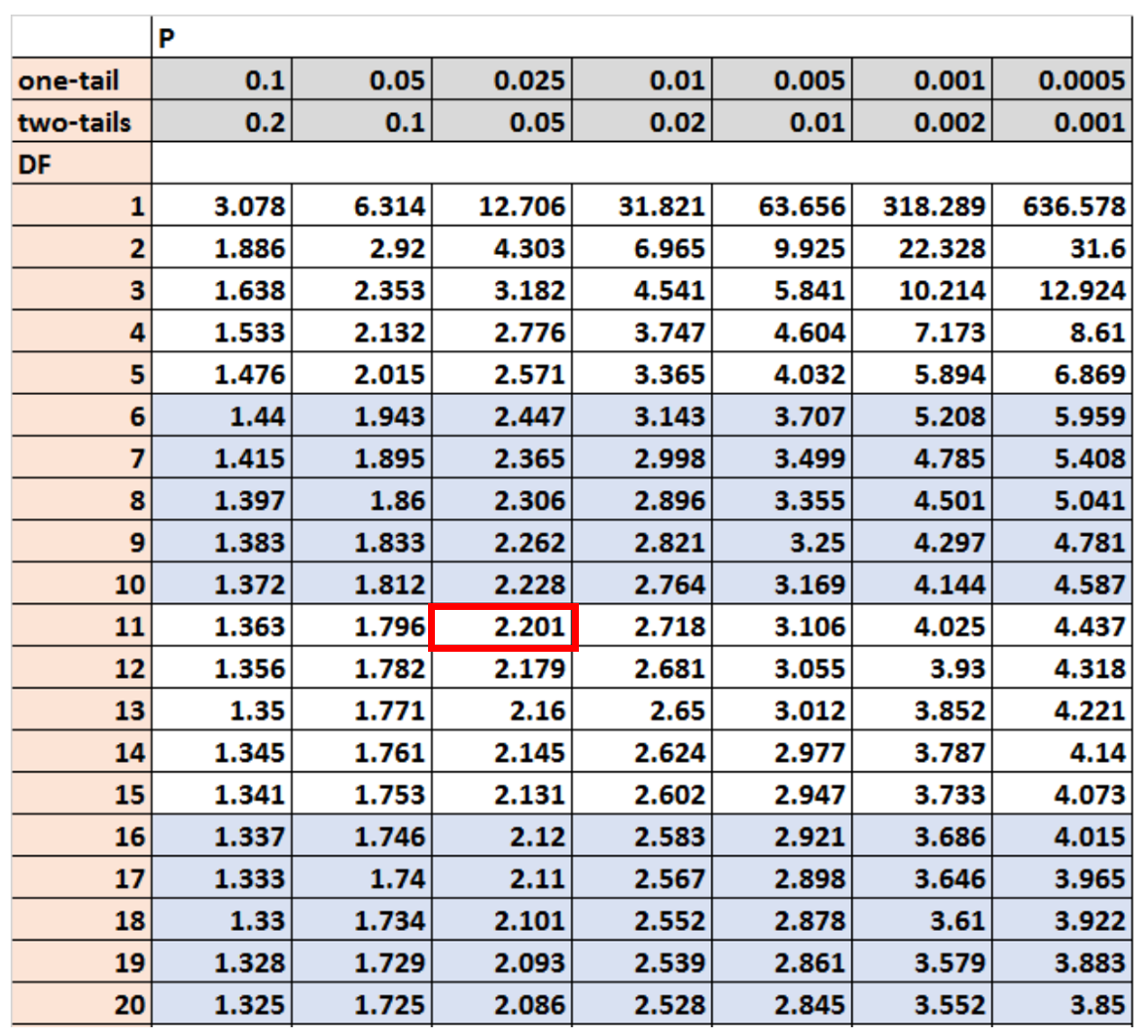
Passaggio 3: rifiutare o non riuscire a rifiutare l’ipotesi nulla

Il nostro t-test per campioni accoppiati utilizza la seguente ipotesi nulla e alternativa:

• H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)
• H _A : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Poiché il valore assoluto della nostra statistica test ( 4,26 ) è maggiore del valore critico trovato nella tabella t ( 2,201 ), rifiutiamo l’ipotesi nulla.

Ciò significa che abbiamo prove sufficienti per affermare che la media tra i due gruppi non è uguale.

Bonus: sentiti libero di utilizzare il calcolatore del test t dei campioni accoppiati per confermare i risultati.