T-test per campioni accoppiati: definizione, formula ed esempio

Un test t per campioni accoppiati viene utilizzato per confrontare le medie di due campioni quando ciascuna osservazione in un campione può essere associata a un’osservazione nell’altro campione.

Questo tutorial spiega quanto segue:

• La motivazione per eseguire un t-test per campioni appaiati.
• La formula per eseguire un test t per campioni accoppiati.
• I presupposti che devono essere soddisfatti per eseguire un t-test per campioni appaiati.
• Un esempio di come eseguire un t-test per campioni accoppiati.

Test t per campioni accoppiati: motivazione

Un t-test per campioni appaiati viene comunemente utilizzato in due scenari:

1. Viene effettuata una misurazione su un soggetto prima e dopo un trattamento – ad esempio, il salto verticale massimo dei giocatori di basket universitari viene misurato prima e dopo la loro partecipazione a un programma di allenamento.

2. Una misurazione viene effettuata in due condizioni diverse : ad esempio, il tempo di risposta di un paziente viene misurato con due farmaci diversi.

In entrambi i casi, vogliamo confrontare la misurazione media tra due gruppi in cui ciascuna osservazione di un campione può essere associata a un’osservazione dell’altro campione.

Test t per campioni accoppiati: formula

Un t-test per campioni appaiati utilizza sempre la seguente ipotesi nulla:

• H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)

L’ipotesi alternativa può essere bilaterale, sinistra o destra:

• H ₁ (a due code): μ ₁ ≠ μ ₂ (le medie delle due popolazioni non sono uguali)
• H ₁ (a sinistra): μ ₁ < μ ₂ (la media della popolazione 1 è inferiore alla media della popolazione 2)
• H ₁ (a destra): μ ₁ > μ ₂ (la media della popolazione 1 è maggiore della media della popolazione 2)

Usiamo la seguente formula per calcolare la statistica del test t:

t = x _diff / (s _diff /√n)

Oro:

• x _diff : esempio di media delle differenze
• s: esempio di deviazione standard delle differenze
• n: dimensione del campione (ovvero numero di coppie)

Se il valore p che corrisponde alla statistica t-test con (n-1) gradi di libertà è inferiore al livello di significatività scelto (le scelte comuni sono 0,10, 0,05 e 0,01), è possibile rifiutare l’ipotesi nulla.

T-test per campioni appaiati: ipotesi

Affinché i risultati di un t-test per campioni appaiati siano validi, devono essere soddisfatte le seguenti ipotesi:

• I partecipanti dovrebbero essere selezionati in modo casuale dalla popolazione.
• Le differenze tra le coppie dovrebbero essere distribuite approssimativamente normalmente.
• Non dovrebbero esserci valori anomali estremi nelle differenze.

Test t per campioni accoppiati : esempio

Supponiamo di voler sapere se un determinato programma di allenamento è in grado o meno di aumentare il salto verticale massimo (in pollici) dei giocatori di basket universitari.

Per verificarlo, possiamo reclutare un semplice campione casuale di 20 giocatori di basket universitari e misurare ciascuno dei loro salti verticali massimi. Successivamente possiamo far utilizzare a ciascun giocatore il programma di allenamento per un mese e poi misurare nuovamente il salto verticale massimo alla fine del mese.

Per determinare se il programma di allenamento ha effettivamente avuto un effetto sul salto verticale massimo, eseguiremo un t-test per campioni appaiati al livello di significatività α = 0,05 utilizzando i seguenti passaggi:

Passaggio 1: calcolare i dati di riepilogo per le differenze.

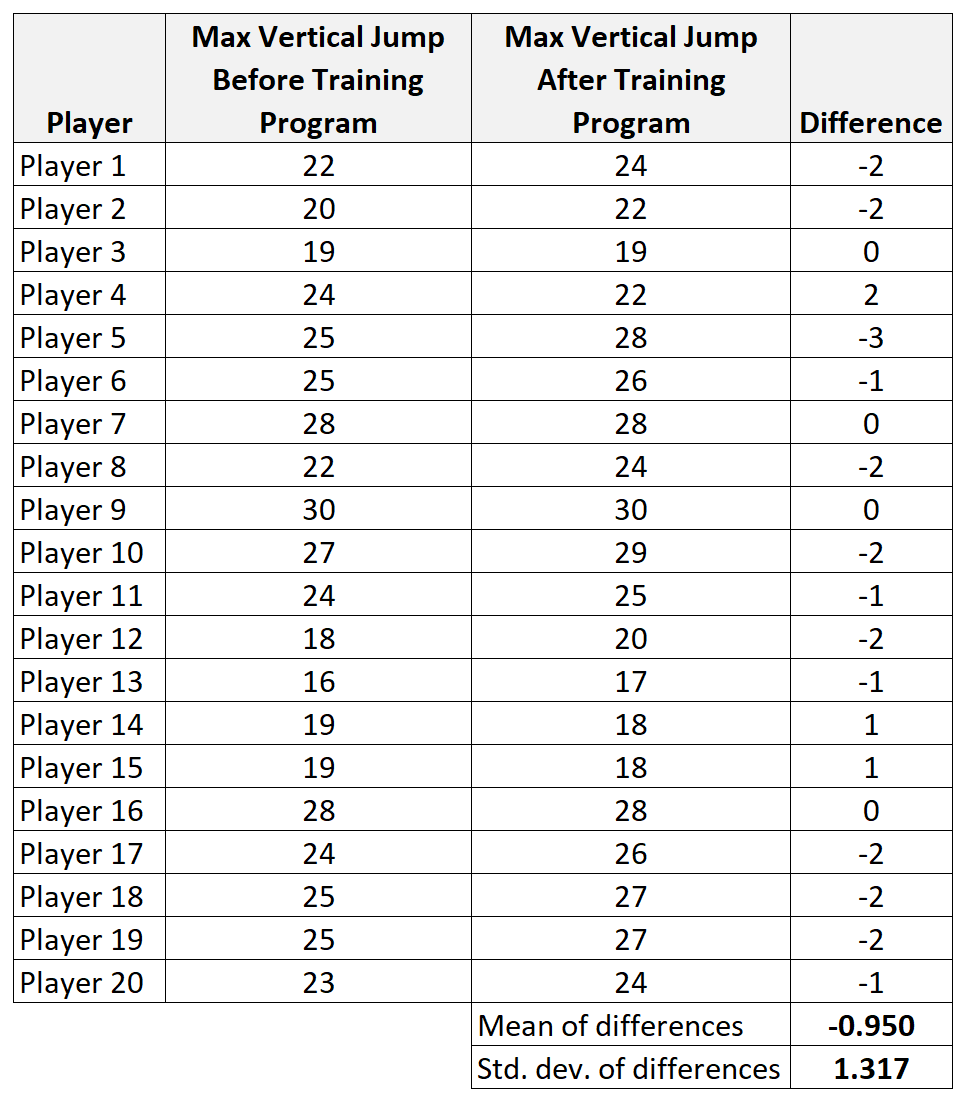
• x _diff : media campionaria delle differenze = -0,95
• s: deviazione standard campionaria delle differenze = 1.317
• n: dimensione del campione (ovvero numero di coppie) = 20

Passaggio 2: definire le ipotesi.

Effettueremo il t-test per campioni appaiati con le seguenti ipotesi:

• H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)
• H ₁ : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Passaggio 3: calcolare la statistica t -test.

t = x _diff / (s _diff /√n) = -0,95 / (1,317/ √ 20) = -3,226

Passaggio 4: calcolare il valore p della statistica t- test.

Secondo il calcolatore del punteggio T al valore P , il valore p associato a t = -3,226 e gradi di libertà = n-1 = 20-1 = 19 è 0,00445 .

Passaggio 5: trarre una conclusione.

Poiché questo valore p è inferiore al nostro livello di significatività α = 0,05, rifiutiamo l’ipotesi nulla. Abbiamo prove sufficienti per affermare che il salto verticale massimo medio dei giocatori è diverso prima e dopo la partecipazione al programma di allenamento.

Nota: è anche possibile eseguire l’intero test t per campioni appaiati semplicemente utilizzando il calcolatore del test t per campioni appaiati .

Risorse addizionali

I seguenti tutorial spiegano come eseguire un t-test per campioni appaiati utilizzando diversi programmi statistici:

Come eseguire un test t per campioni accoppiati in Excel
Come eseguire un t-test per campioni accoppiati in SPSS
Come eseguire un t-test per campioni accoppiati in Stata
Come eseguire un t-test per campioni accoppiati su una calcolatrice TI-84
Come eseguire un t-test per campioni accoppiati in R
Come eseguire un t-test di campioni accoppiati in Python
Come eseguire manualmente un test T su campioni accoppiati