Tipi medi (statistiche)

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

Qui spieghiamo cosa sono tutti i tipi di medie nelle statistiche e come vengono calcolati. Troverai la formula per ogni tipologia di calza ed esempi.

Ma prima di vedere quali sono i tipi di media, dobbiamo logicamente sapere cos’è una media in statistica. Ti consigliamo pertanto di consultare il seguente link prima di proseguire.

➤ Vedi: Qual è la media (statistica)?

Quali sono i tipi di medie nelle statistiche?

In statistica, i tipi di medie sono:

Media aritmetica
Media ponderata
Mezzi geometrici
radice significa quadrato
significato armonico
media generalizzata
media f generalizzata
mezzi tagliati
media interquartile
media di una funzione

Successivamente spiegheremo come calcolare tutti i tipi di medie nelle statistiche. I cinque tipi di media più comunemente utilizzati sono la media aritmetica, la media ponderata, la media geometrica, la media quadratica e la media armonica. Quindi entreremo più in dettaglio su questi cinque principali tipi di media.

Media aritmetica

La media aritmetica viene calcolata sommando tutti i valori e quindi dividendo per il numero totale di punti dati.

La formula della media aritmetica è quindi la seguente:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

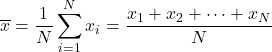
La media aritmetica è detta anche media aritmetica .

La media aritmetica è probabilmente il tipo di media più utilizzato in statistica.

Per vedere un esempio di come si ottiene questo tipo di media, calcoleremo la media aritmetica dei seguenti dati:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Per calcolare la media aritmetica, somma semplicemente tutti i dati statistici e dividi per il numero totale di dati, che è 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Media ponderata

Per calcolare la media ponderata, è necessario prima moltiplicare ciascun dato statistico per il suo peso (o peso), quindi sommare tutti i prodotti e infine dividere la somma ponderata per la somma di tutti i pesi.

La formula della media ponderata è quindi la seguente:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

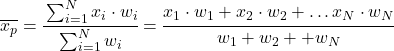
Dove x _i è il valore statistico e w _i il suo peso corrispondente.

La media ponderata è più difficile da comprendere, quindi ti consigliamo di consultare il seguente esempio che spiega passo dopo passo come viene calcolata:

➤ Vedi: Esempio di media ponderata

Mezzi geometrici

La media geometrica di un insieme di dati statistici è uguale alla radice n-esima del prodotto di tutti i valori.

Questo tipo di media viene utilizzato nella finanza aziendale per calcolare i tassi di rendimento, le medie percentuali e gli interessi composti.

La formula per questo tipo di archiviazione è piuttosto complicata. In effetti, la media geometrica di tutti gli insiemi statistici non può essere calcolata, ma a volte questo tipo di media non può essere determinata. Per questo motivo ti consigliamo di consultare tutte le eccezioni spiegate nel seguente link:

➤ Vedi: formula della media geometrica

radice significa quadrato

La radice quadrata media è uguale alla radice quadrata della media aritmetica dei quadrati dei dati.

La formula del valore quadratico medio è quindi la seguente:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Questo tipo di media è anche chiamato radice quadrata media , radice quadrata media o RMS .

Facciamo solo notare che esiste anche la media cubica, ma viene utilizzata in casi molto particolari.

La media quadrata presenta vantaggi e svantaggi, ad esempio è particolarmente utile quando la variabile statistica assume valori positivi e negativi, perché elevando al quadrato ogni dato, tutti i valori diventano positivi. Puoi vedere più funzionalità di questo tipo di media facendo clic sul seguente collegamento:

➤ Vedi: vantaggi e svantaggi della radice quadrata media

significato armonico

La media armonica viene calcolata dividendo il numero totale di dati statistici per la somma dei reciproci di ciascun valore.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

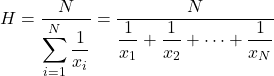
La media armonica viene utilizzata per calcolare velocità medie, tempi o effettuare calcoli elettronici. Questa caratteristica differenzia la media armonica da altri tipi di medie, frequentemente utilizzate nel calcolo delle medie o delle percentuali dei prezzi.

Puoi vedere esempi di calcolo di questo tipo di media nella pagina seguente:

➤ Vedi: esempi di significato armonico

Altri tipi di calze

In questa sezione vedremo le formule per altri tipi di calze. Non entreremo nei dettagli di ciascuna tipologia perché non sono molto utilizzate, ma è bene sapere che esistono altri tipi di calze.

La media generalizzata è una combinazione dei tipi medi visti sopra e viene calcolata utilizzando la seguente formula:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

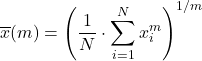
Sia f una funzione iniettiva e monotona, quindi la media f generalizzata definita come:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

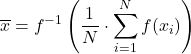
La media troncata prevede il calcolo della media aritmetica dopo aver sottratto una percentuale di osservazioni alle estremità superiore e inferiore del campione. La stessa percentuale dovrebbe essere respinta da entrambe le parti.

Per calcolare la media interquartile , detta anche media interquartile, vengono prima scartati i dati del primo e del quarto quartile, quindi viene calcolata solo la media aritmetica del secondo e del terzo quartile del campione. La formula per questo tipo di media è quindi:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

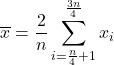
Infine, puoi anche trovare la media di una funzione . Il valore medio di una funzione continua su un intervallo chiuso [a,b] si calcola utilizzando la seguente formula:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Media campionaria e della popolazione

Infine vedremo qual è la differenza tra la media campionaria e la media della popolazione, due tipologie di medie che spesso vengono confuse.

La media campionaria è la media calcolata sui valori di un campione statistico, ovvero viene calcolata su una parte di tutti i valori di una variabile.

La media della popolazione è la media calcolata su una popolazione statistica, cioè su tutti i valori di una variabile. Pertanto, la media della popolazione coincide con l’aspettativa matematica della variabile.

La media campionaria può essere considerata praticamente uguale alla media della popolazione se è nota una quantità di dati sufficientemente ampia. Ma il valore della media della popolazione è molto difficile da ottenere, poiché in realtà tutti i valori di una distribuzione sono raramente conosciuti.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più