Digitando

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cosa significa caratterizzare una distribuzione in statistica. Troverai così la definizione di tipizzazione, un esempio di tipizzazione di una variabile e, inoltre, potrai esercitarti con un esercizio risolto passo dopo passo.

Cos’è la digitazione?

In statistica, la normalizzazione è un processo in cui una trasformazione lineare viene applicata a una distribuzione in modo tale che la sua media e deviazione standard siano pari rispettivamente a zero e uno.

Più precisamente, la tipizzazione comporta la sottrazione della media dalla variabile casuale e la divisione per la deviazione standard.

La digitazione può anche essere chiamata normalizzazione o standardizzazione.

Inserisci la formula

Per classificare una variabile è necessario sottrarre la sua media e poi dividerla per la sua deviazione standard. La formula per inserire una variabile è quindi la seguente:

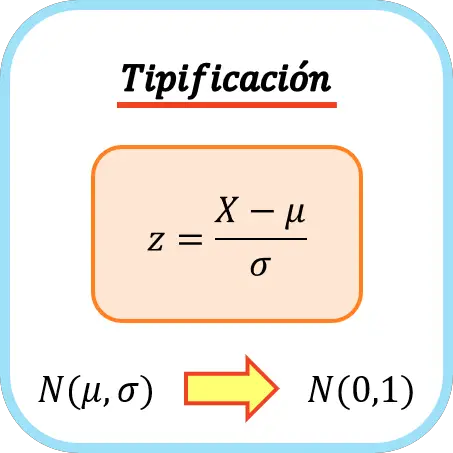
Oro

$\mu$

è la media della variabile

$X$

$\sigma$

la sua deviazione standard (o deviazione standard).

Pertanto, l’immissione è in realtà una modifica della variabile, poiché alla variabile viene applicata una trasformazione lineare.

Voce di esempio

Considerando la definizione di tipizzazione e la sua formula, di seguito è riportato un esempio concreto per comprendere appieno il concetto.

Una variabile casuale continua segue una distribuzione normale con media 45 e deviazione standard 10, qual è la probabilità di ottenere un valore inferiore o uguale a 60?

$N(45,10)$

Per trovare la probabilità di una distribuzione normale dobbiamo utilizzare la sua tabella caratteristica, ma per fare ciò dobbiamo prima eseguire il processo di tipizzazione. Quindi sottraiamo la media e dividiamo per la deviazione standard per il valore di probabilità:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Una volta standardizzata, passiamo alla tabella di probabilità della distribuzione normale per vedere a quale probabilità corrisponde il valore di 1,5:

Come si può vedere nella tabella di tipizzazione della distribuzione normale, il valore calcolato nel passaggio precedente corrisponde alla seguente probabilità:

$\displaystyle P(Z\leq 1,5)=0,9332$

La probabilità di ottenere un valore uguale o inferiore a 60 è quindi del 93,32%.

Esercizio di digitazione risolto

Calcola le seguenti probabilità di una distribuzione normale la cui media e deviazione standard sono rispettivamente 120 e 50.

$N(120,50)$

La probabilità di ottenere un valore inferiore o uguale a 208.
La probabilità di ottenere un valore maggiore di 137.

Vedi la soluzione

In entrambe le sezioni del problema, dobbiamo digitare la distribuzione normale per calcolare le probabilità.

Iniziamo calcolando la probabilità di battitura di un valore inferiore o equivalente a 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

E ora guardiamo la tabella qui sopra a quale probabilità corrisponde il valore 1,76:

$\displaystyle P(Z\leq 1,76)=0,9608$

In secondo luogo, calcoleremo la probabilità di ottenere un valore maggiore di 137. Allo stesso modo, inizieremo digitando la variabile:

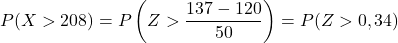$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ Tuttavia, la tabella allegata ha solo le probabilità cumulative più basse, quindi per utilizzare la tabella dobbiamo prima trasformare la probabilità:

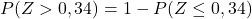$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ E, infine, noteremo dalla tabella allegata la probabilità corrispondente al valore calcolato di Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

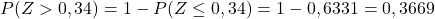
Qual è lo scopo di digitare?

Per finire di comprendere il significato della tipizzazione, vedremo a cosa serve e quando deve essere digitata una variabile.

Principalmente, la standardizzazione viene utilizzata per confrontare i valori delle distribuzioni con medie e varianze diverse. Allo stesso modo, la standardizzazione viene utilizzata anche per calcolare una probabilità.

Standardizzando due valori di distribuzioni con caratteristiche diverse, possiamo vedere quale valore è maggiore o minore rispetto all’intera distribuzione. O in altre parole, applicando il processo di tipizzazione, possiamo vedere quale valore è più vicino o più lontano dalla media della sua distribuzione.

Inoltre, come spiegato sopra, la tipizzazione consente anche il calcolo delle probabilità, poiché generalmente le tabelle di probabilità si basano su una distribuzione tipizzata.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più