Che cos'è un complotto di bland-altman? (definizione & #038; esempio)

Un diagramma di Bland-Altman viene utilizzato per visualizzare le differenze di misurazione tra due diversi strumenti o due diverse tecniche di misurazione.

Viene spesso utilizzato per valutare la somiglianza di un nuovo strumento o tecnica per misurare qualcosa con lo strumento o la tecnica attualmente in uso.

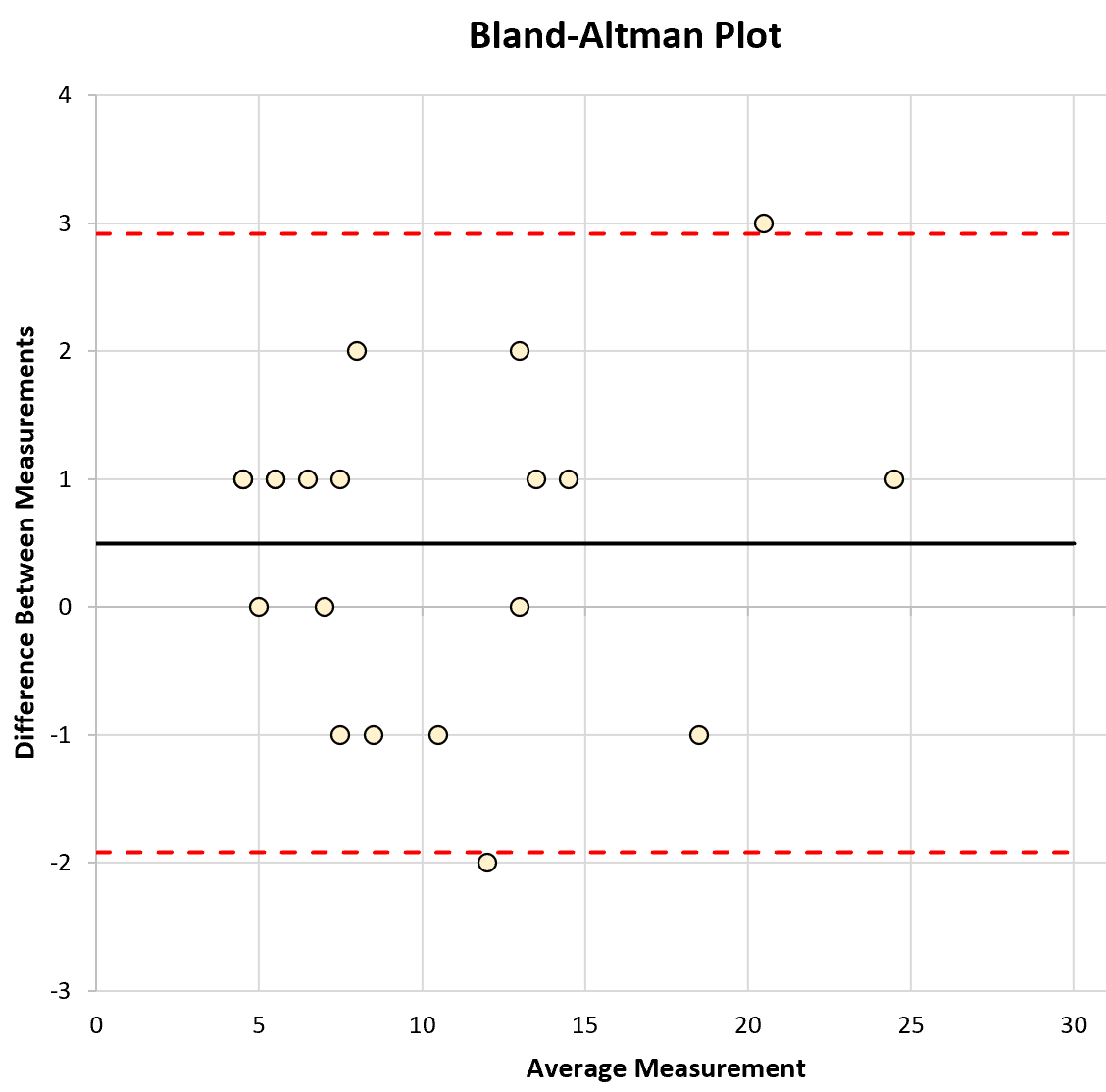
L’asse x del grafico mostra la misurazione media dei due strumenti e l’asse y mostra la differenza nelle misurazioni tra i due strumenti.

Nella trama vengono visualizzate anche le tre righe seguenti:

• La differenza media nelle misurazioni tra i due strumenti
• Il limite superiore dell’intervallo di confidenza al 95% per la differenza media
• Il limite inferiore dell’intervallo di confidenza al 95% per la differenza media

Questo tipo di trama è utile per determinare due cose:

1. Qual è la differenza media nelle misurazioni tra i due strumenti?

La linea orizzontale tracciata al centro del grafico mostra la differenza media nelle misurazioni tra i due strumenti. Questo valore viene spesso definito “bias” tra gli strumenti.

Quanto più questo valore è lontano da zero, tanto maggiore è la differenza media nelle misurazioni tra gli strumenti.

2. Qual è il tipico range di accordo tra i due strumenti?

Le linee dell’intervallo di confidenza superiore e inferiore ci danno un’idea del tipico range di accordo tra i due strumenti. In generale, il 95% delle differenze tra i due strumenti rientra in questi limiti di confidenza.

Più ampio è l’intervallo di confidenza, maggiore è il range delle differenze di misurazione tra i due strumenti.

Il seguente esempio passo passo mostra come creare e interpretare da zero un grafico Bland-Altman.

Nota: un grafico di Bland-Altman è talvolta chiamato grafico delle differenze medie di Tukey. Questi nomi sono usati in modo intercambiabile.

Passaggio 1: raccogliere i dati

Supponiamo che un biologo voglia sapere quanto sono simili due diversi strumenti per misurare il peso delle rane, in grammi. Usa due strumenti (A e B) per pesare lo stesso set di 20 rane.

Il peso dei nasetti, misurato da ciascuno strumento, è riportato nella tabella seguente:

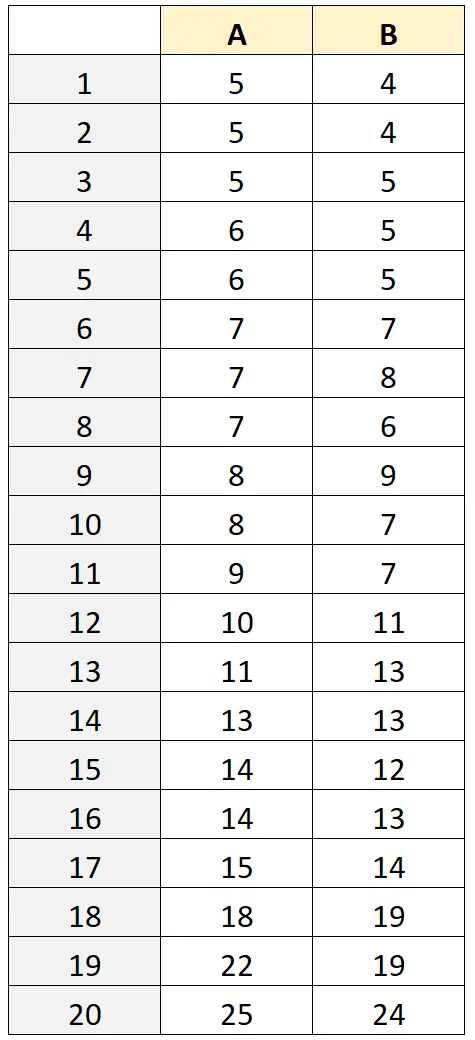
Passaggio 2: calcolare la misurazione media e la differenza delle misurazioni

Successivamente, calcoleremo la misura media ((A+B)/2) e la differenza nelle misure (AB) per ciascuna rana:

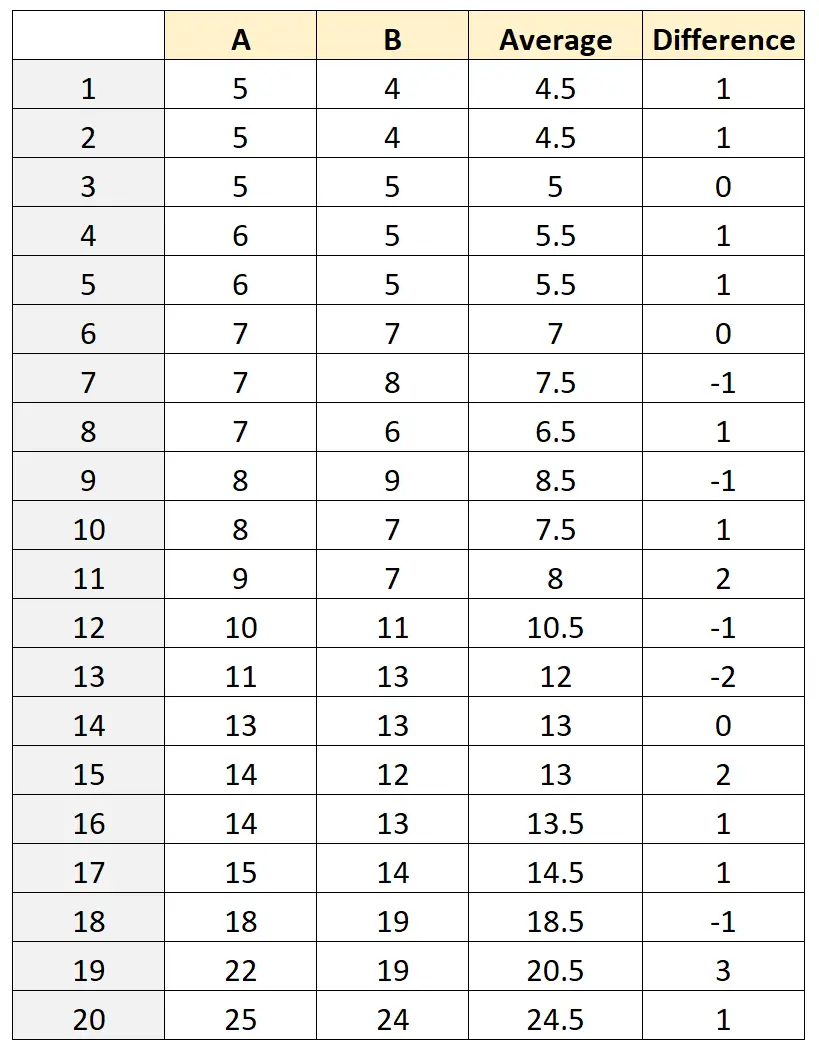
Passaggio 3: calcolare la differenza media e l’intervallo di confidenza

La media dei valori nella colonna Differenza risulta essere 0,5 .

La deviazione standard dei valori nella colonna Differenza risulta essere 1.235 .

I limiti superiore e inferiore dell’intervallo di confidenza per la differenza media possono essere calcolati come segue:

Limite superiore: x + 1,96*s = 0,5 + 1,96*1,235 = 2,92

Limite inferiore: x – 1,96*s = 0,5 – 1,96*1,235 = -1,92

Ecco come interpretare questi valori:

• In media lo strumento A pesa 0,5 grammi in più rispetto allo strumento B.
• Il 95% delle differenze di peso tra i due strumenti dovrebbe essere compreso tra -1,92 grammi e 2,92 grammi.

Successivamente, creeremo un grafico Bland-Altman per visualizzare questi valori.

Passaggio 4: crea la trama

Quindi possiamo creare il grafico seguente che mostra la misura media dei due strumenti sull’asse x e la differenza tra le misure sull’asse y.

Possiamo anche aggiungere una linea orizzontale alla differenza media tra le misurazioni (0,5), nonché un limite di confidenza superiore (2,92) e un limite di confidenza inferiore (-1,92) che abbiamo calcolato nel passaggio precedente:

Risorse addizionali

Come creare un grafico Bland-Altman in Excel
Come creare un grafico di Bland-Altman in R
Come creare un grafico Bland-Altman in Python