Come disegnare una curva roc in python (passo dopo passo)

La regressione logistica è un metodo statistico che utilizziamo per adattare un modello di regressione quando la variabile di risposta è binaria. Per valutare quanto bene un modello di regressione logistica si adatta a un set di dati, possiamo esaminare i due parametri seguenti:

• Sensibilità: probabilità che il modello preveda un risultato positivo per un’osservazione quando il risultato è effettivamente positivo. Questo è anche chiamato il “vero tasso positivo”.
• Specificità: la probabilità che il modello preveda un risultato negativo per un’osservazione quando il risultato è effettivamente negativo. Questo è anche chiamato “vero tasso negativo”.

Un modo per visualizzare queste due misurazioni è creare una curva ROC , che sta per curva “caratteristica operativa del ricevitore”. Questo è un grafico che mostra la sensibilità e la specificità di un modello di regressione logistica.

Il seguente esempio passo passo mostra come creare e interpretare una curva ROC in Python.

Passaggio 1: importa i pacchetti necessari

Per prima cosa importeremo i pacchetti necessari per eseguire la regressione logistica in Python:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Passaggio 2: adattare il modello di regressione logistica

Successivamente, importeremo un set di dati e adatteremo ad esso un modello di regressione logistica:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

Passaggio 3: traccia la curva ROC

Successivamente, calcoleremo il tasso di veri positivi e il tasso di falsi positivi e creeremo una curva ROC utilizzando il pacchetto di visualizzazione dei dati Matplotlib:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show () 

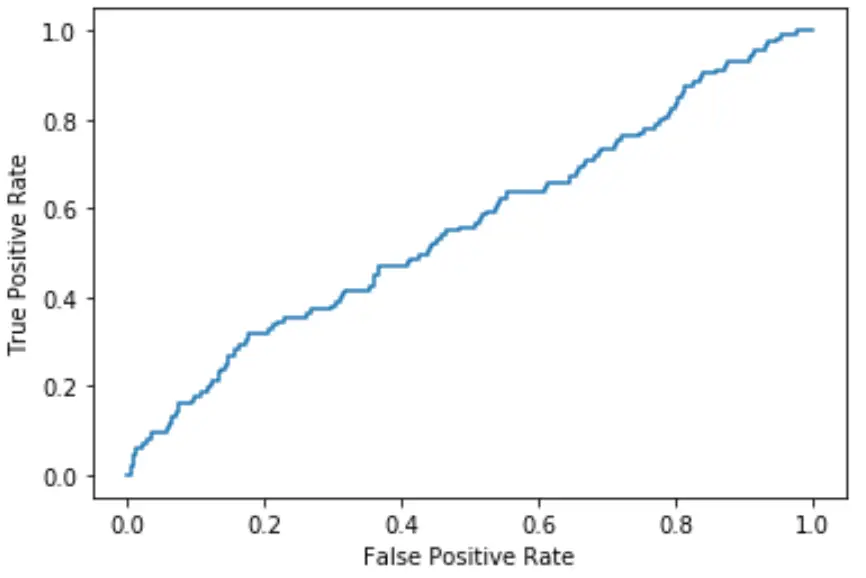
Quanto più la curva si avvicina all’angolo superiore sinistro del grafico, tanto meglio il modello è in grado di classificare i dati in categorie.

Come possiamo vedere dal grafico sopra, questo modello di regressione logistica fa un lavoro piuttosto scarso nell’ordinare i dati in categorie.

Per quantificarlo, possiamo calcolare l’AUC – area sotto la curva – che ci dice quanta parte del grafico si trova sotto la curva.

Più l’AUC è vicino a 1, migliore è il modello. Un modello con un’AUC pari a 0,5 non è migliore di un modello che esegue classificazioni casuali.

Passaggio 4: calcolare l’AUC

Possiamo utilizzare il seguente codice per calcolare l’AUC del modello e visualizzarlo nell’angolo in basso a destra del grafico ROC:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show () 

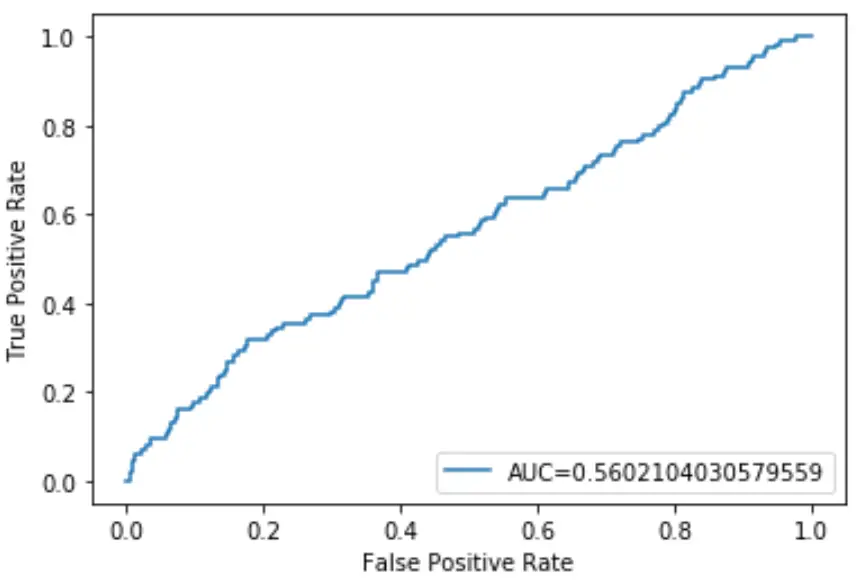
L’AUC di questo modello di regressione logistica risulta essere 0,5602 . Poiché questa cifra è vicina a 0,5, ciò conferma che il modello sta facendo un pessimo lavoro di classificazione dei dati.

Correlati: Come tracciare più curve ROC in Python