Cosa è considerato un complotto residuo buono o cattivo?

Nell’analisi di regressione, un grafico dei residui è un tipo di grafico che mostra i valori adattati di un modello di regressione sull’asse x e i residui del modello lungo l’asse y.

Quando ispezioniamo visivamente un layout residuo, generalmente cerchiamo due cose per determinare se il layout è “buono” o “cattivo”:

1. I residui mostrano un trend chiaro?

• In un diagramma dei residui “buono”, i residui non mostrano una tendenza chiara.
• In un grafico dei residui “cattivo”, i residui presentano un qualche tipo di schema, ad esempio una curva o un’onda. Ciò indica che il modello di regressione che abbiamo utilizzato non fornisce un adattamento appropriato ai dati.

2. I residui aumentano o diminuiscono sistematicamente nella varianza?

• In un diagramma dei residui “buono”, i residui sono sparsi casualmente intorno allo zero senza un aumento o una diminuzione sistematica della varianza.
• In un diagramma dei residui “cattivo”, la varianza dei residui aumenta o diminuisce sistematicamente.

Se un diagramma dei residui viene valutato “buono”, significa che possiamo fidarci dei risultati del modello di regressione e che è sicuro interpretare i coefficienti del modello.

Tuttavia, se un grafico dei residui viene classificato come “cattivo”, significa che i risultati del modello non sono affidabili e dobbiamo adattare ai dati un modello di regressione diverso.

Gli esempi seguenti spiegano come interpretare nella pratica i grafici dei residui “buoni” e “cattivi”.

Esempio 1: una traccia residua “buona”.

Supponiamo di adattare un modello di regressione e di ottenere il seguente diagramma dei residui:

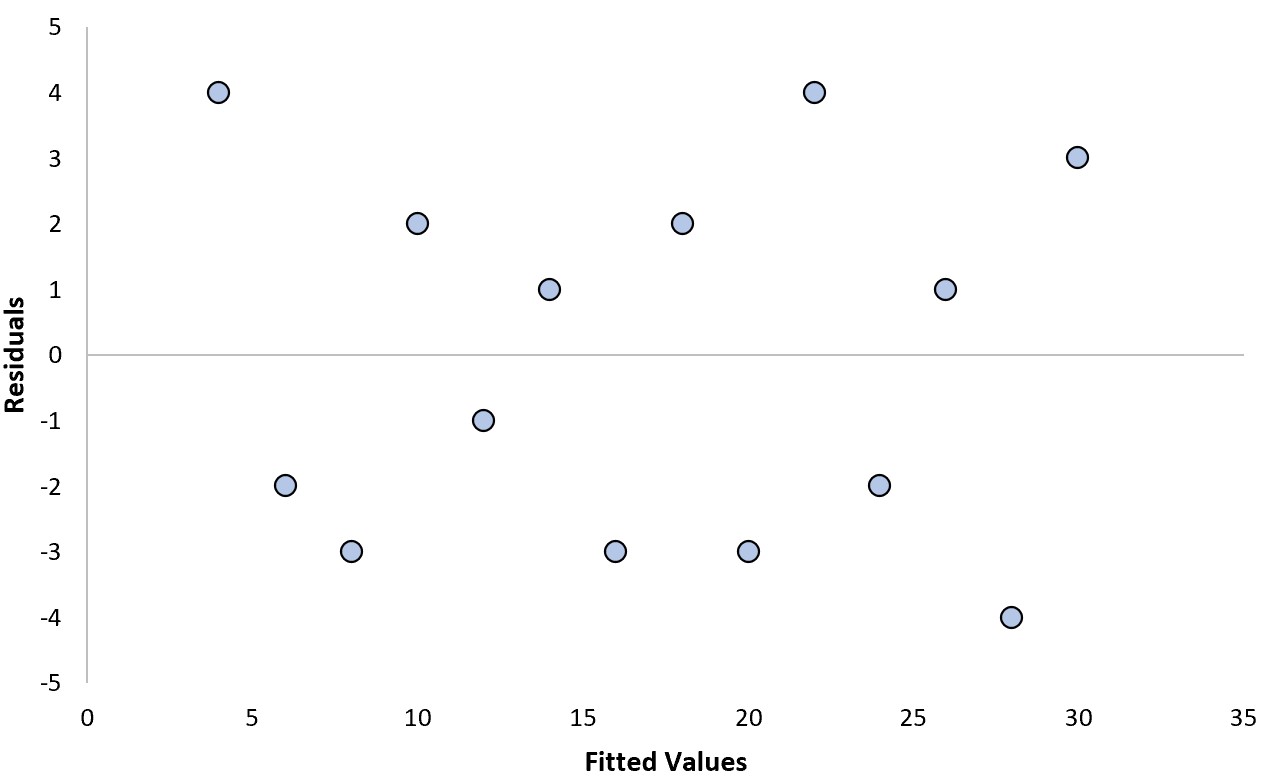
Possiamo rispondere alle seguenti due domande per determinare se si tratta di un diagramma residuo “buono”:

1. I residui mostrano un trend chiaro?

No. I residui sono sparsi in modo casuale attorno allo zero, senza uno schema chiaro.

2. I residui aumentano o diminuiscono sistematicamente nella varianza?

No. I residui hanno una varianza abbastanza costante (cioè la distanza tra i residui e il valore zero) a ciascun livello dei valori adattati.

Poiché abbiamo risposto “No” a entrambe le domande, considereremmo questa una trama residua “buona”.

Pertanto, possiamo fidarci dei risultati del modello di regressione e interpretare i coefficienti del modello in modo sicuro.

Esempio 2: una trama residua “cattiva” con un modello chiaro

Supponiamo di adattare un modello di regressione e di ottenere il seguente diagramma dei residui:

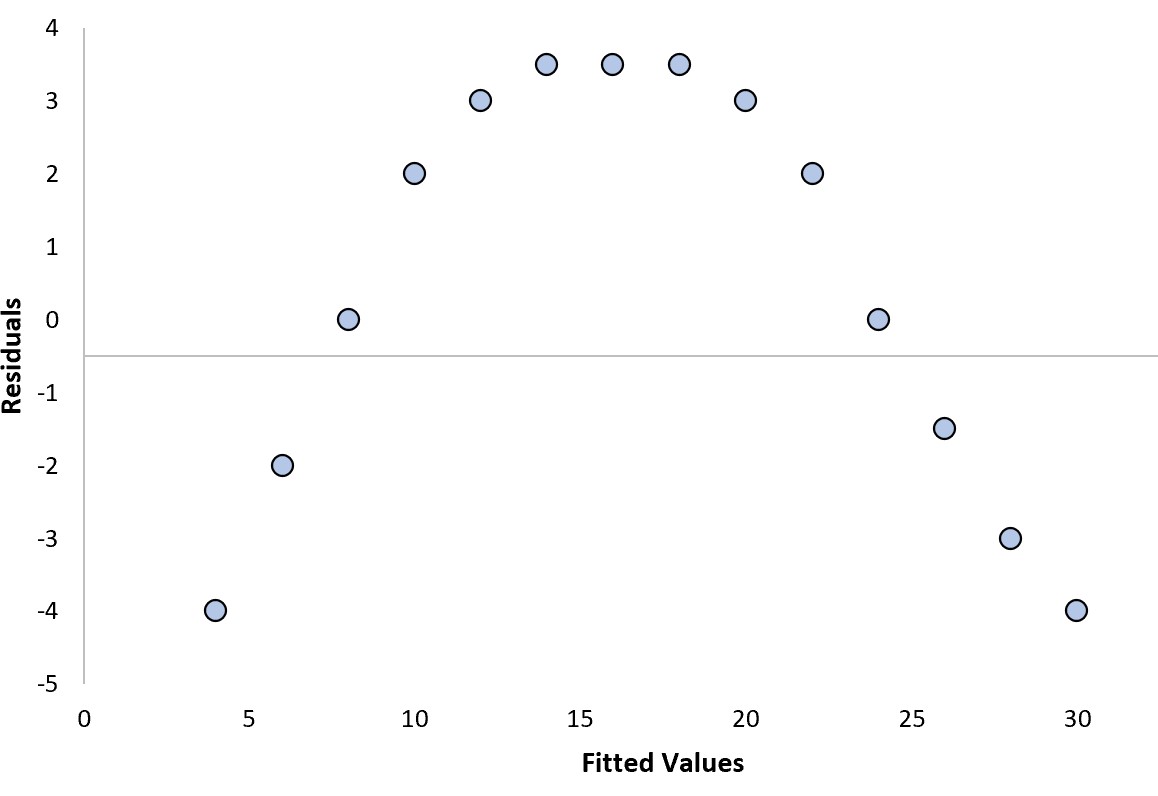
Possiamo rispondere alle seguenti due domande per determinare se si tratta di un diagramma residuo “buono”:

1. I residui mostrano un trend chiaro?

Sì . I residui mostrano un andamento curvo.

2. I residui aumentano o diminuiscono sistematicamente nella varianza?

Sì . I residui hanno diversi livelli di varianza a diversi livelli dei valori adattati.

Poiché abbiamo risposto “Sì” ad almeno una di queste domande, la considereremmo una trama residua “cattiva”.

Ciò significa che il modello di regressione non fornisce un buon adattamento ai dati.

In particolare, l’ andamento curvo nel grafico dei residui indica che un modello di regressione lineare non riesce ad adattare i dati e che un modello di regressione quadratica probabilmente farebbe un lavoro migliore.

Esempio 3: un diagramma residuo “cattivo” con varianza crescente

Supponiamo di adattare un modello di regressione e di ottenere il seguente diagramma dei residui:

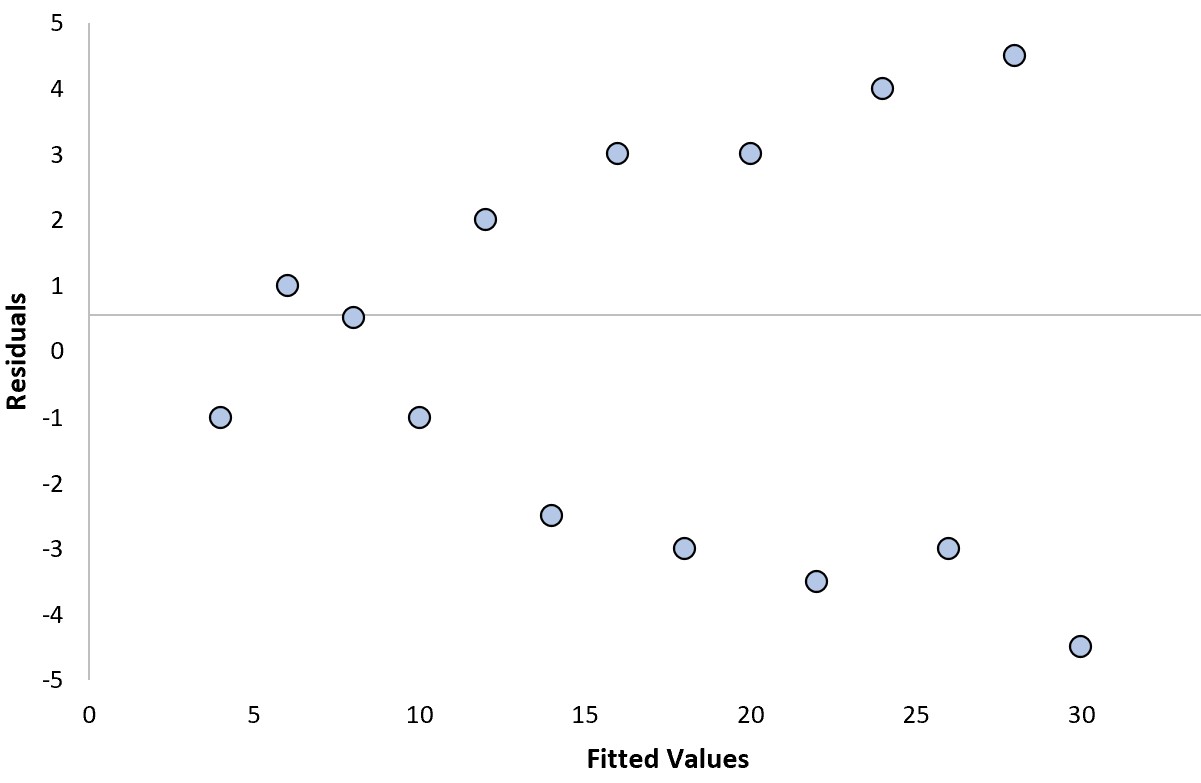
Possiamo rispondere alle seguenti due domande per determinare se si tratta di un diagramma residuo “buono”:

1. I residui mostrano un trend chiaro?

No. Non c’è una tendenza chiara nei residui.

2. I residui aumentano o diminuiscono sistematicamente nella varianza?

Sì . La varianza dei residui aumenta all’aumentare dei valori adattati.

Poiché abbiamo risposto “Sì” ad almeno una di queste domande, la considereremmo una trama residua “cattiva”.

In questo esempio particolare, i residui soffrono di eteroschedasticità , che si riferisce a una varianza disuguale dei residui a diversi livelli dei valori adattati.

Ciò significa che i risultati del modello di regressione potrebbero non essere affidabili.

Fare riferimento a questo articolo per apprendere diversi modi per risolvere il problema dell’eteroschedasticità in un modello di regressione.

Risorse addizionali

I seguenti tutorial spiegano come creare grafici dei residui utilizzando diversi software statistici:

Come creare una trama residua in R
Come creare un grafico residuo in Python
Come creare un grafico residuo in Excel
Come creare un grafico residuo in SAS