Come tracciare i risultati di regressione lineare multipla in r

Quando eseguiamo una regressione lineare semplice in R, è facile visualizzare la linea di regressione adattata perché stiamo lavorando solo con una singola variabile predittrice e una singola variabile di risposta .

Ad esempio, il codice seguente mostra come adattare un modello di regressione lineare semplice a un set di dati e tracciare i risultati:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

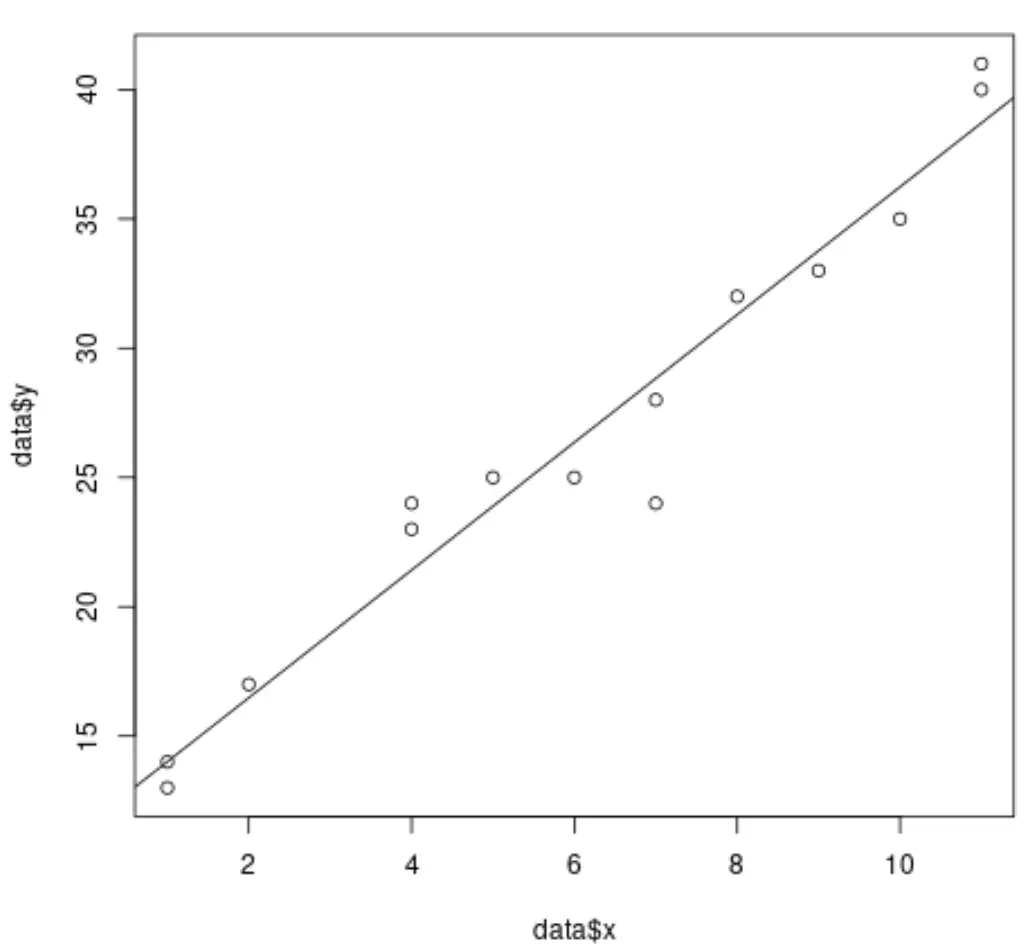
Tuttavia, quando eseguiamo una regressione lineare multipla, diventa difficile visualizzare i risultati perché esistono più variabili predittive e non possiamo semplicemente tracciare una linea di regressione su un grafico 2D.

Possiamo invece utilizzare grafici con variabili aggiunte (a volte chiamati “grafici di regressione parziale”), che sono grafici individuali che mostrano la relazione tra la variabile di risposta e una variabile predittrice, controllando al contempo la presenza di altre variabili predittive nel modello .

L’esempio seguente mostra come eseguire una regressione lineare multipla in R e visualizzare i risultati utilizzando grafici con variabili aggiunte.

Esempio: tracciare i risultati della regressione lineare multipla in R

Supponiamo di adattare il seguente modello di regressione lineare multipla a un set di dati in R utilizzando il set di dati mtcars integrato:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Dai risultati, possiamo vedere che il valore p per ciascuno dei coefficienti è inferiore a 0,1. Per semplicità, assumeremo che ciascuna delle variabili predittive sia significativa e debba essere inclusa nel modello.

Per produrre grafici delle variabili aggiunte, possiamo utilizzare la funzione avPlots() dal pacchetto car :

 #load car package
library(car)

#produce added variable plots
avPlots(model)

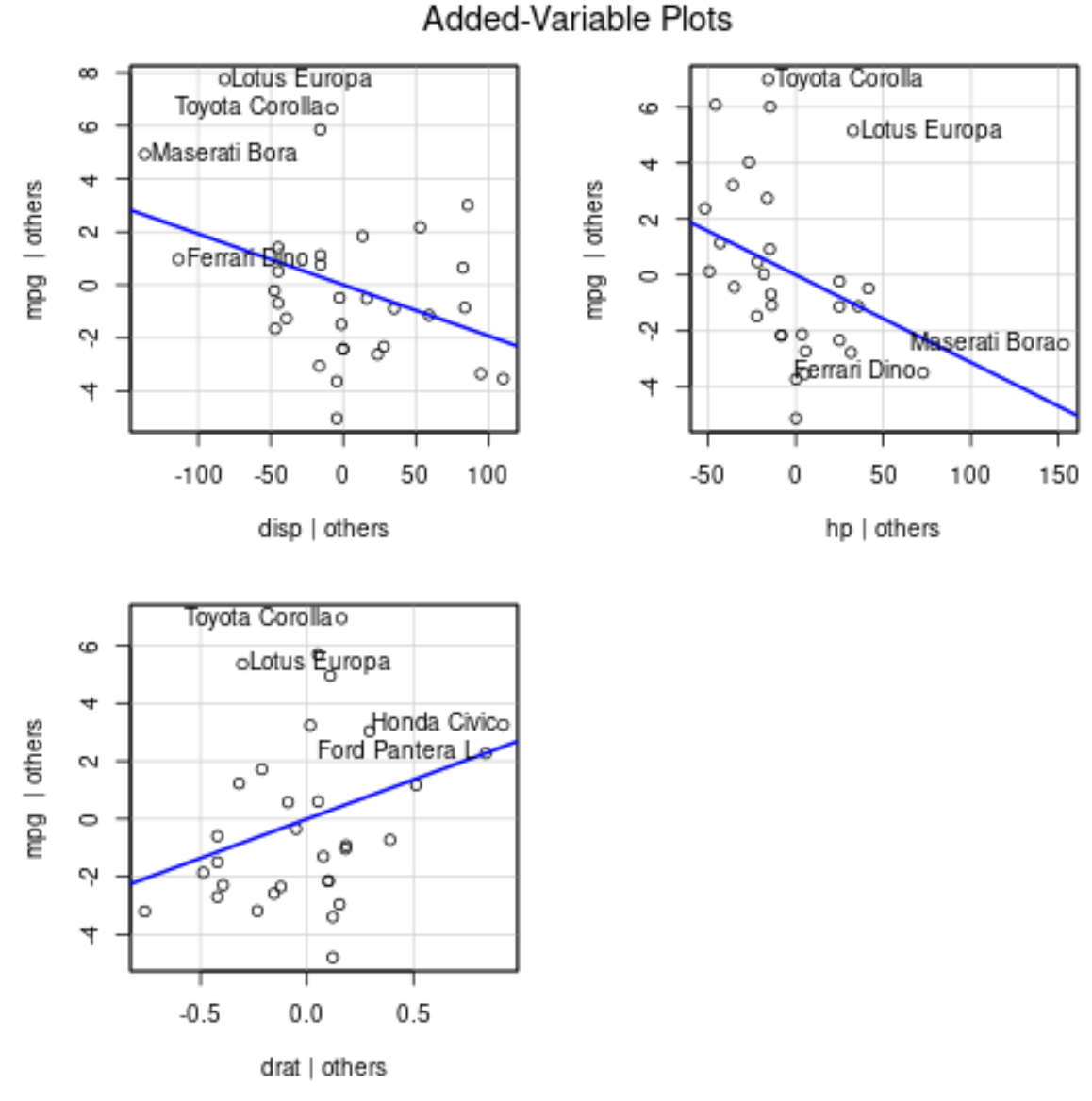
Ecco come interpretare ciascuna trama:

• L’asse x mostra una singola variabile predittrice e l’asse y mostra la variabile di risposta.
• La linea blu mostra l’associazione tra la variabile predittore e la variabile di risposta, mantenendo costante il valore di tutte le altre variabili predittive .
• I punti etichettati in ciascun grafico rappresentano le 2 osservazioni con i residui maggiori e le 2 osservazioni con la leva parziale maggiore.

Si noti che l’angolo della linea in ciascun grafico corrisponde al segno del coefficiente dell’equazione di regressione stimata.

Ad esempio, ecco i coefficienti stimati per ciascuna variabile predittrice nel modello:

• visualizzazione: -0,019232
• cap: -0,031229
• data: 2.714975

Si noti che l’angolo della linea è positivo nel grafico della variabile aggiunta per drat mentre è negativo per disp e hp , che corrisponde ai segni dei loro coefficienti stimati:

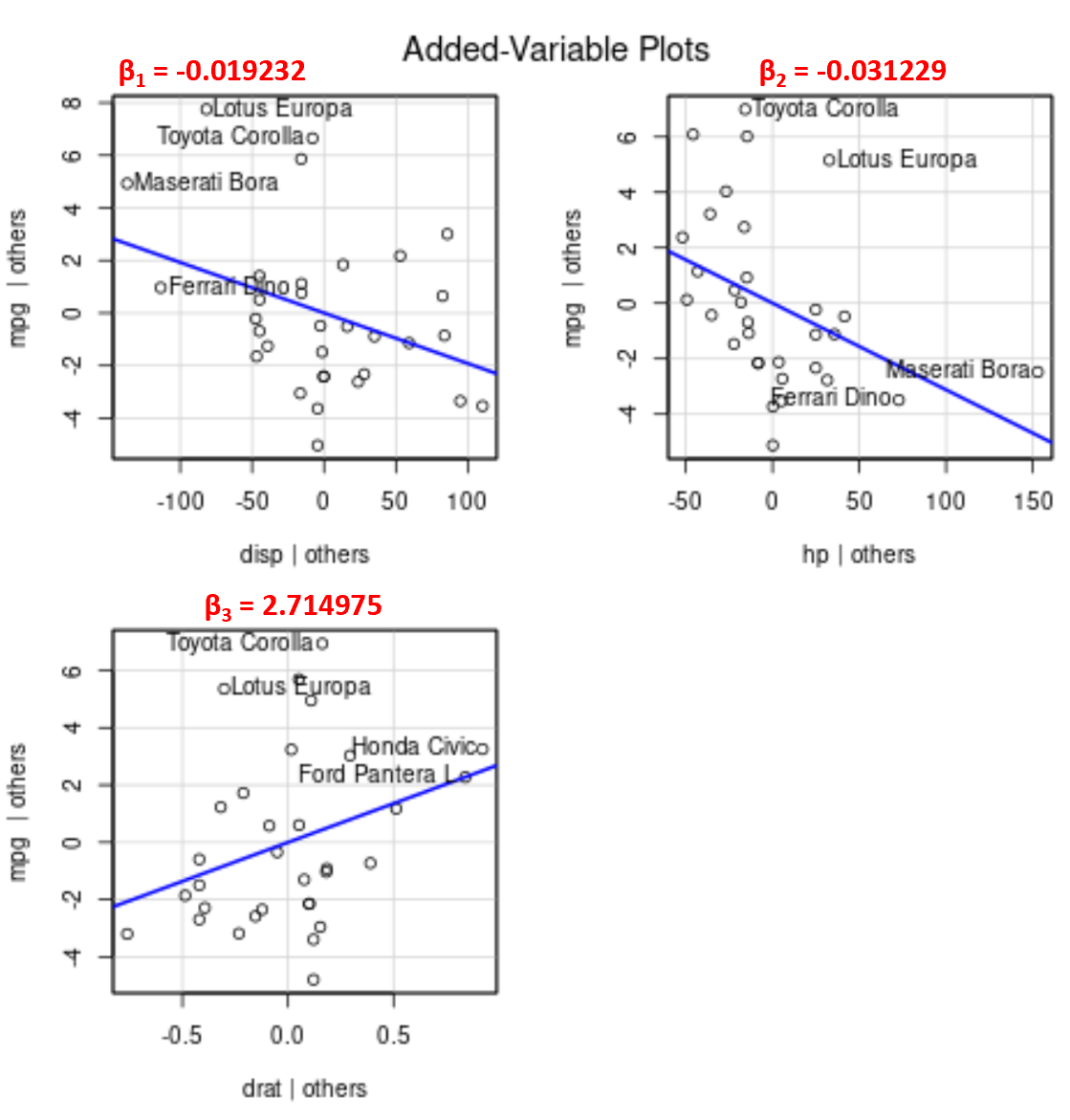
Sebbene non sia possibile tracciare una singola linea di regressione adattata su un grafico 2D poiché disponiamo di più variabili predittive, questi grafici con variabili aggiunte ci consentono di osservare la relazione tra ogni singola variabile predittiva e la variabile di risposta mantenendo costanti le altre variabili predittive.