Come trasformare i dati in python (log, radice quadrata, radice cubica)

Molti test statistici presuppongono che i set di dati siano distribuiti normalmente. Tuttavia, nella pratica spesso ciò non avviene.

Un modo per risolvere questo problema è trasformare la distribuzione dei valori in un set di dati utilizzando una delle tre trasformazioni:

1. Trasformazione del log: trasforma la variabile di risposta da y a log(y) .

2. Trasformazione della radice quadrata: trasforma la variabile di risposta da y a √y .

3. Trasformazione della radice del cubo: trasforma la variabile di risposta da y a y ^1/3 .

Eseguendo queste trasformazioni, il set di dati generalmente diventa distribuito in modo più normale.

Gli esempi seguenti mostrano come eseguire queste trasformazioni in Python.

Trasformazione del registro in Python

Il codice seguente mostra come eseguire una trasformazione logaritmica su una variabile e creare grafici affiancati per visualizzare la distribuzione originale e la distribuzione dei dati trasformata in logaritmo:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 4 , b= 15 , size= 300 )

#create log-transformed data
data_log = np. log (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Log-Transformed Data ')

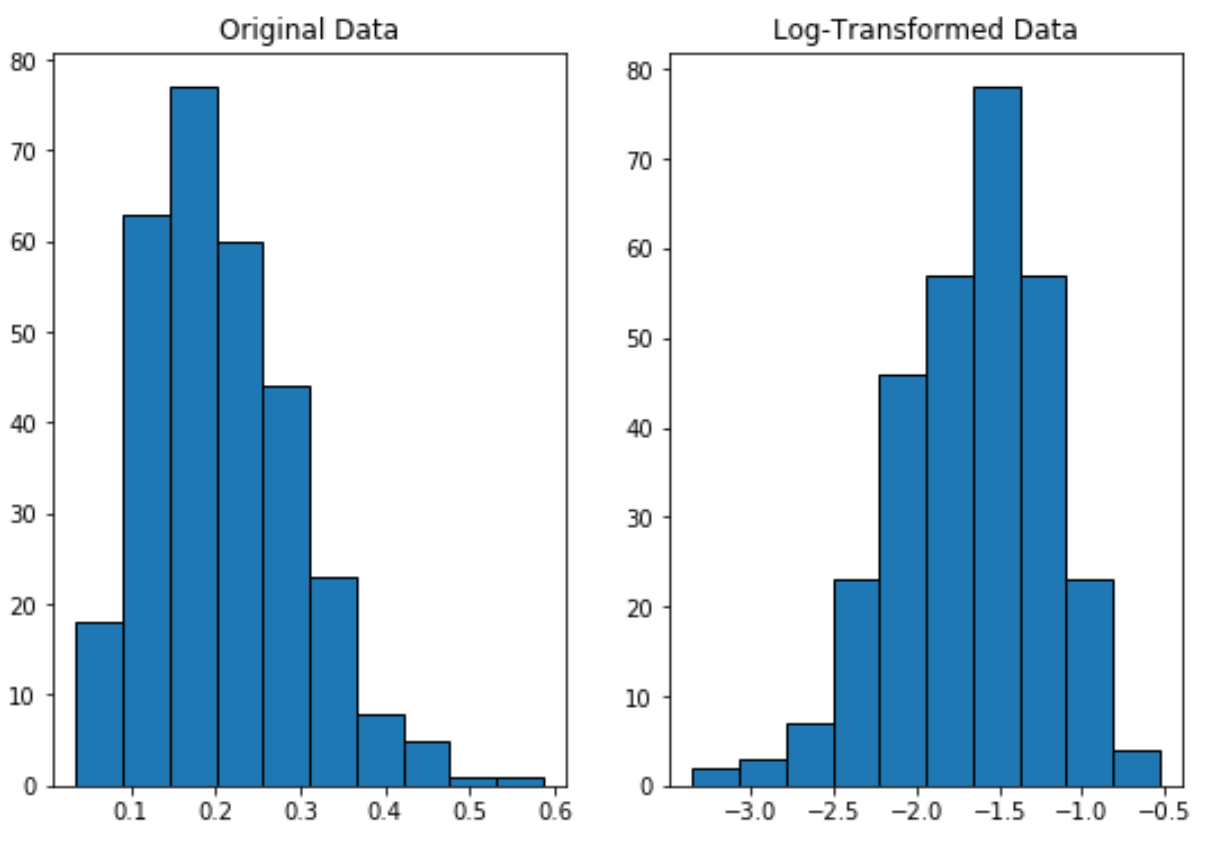
Notare come la distribuzione trasformata in log sia distribuita in modo più normale rispetto alla distribuzione originale.

Non ha ancora una perfetta “forma a campana”, ma è più vicina a una distribuzione normale che a quella originale.

Trasformazione della radice quadrata in Python

Il codice seguente mostra come eseguire una trasformazione radice quadrata su una variabile e creare grafici affiancati per visualizzare la distribuzione originale e la distribuzione trasformata radice quadrata dei dati:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. sqrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Square Root Transformed Data ') 

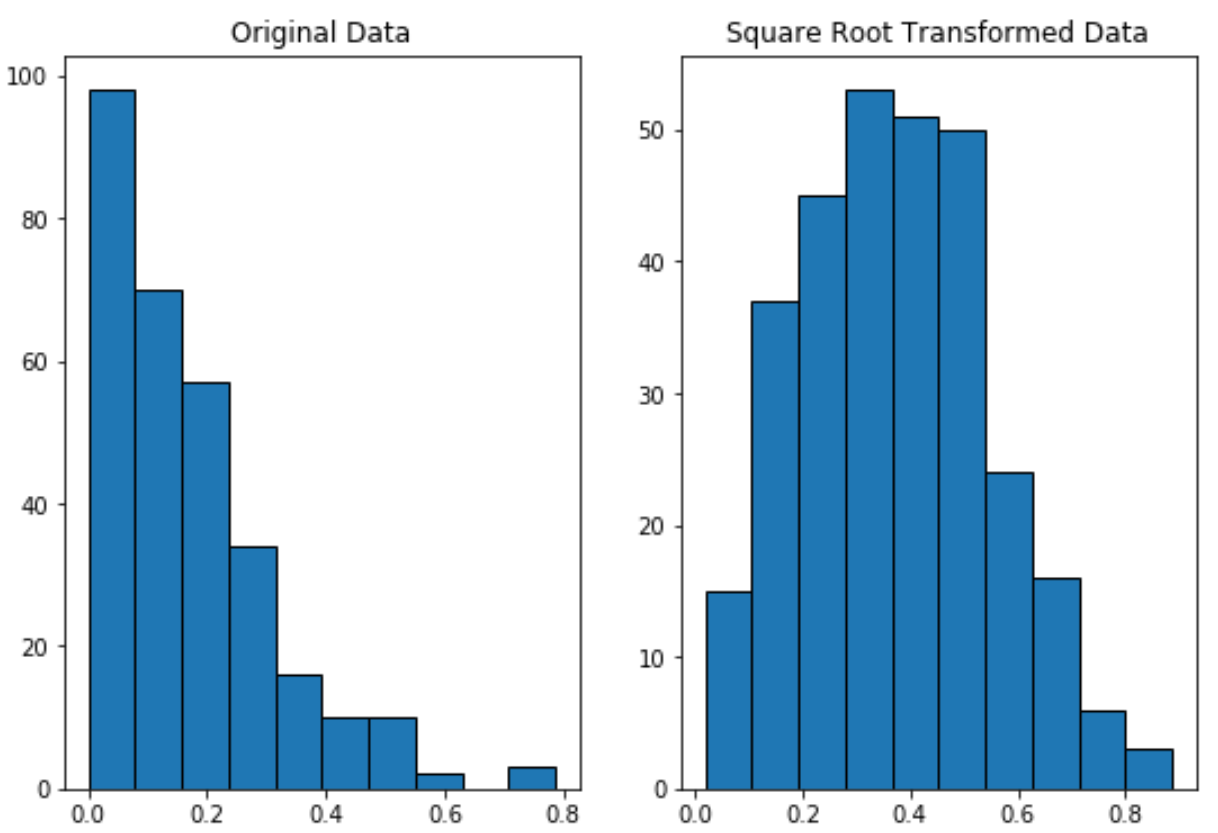
Si noti come i dati trasformati con radice quadrata siano distribuiti in modo molto più normale rispetto ai dati originali.

Trasformazione della radice del cubo in Python

Il codice seguente mostra come eseguire una trasformazione di radice cubica su una variabile e creare grafici affiancati per visualizzare la distribuzione originale e la distribuzione trasformata di radice cubica dei dati:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. cbrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Cube Root Transformed Data ') 

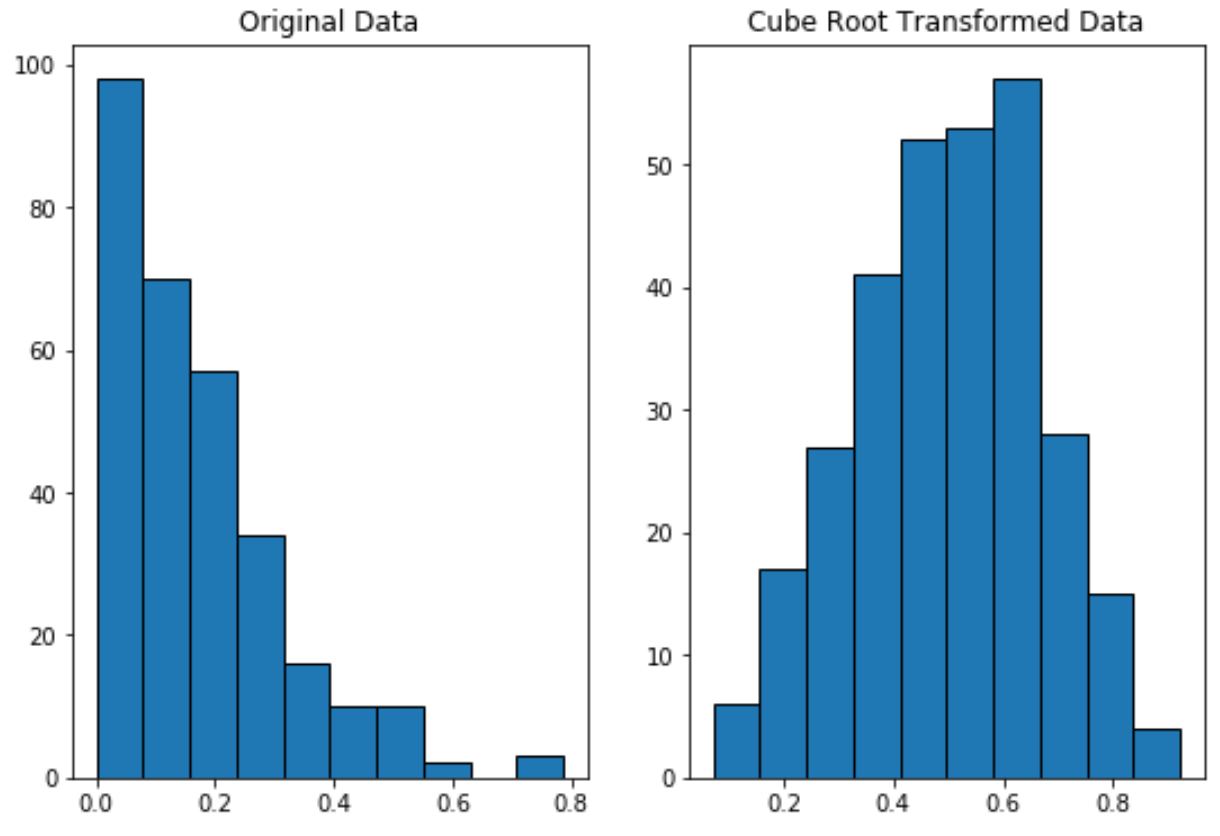
Si noti come i dati trasformati della radice cubica siano distribuiti in modo molto più normale rispetto ai dati originali.

Risorse addizionali

Come calcolare i punteggi Z in Python
Come normalizzare i dati in Python
Qual è il presupposto di normalità in statistica?