Come trasformare i dati in r (log, radice quadrata, radice cubica)

Molti test statistici presuppongono che i residui di una variabile di risposta siano distribuiti normalmente.

Tuttavia, i residui spesso non sono distribuiti normalmente. Un modo per risolvere questo problema è trasformare la variabile di risposta utilizzando una delle tre trasformazioni:

1. Trasformazione del log: trasforma la variabile di risposta da y a log(y) .

2. Trasformazione della radice quadrata: trasforma la variabile di risposta da y a √y .

3. Trasformazione della radice del cubo: trasforma la variabile di risposta da y a y ^1/3 .

Eseguendo queste trasformazioni, la variabile di risposta generalmente si avvicina alla distribuzione normale. Gli esempi seguenti mostrano come eseguire queste trasformazioni in R.

Trasformazione logaritmica in R

Il codice seguente mostra come eseguire una trasformazione del log su una variabile di risposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Il codice seguente mostra come creare istogrammi per visualizzare la distribuzione di y prima e dopo l’esecuzione di una trasformazione del registro:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

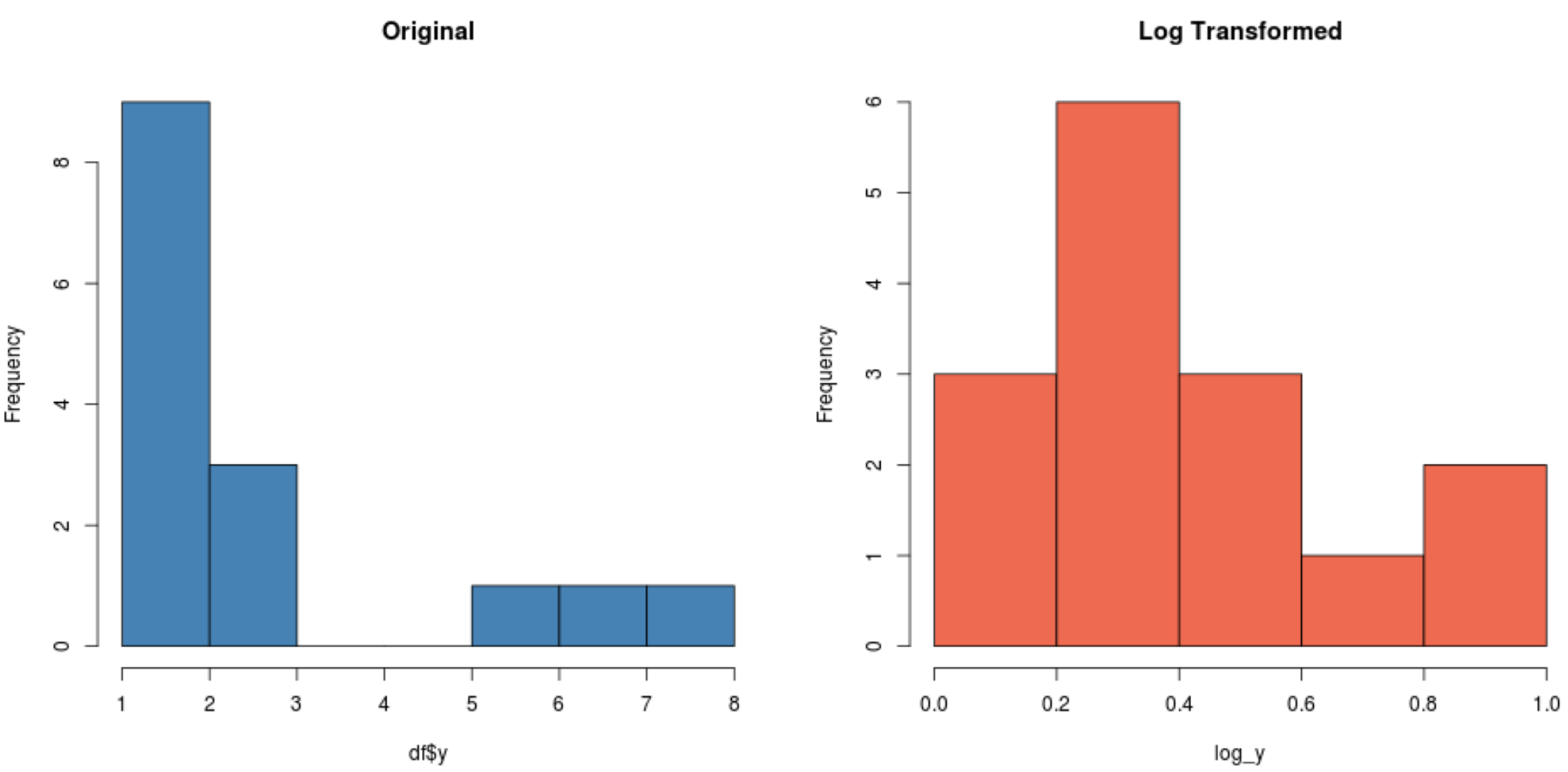
Nota come la distribuzione trasformata in log sia molto più normale della distribuzione originale. Non ha ancora una perfetta “forma a campana”, ma è più vicina a una distribuzione normale che a quella originale.

Infatti, se eseguiamo un test di Shapiro-Wilk su ciascuna distribuzione, troveremo che la distribuzione originale fallisce l’ipotesi di normalità, mentre la distribuzione trasformata logaritmica no (a α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Trasformazione della radice quadrata in R

Il codice seguente mostra come eseguire una trasformazione radice quadrata su una variabile di risposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Il codice seguente mostra come creare istogrammi per visualizzare la distribuzione di y prima e dopo l’esecuzione di una trasformazione della radice quadrata:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

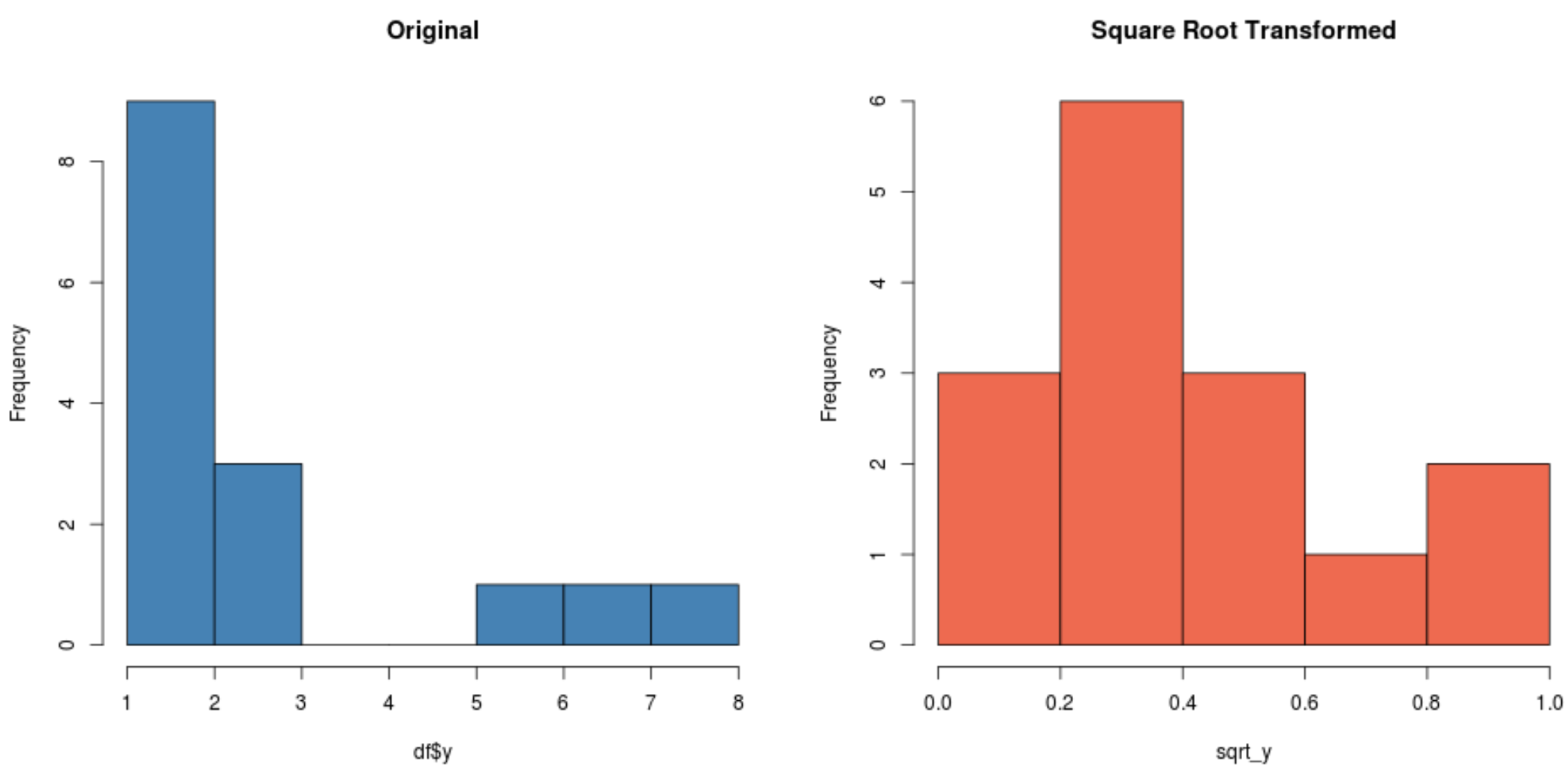
Si noti come la distribuzione trasformata radice quadrata sia distribuita in modo molto più normale rispetto alla distribuzione originale.

Trasformazione della radice cubica in R

Il codice seguente mostra come eseguire una trasformazione della radice cubica su una variabile di risposta:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Il codice seguente mostra come creare istogrammi per visualizzare la distribuzione di y prima e dopo l’esecuzione di una trasformazione della radice quadrata:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

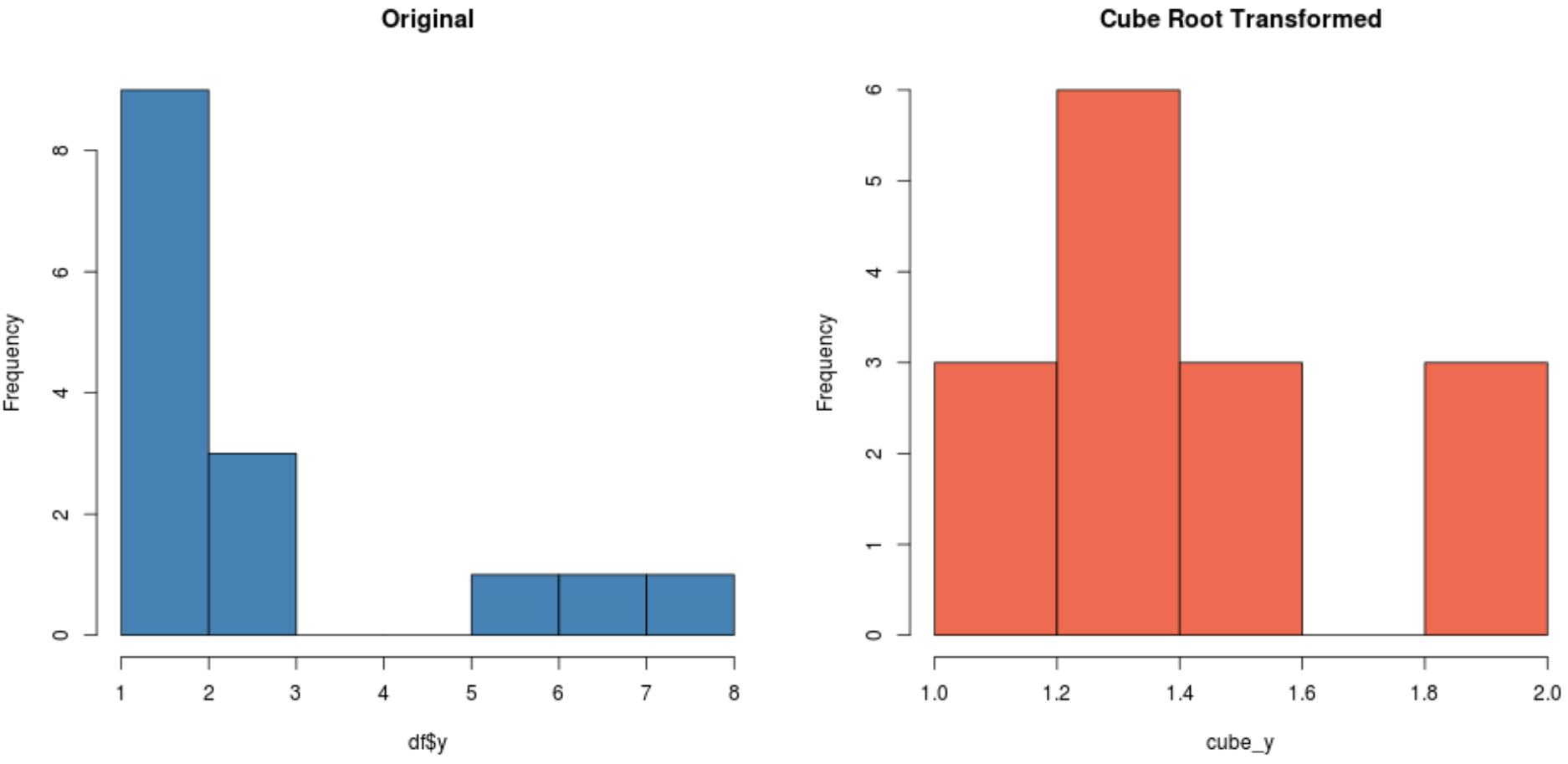
A seconda del set di dati, una di queste trasformazioni potrebbe produrre un nuovo set di dati distribuito in modo più normale rispetto agli altri.