Come eseguire una trasformazione box-cox in r (con esempi)

Una trasformazione box-cox è un metodo comunemente utilizzato per trasformare un set di dati non distribuito normalmente in un set distribuito più normalmente .

L’idea alla base di questo metodo è trovare un valore per λ tale che i dati trasformati siano il più vicino possibile alla distribuzione normale, utilizzando la seguente formula:

• y(λ) = (y ^λ – 1) / λ se y ≠ 0
• y(λ) = log(y) se y = 0

Possiamo eseguire una trasformazione box-cox in R utilizzando la funzione boxcox() dalla libreria MASS() . L’esempio seguente mostra come utilizzare questa funzione nella pratica.

Fare riferimento a questo articolo dell’Università del Connecticut per un bel riassunto dello sviluppo della trasformazione Box-Cox.

Esempio: trasformazione di Box-Cox in R

Il codice seguente mostra come adattare un modello di regressione lineare a un set di dati, quindi utilizzare la funzione boxcox() per trovare un lambda ottimale per trasformare la variabile di risposta e adattare un nuovo modello.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

Il lambda ottimale si è rivelato essere -0.4242424 . Pertanto, il nuovo modello di regressione ha sostituito la variabile di risposta originale y con la variabile y = (y ^-0,4242424 – 1) / -0,4242424.

Il codice seguente mostra come creare due grafici QQ in R per visualizzare le differenze nei residui tra i due modelli di regressione:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

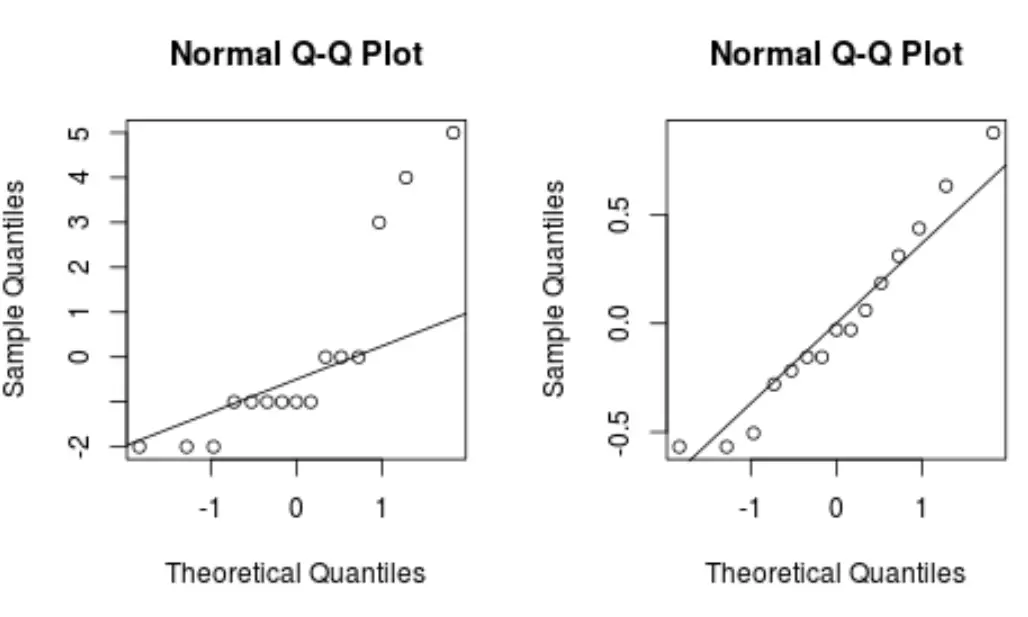
Generalmente, se i punti dati si trovano lungo una linea diagonale retta in un grafico QQ, il set di dati probabilmente segue una distribuzione normale.

Si noti come il modello trasformato di box-cox produce un grafico QQ con una linea molto più retta rispetto al modello di regressione originale.

Ciò indica che i residui del modello trasformato di box-cox sono distribuiti molto più normalmente, il che soddisfa uno dei presupposti della regressione lineare .

Risorse addizionali

Come trasformare i dati in R (log, radice quadrata, radice cubica)
Come creare e interpretare un grafico QQ in R
Come eseguire un test di Shapiro-Wilk per la normalità in R