Come trovare una probabilità data una media e una deviazione standard

Possiamo utilizzare il seguente processo per trovare la probabilità che una variabile casuale distribuita normalmente

Passaggio 1: trova il punteggio z.

Un punteggio z indica di quante deviazioni standard un singolo valore di dati cade dalla media. Viene calcolato come segue:

Punteggio z = (x – μ) / σ

Oro:

• x: valore del dato individuale
• μ: media della popolazione
• σ: deviazione standard della popolazione

Passaggio 2: trova la probabilità che corrisponde al punteggio z.

Una volta calcolato il punteggio z, possiamo trovare la probabilità corrispondente nella tabella z.

Gli esempi seguenti mostrano come utilizzare questo processo in diversi scenari.

Esempio 1: Probabilità inferiore a un certo valore

I punteggi di un determinato test sono normalmente distribuiti con media μ = 82 e deviazione standard σ = 8. Qual è la probabilità che un dato studente ottenga meno di 84 nel test?

Passaggio 1: trova il punteggio z.

Per prima cosa troveremo lo z-score associato ad un punteggio pari a 84:

Punteggio z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Passaggio 2: utilizzare la tabella z per trovare la probabilità corrispondente.

Successivamente, cercheremo il valore 0,25 nella tabella z:

La probabilità che un dato studente ottenga un punteggio inferiore a 84 è di circa il 59,87% .

Esempio 2: Probabilità maggiore di un certo valore

L’altezza di una certa specie di pinguino è normalmente distribuita con una media di μ = 30 pollici e una deviazione standard di σ = 4 pollici. Se selezioniamo un pinguino a caso, qual è la probabilità che sia alto più di 28 pollici?

Passaggio 1: trova il punteggio z.

Per prima cosa troveremo il punteggio z associato ad un’altezza di 28 pollici.

Punteggio z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Passaggio 2: utilizzare la tabella z per trovare la probabilità corrispondente.

Successivamente cercheremo il valore -0,5   nella tabella z:

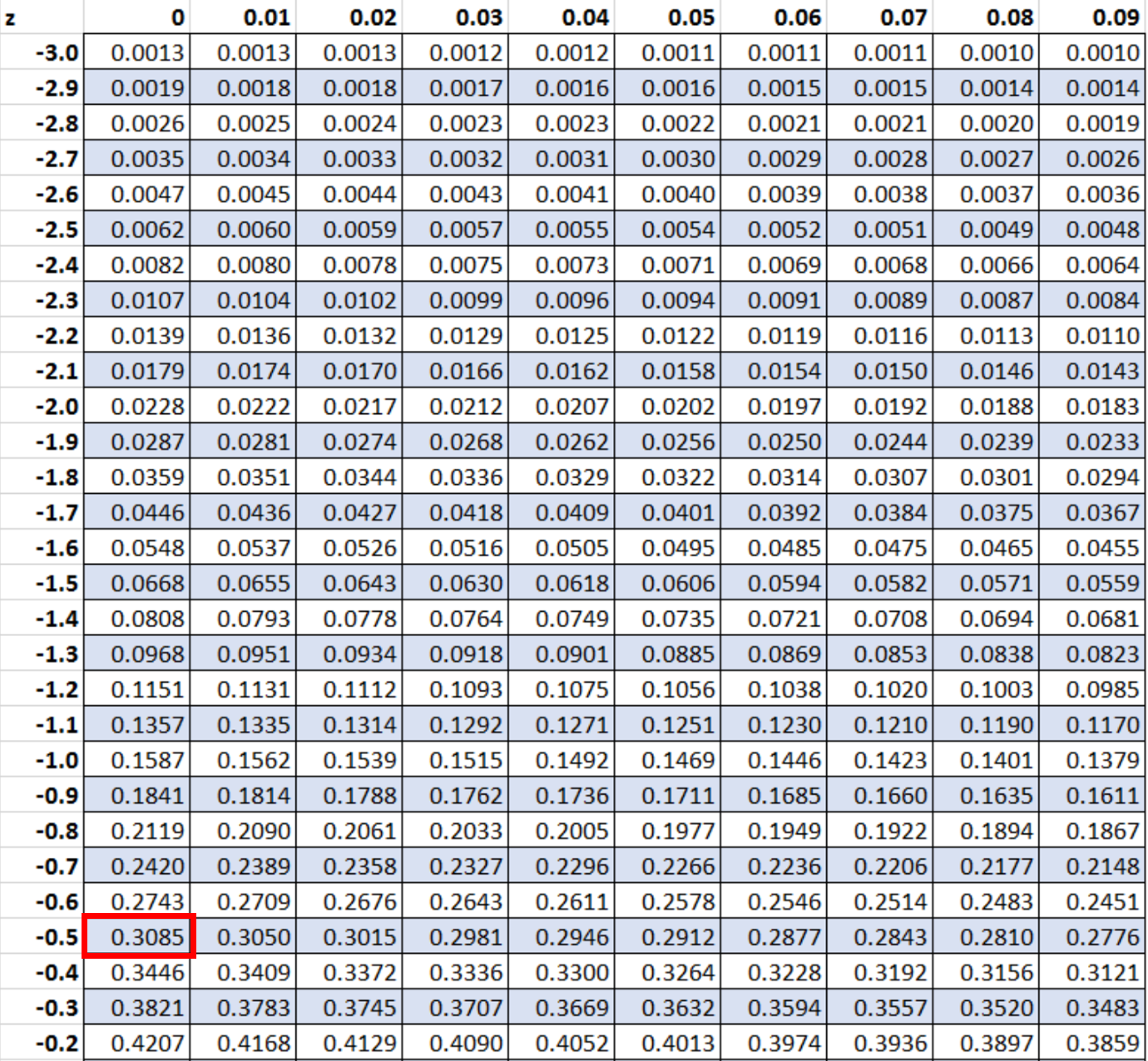
Il valore che corrisponde a un punteggio z di -0,5 è 0,3085. Ciò rappresenta la probabilità che un pinguino sia più basso di 28 pollici.

Tuttavia, poiché vogliamo conoscere la probabilità che un pinguino sia più alto di 28 pollici, dobbiamo sottrarre tale probabilità da 1.

Quindi, la probabilità che un pinguino sia più alto di 28 pollici è: 1 – 0,3085 = 0,6915 .

Esempio 3: Probabilità tra due valori

Il peso di una certa specie di tartaruga è normalmente distribuito con una media di μ = 400 libbre e una deviazione standard di σ = 25 libbre. Se selezioniamo una tartaruga a caso, qual è la probabilità che pesi tra 410 e 425 libbre?

Passaggio 1: trova i punteggi z.

Per prima cosa troveremo i punteggi z associati a 410 libri e 425 libri

Punteggio z di 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

punteggio z di 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Passaggio 2: utilizzare la tabella z per trovare la probabilità corrispondente.

Per prima cosa cercheremo il valore 0.4   nella tabella z:

Successivamente cercheremo il valore 1   nella tabella z:

Successivamente, sottraiamo il valore più piccolo dal valore più grande: 0,8413 – 0,6554 = 0,1859 .

Quindi la probabilità che una tartaruga selezionata casualmente pesi tra 410 e 425 libbre è del 18,59% .

Risorse addizionali

Come calcolare manualmente un valore P da un punteggio Z
Come convertire i punteggi Z in punteggi grezzi
Come trovare i punteggi Z in una determinata area