Come trovare valori anomali utilizzando l'intervallo interquartile

Un valore anomalo è un’osservazione anormalmente distante da altri valori in un set di dati. I valori anomali possono essere problematici perché possono influenzare i risultati di un’analisi.

Un modo comune per rilevare valori anomali in un set di dati è utilizzare l’ intervallo interquartile .

L’intervallo interquartile, spesso abbreviato IQR, è la differenza tra il 25° percentile (Q1) e il 75° percentile (Q3) in un set di dati. Misura la distribuzione media del 50% dei valori.

Un metodo popolare consiste nel dichiarare un’osservazione come un valore anomalo se ha un valore 1,5 volte superiore all’IQR o 1,5 volte inferiore all’IQR.

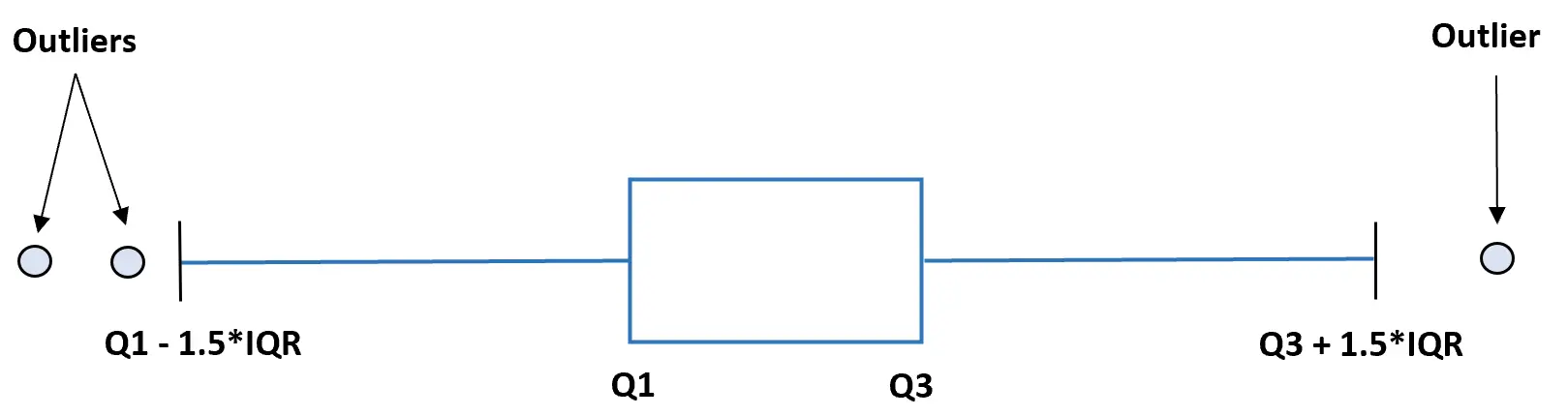
Questo tutorial fornisce un esempio passo passo di come trovare valori anomali in un set di dati utilizzando questo metodo.

Passaggio 1: creare i dati

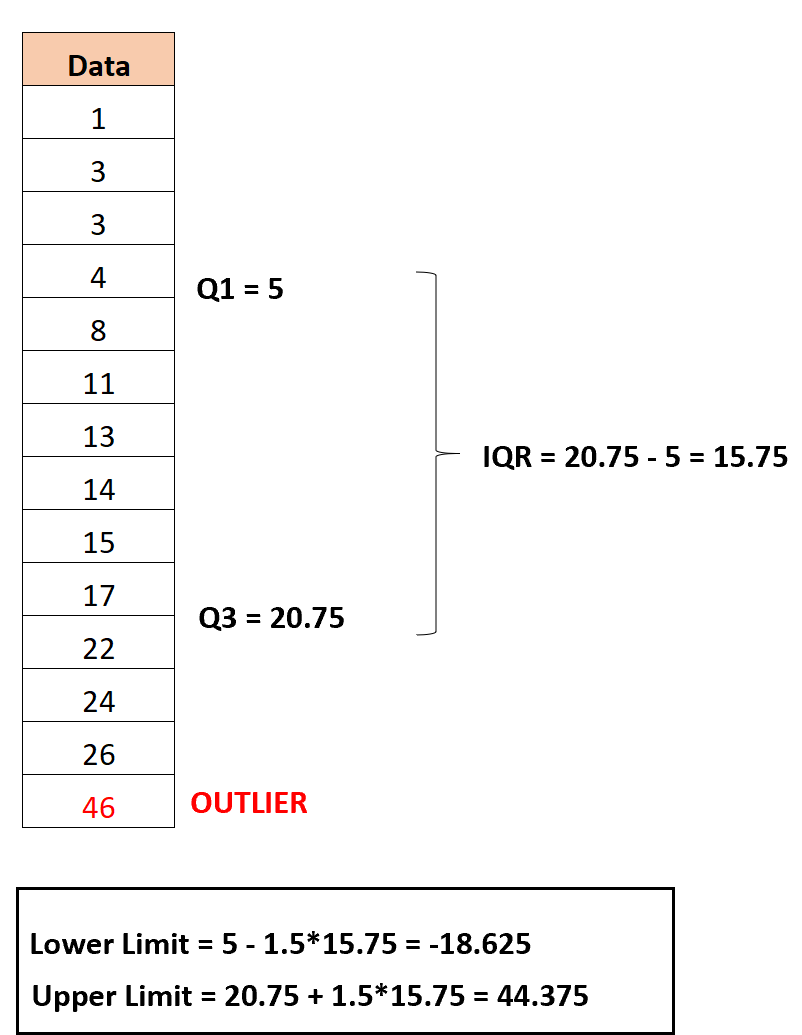
Supponiamo di avere il seguente set di dati:

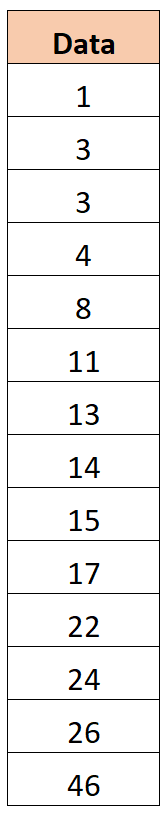
Passaggio 2: identificare il primo e il terzo quartile

Il primo quartile risulta essere 5 e il terzo quartile risulta essere 20,75 .

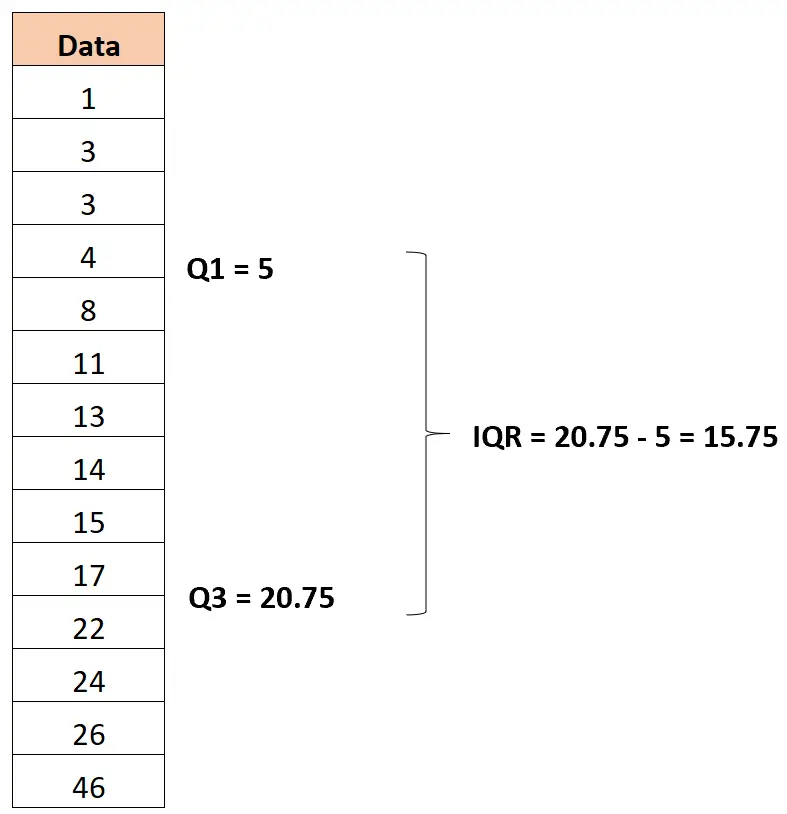
Pertanto, l’intervallo interquartile risulta essere 20,75 -5 = 15,75 .

Passaggio 3: trova i limiti inferiore e superiore

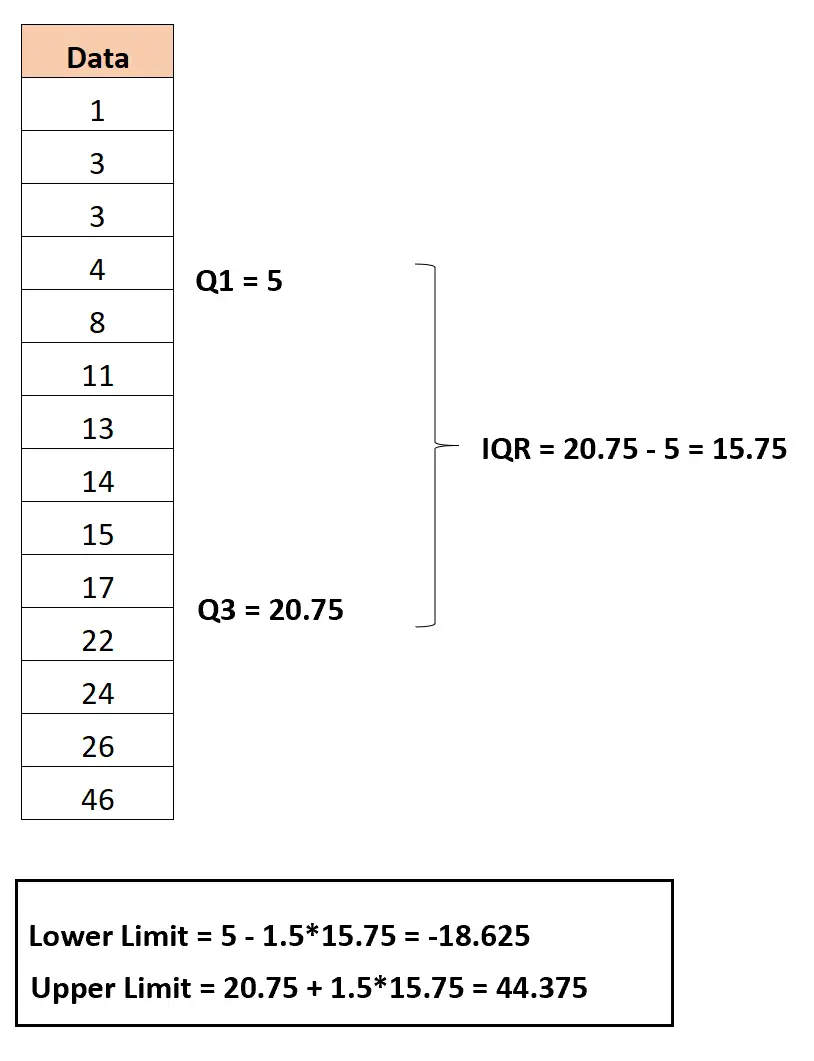
Il limite inferiore è calcolato come segue:

Limite inferiore = Q1 – 1,5*IQR = 5 – 1,5*15,75 = -18,625

E il limite superiore è calcolato come segue:

Limite superiore = Q3 + 1,5*IQR = 20,75 + 1,5*15,75 = 44,375

Passaggio 4: identificare i valori anomali

L’unica osservazione nel set di dati con un valore inferiore al limite inferiore o superiore al limite superiore è 46 . Quindi questo è l’unico valore anomalo in questo set di dati.

Nota: è possibile utilizzare questo calcolatore dei limiti anomali per trovare automaticamente i limiti superiore e inferiore degli outlier in un determinato set di dati.

Come trovare valori anomali nella pratica

I seguenti tutorial spiegano come trovare valori anomali utilizzando l’intervallo interquartile in diversi software statistici:

Come trovare valori anomali in Excel
Come trovare valori anomali in R
Come trovare valori anomali in Python
Come trovare valori anomali in SPSS