Come eseguire un test t per un campione in spss

Un test t su un campione viene utilizzato per verificare se la media di una popolazione è uguale o meno a un determinato valore.

Questo tutorial spiega come eseguire un test t per un campione in SPSS.

Esempio: test t per un campione in SPSS

Un botanico vuole sapere se l’altezza media di una certa specie di piante è pari a 15 pollici. Prende un campione casuale di 12 piante e registra ciascuna delle loro altezze in pollici:

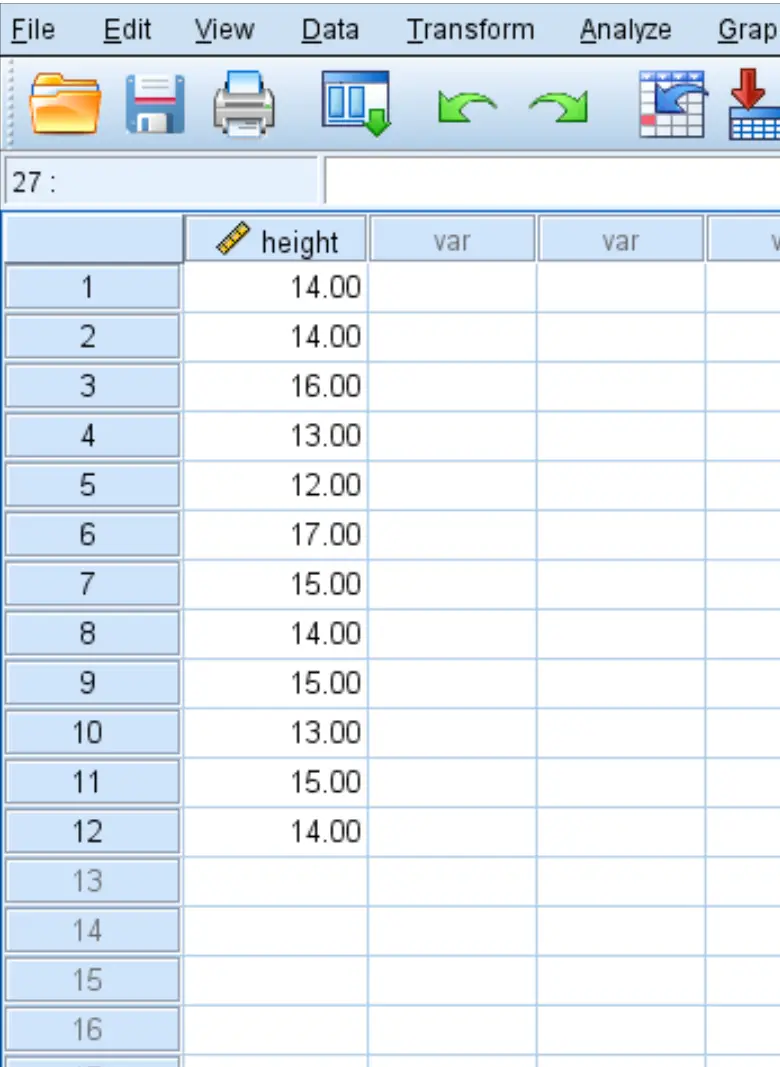
Utilizzare i seguenti passaggi per eseguire un test t su un campione per determinare se l’altezza media reale di questa specie di pianta è pari a 15 pollici, sulla base delle seguenti ipotesi nulle e alternative:

• H ₀ : μ = 15 (la media reale della popolazione è pari a 15 pollici)
• H ₁ : μ ≠ 15 (la vera media della popolazione non è uguale a 15 pollici)

Utilizzare un livello di significatività pari a α = 0,05.

Passaggio 1: scegliere l’opzione t-test per un campione.

Fare clic sulla scheda Analizza , quindi su Confronta medie , quindi su Test T per un campione :

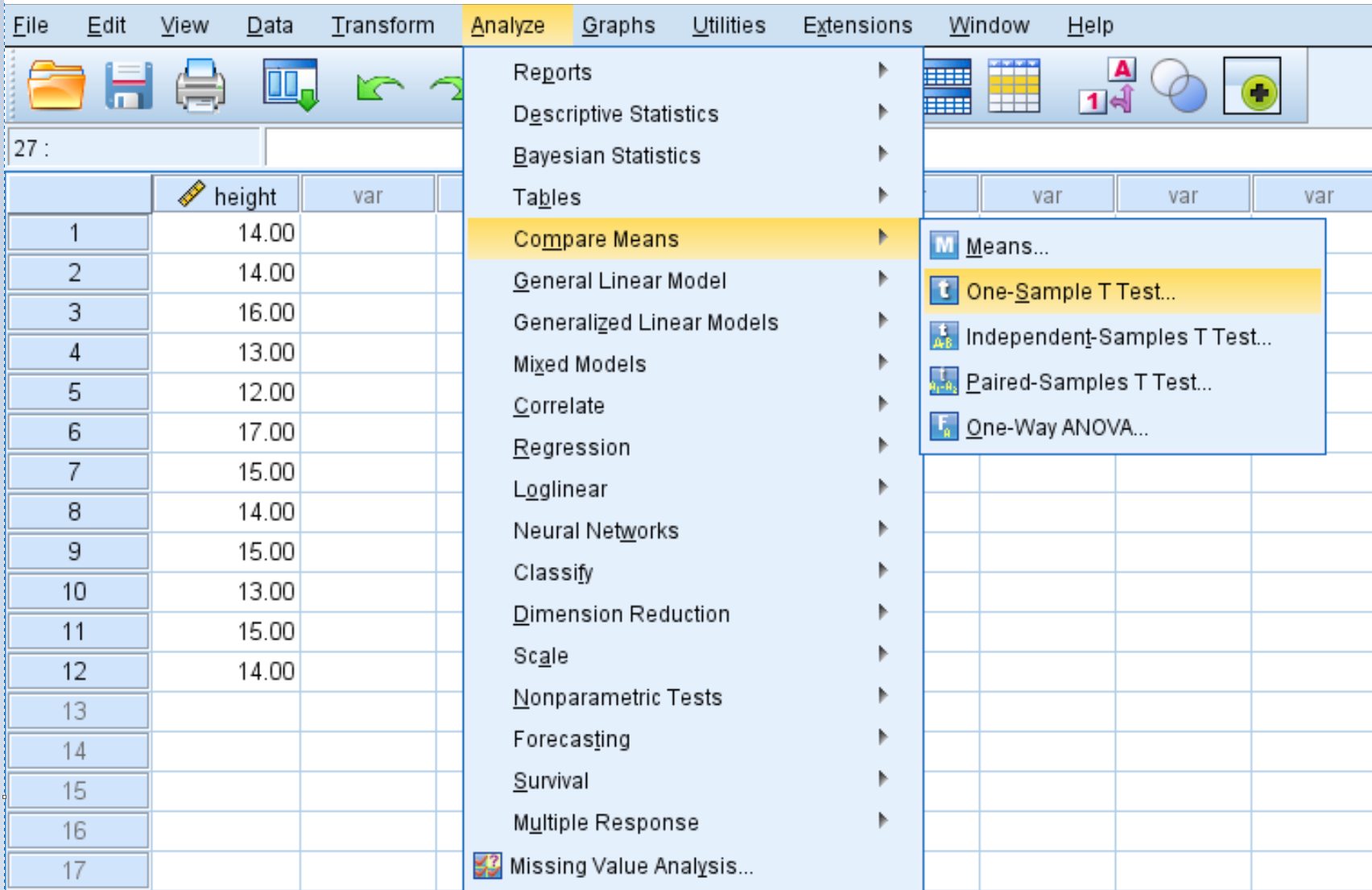
Passaggio 2: inserire i valori necessari per eseguire il t-test per un campione.

Dopo aver fatto clic su One-Sample T Test , verrà visualizzata la seguente finestra:

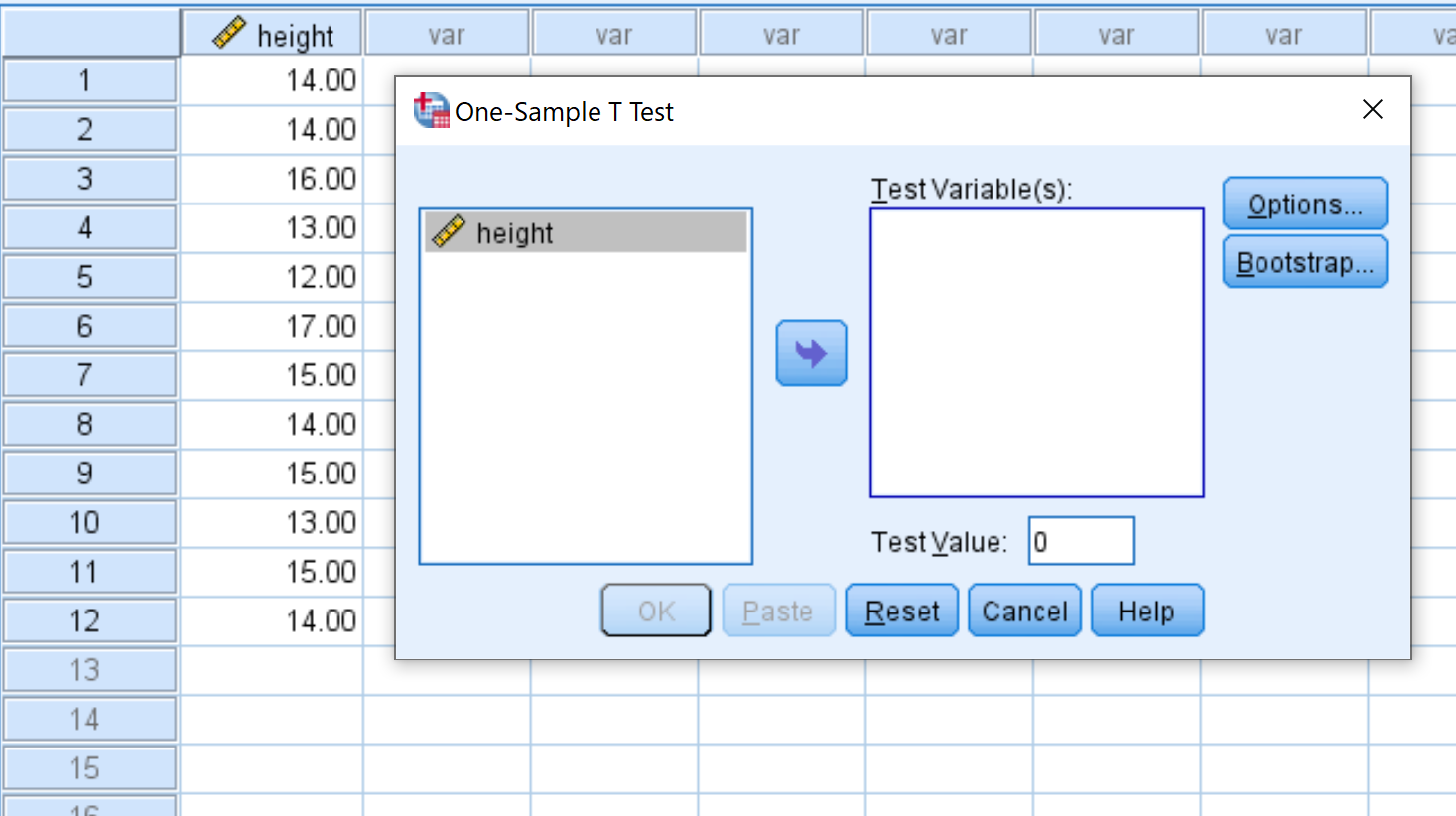
Trascina l’ altezza della variabile nella casella denominata Variabili di test e modifica il valore di test su 15. Quindi fai clic su OK .

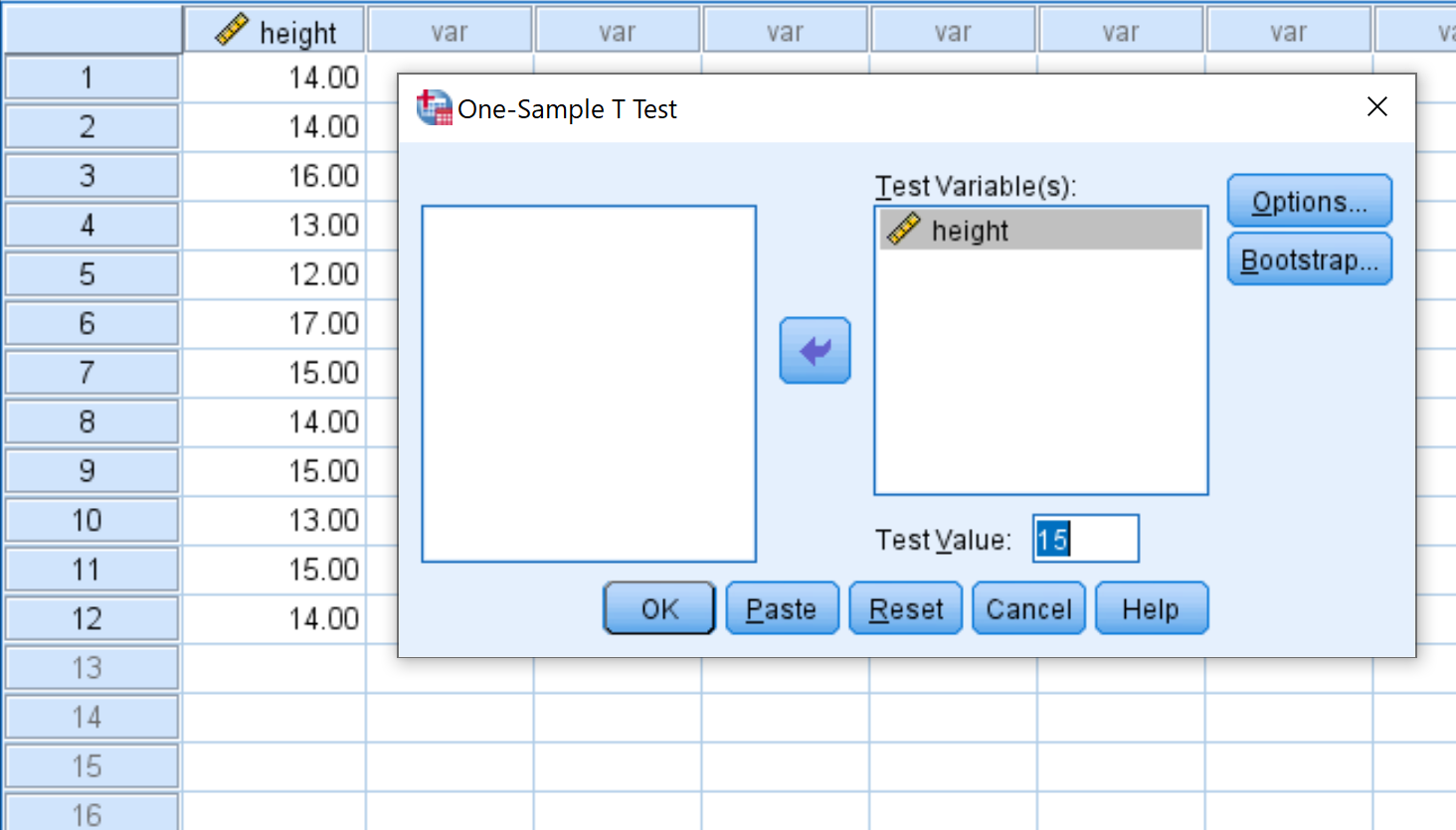
Passaggio 3: interpretare i risultati.

Dopo aver fatto clic su OK , verranno visualizzati i risultati del t-test per un campione:

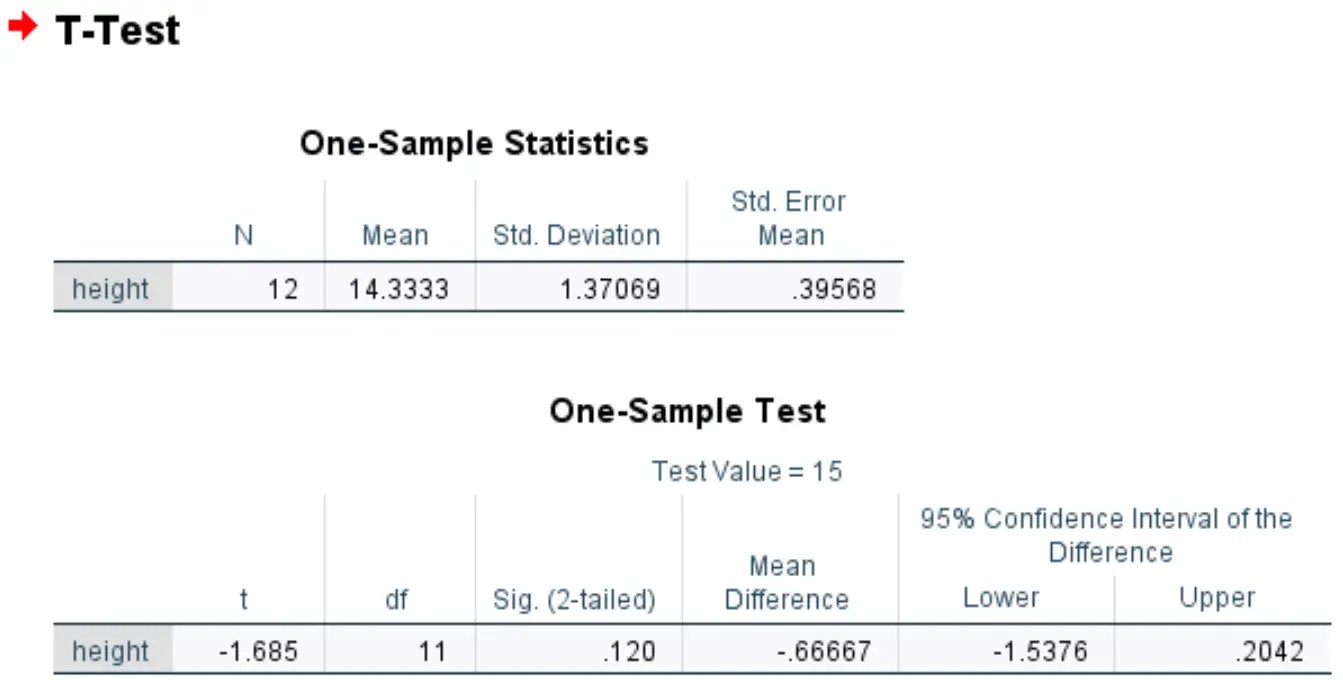
La prima tabella mostra le statistiche riassuntive per l’altezza variabile:

• N: dimensione del campione
• Media: altezza media delle piante del campione
• Standard. Deviazione: la deviazione standard dell’altezza della pianta nel campione.
• Standard. Errore medio: l’errore standard della media, calcolato come s/√n

La seconda tabella mostra i risultati del t-test per un campione:

• t: La statistica del test, calcolata come (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
• df: i gradi di libertà, calcolati come n-1 = 12-1 = 11
• Sig. (a due code): il valore p a due code che corrisponde a un valore di -1,685 con df=11
• Differenza media: la differenza tra la media campionaria e la media ipotetica
• IC al 95% della differenza: intervallo di confidenza al 95% per la differenza reale tra la media campionaria e la media ipotetica.

Poiché il valore p del test (0,120) non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che la vera altezza media di questa specie di pianta sia diversa da 15 pollici.