Uno z-score può essere negativo?

Nelle statistiche, un punteggio z ci dice quante deviazioni standard un valore è dalla media . Usiamo la seguente formula per calcolare uno z-score:

z = (X – μ) / σ

dove X è il valore che stiamo analizzando, μ è la media e σ è la deviazione standard.

Un punteggio z può essere positivo, negativo o zero.

Un punteggio z positivo indica che un valore particolare è superiore alla media, un punteggio z negativo indica che un valore particolare è inferiore alla media e un punteggio z pari a zero indica che un valore particolare è uguale alla media.

Alcuni esempi dovrebbero chiarirlo.

Esempi: calcolo di un punteggio Z

Supponiamo di avere il seguente set di dati che mostra l’altezza (in pollici) di un determinato gruppo di piante:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

La media campionaria di questo set di dati è 13 e la deviazione standard campionaria è 5,51 .

1. Trova il punteggio z per il valore “8” in questo set di dati.

Ecco come calcolare lo z-score:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Ciò significa che il valore “8” è 0,91 deviazioni standard inferiori alla media.

2. Trova il punteggio z per il valore “13” in questo set di dati.

Ecco come calcolare lo z-score:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Ciò significa che il valore “13” è esattamente uguale alla media.

3. Trova il punteggio z per il valore “20” in questo set di dati.

Ecco come calcolare lo z-score:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Ciò significa che il valore “20” è 1,28 deviazioni standard sopra la media.

Come interpretare i punteggi Z

Il grafico AZ ci dice quale percentuale di valori scende al di sotto di determinati punteggi Z. Alcuni esempi dovrebbero chiarirlo.

Esempio 1: punteggi Z negativi

In precedenza, abbiamo scoperto che il valore grezzo “8” nel nostro set di dati aveva un punteggio z di -0,91 . Secondo la tabella Z il 18,14% dei valori sono inferiori a questo valore.

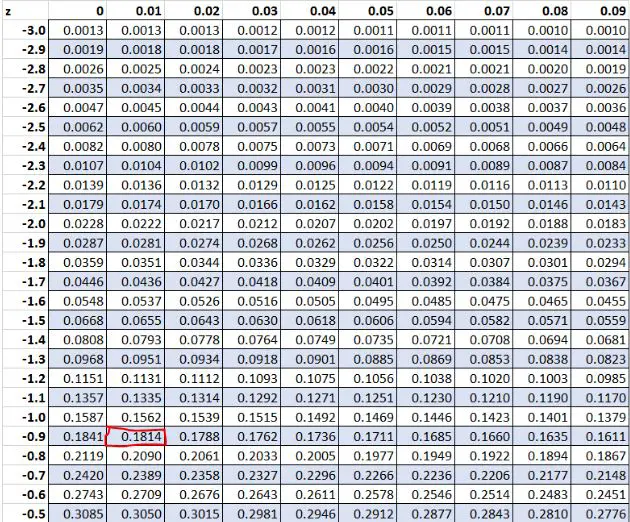
Esempio 2: Z-Score pari a zero

In precedenza, abbiamo scoperto che il valore grezzo “13” nel nostro set di dati aveva un punteggio z pari a 0 . Secondo la tabella Z il 50,00% dei valori sono inferiori a questo valore.

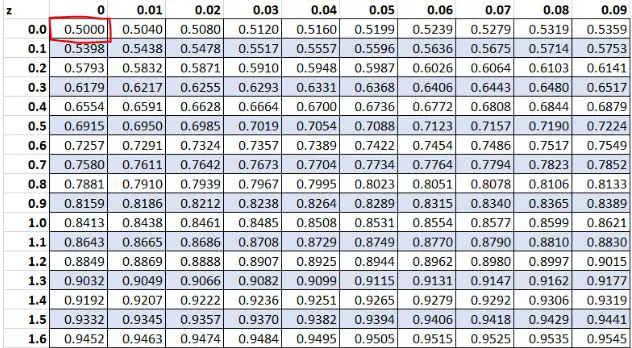
Esempio 3: punteggi Z positivi

In precedenza, abbiamo scoperto che il valore grezzo “20” nel nostro set di dati aveva un punteggio z di 1,28 . Secondo la tabella Z l’89,97% dei valori sono inferiori a questo valore.

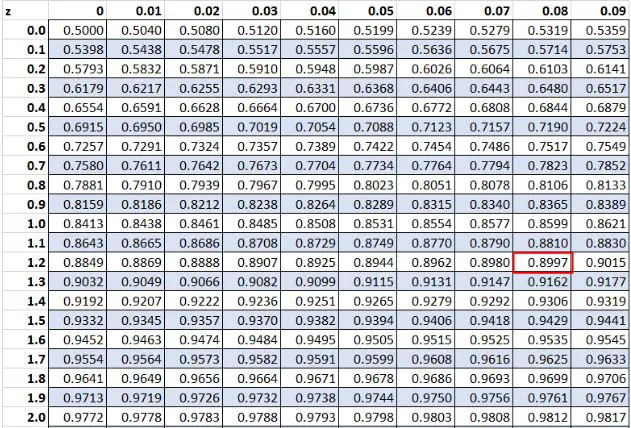
Conclusione

I punteggi Z possono assumere qualsiasi valore compreso tra infinito negativo e infinito positivo, ma la maggior parte dei punteggi Z rientra entro 2 deviazioni standard dalla media. In realtà esiste una regola statistica nota come regola pratica , che afferma che per un dato set di dati con una distribuzione normale:

• Il 68% dei valori dei dati rientra in una deviazione standard dalla media.
• Il 95% dei valori dei dati si trova entro due deviazioni standard dalla media.
• Il 99,7% dei valori dei dati rientra nelle tre deviazioni standard della media.

Maggiore è il valore assoluto di un punteggio z, maggiore è la distanza del valore grezzo dalla media del set di dati. Più basso è il valore assoluto di un punteggio z, più il valore grezzo si avvicina alla media del set di dati.

Argomenti correlati:

Calcolatore delle regole del pollice
Come applicare la regola pratica in Excel