Come calcolare il valore atteso di x^2

Per una variabile casuale , denominata X, è possibile utilizzare la seguente formula per calcolare il valore atteso di X ² :

E( ^X2 ) = ^Σx2 * p(x)

Oro:

• Σ : Un simbolo che significa “somma”
• x : il valore della variabile casuale
• p(x) : La probabilità che la variabile casuale assuma un dato valore

L’esempio seguente mostra come utilizzare questa formula nella pratica.

Esempio: calcolo del valore atteso di X ²

Supponiamo di avere la seguente tabella di distribuzione di probabilità che descrive la probabilità che una variabile casuale,

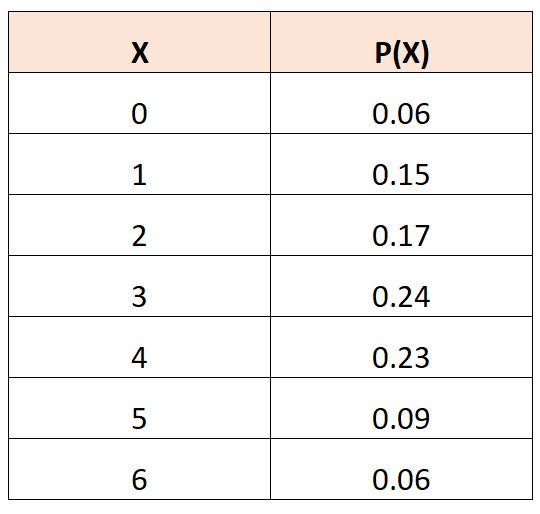
Per calcolare il valore atteso di X ² , possiamo utilizzare la seguente formula:

E( ^X2 ) = ^Σx2 * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

E( ^X2 ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16

E( ^X2 ) = 11.08

Il valore atteso di X ² è 11.08 .

Nota che questa variabile casuale è una variabile casuale discreta , il che significa che può assumere solo un numero finito di valori.

Se X è una variabile casuale continua , dobbiamo utilizzare la seguente formula per calcolare il valore atteso di X ² :

E(X ² ) = ∫ x ² f(x)dx

Oro:

• ∫: Un simbolo che significa “integrazione”
• f(x) : La pdf continua per la variabile casuale

Quando calcoliamo il valore atteso di ^X2 per una variabile casuale continua, in genere utilizziamo un software statistico perché questo calcolo può essere più difficile da eseguire manualmente.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni nelle statistiche:

Come trovare la media di una distribuzione di probabilità
Come trovare la deviazione standard di una distribuzione di probabilità
Come trovare la varianza di una distribuzione di probabilità