Come calcolare il valore atteso di x^3

Per una variabile casuale , denominata X, è possibile utilizzare la seguente formula per calcolare il valore atteso di X ³ :

E( ^X3 ) = ^Σx3 * p(x)

Oro:

• Σ : Un simbolo che significa “somma”
• x : il valore della variabile casuale
• p(x) : La probabilità che la variabile casuale assuma un dato valore

L’esempio seguente mostra come utilizzare questa formula nella pratica.

Esempio: Calcolo del valore atteso di X ³

Supponiamo di avere la seguente tabella di distribuzione di probabilità che descrive la probabilità che una variabile casuale,

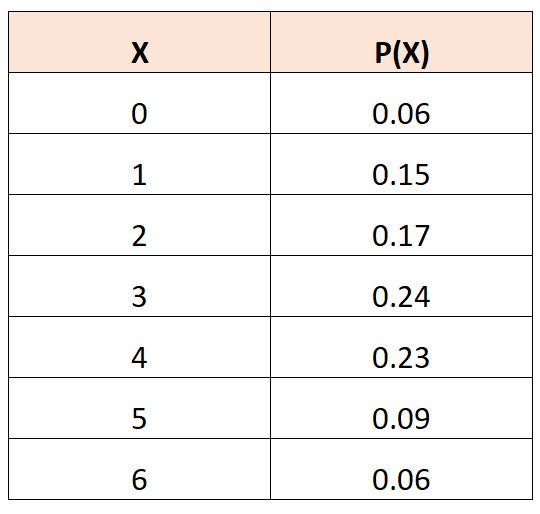
Per calcolare il valore atteso di X ³ , possiamo utilizzare la seguente formula:

E( ^X3 ) = ^Σx3 * p(x)

E(X ³ ) = (0) ³ *.06 + (1) ³ *.15 + (2) ³ *.17 + (3) ³ *.24 + (4) ³ *.23 + (5) ³ *.09 + (6) ³ *.06

E( ^X3 ) = 0 + 0,15 + 0,1,36 + 6,48 + 14,72 + 11,25 + 12,96

E( ^X3 ) = 45.596

Il valore atteso di X ³ è 45.596 .

Nota che questa variabile casuale è una variabile casuale discreta , il che significa che può assumere solo un numero finito di valori.

Se X è una variabile casuale continua , dobbiamo utilizzare la seguente formula per calcolare il valore atteso di X ³ :

E(X ³ ) = ∫ x ³ f(x)dx

Oro:

• ∫: Un simbolo che significa “integrazione”
• f(x) : La pdf continua per la variabile casuale

Quando si calcola il valore atteso ^di

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni nelle statistiche:

Come trovare la media di una distribuzione di probabilità
Come trovare la deviazione standard di una distribuzione di probabilità
Come trovare la varianza di una distribuzione di probabilità