Valore critico

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega qual è il valore critico nelle statistiche e come dovrebbe essere interpretato nei test di ipotesi. Allo stesso modo potrete vedere come viene calcolato il valore critico e alcuni esempi concreti.

Qual è il valore critico?

Il valore critico è il punto nella distribuzione della statistica test che separa la regione di rifiuto dell’ipotesi nulla dalla sua regione di accettazione. In altre parole, il valore critico è il valore della distribuzione del test statistico che segna il limite della regione di rigetto (o regione critica).

Normalmente il valore critico è rappresentato dal simbolo Z _α/2 , poiché la distribuzione di riferimento più comune è solitamente la distribuzione normale standard .

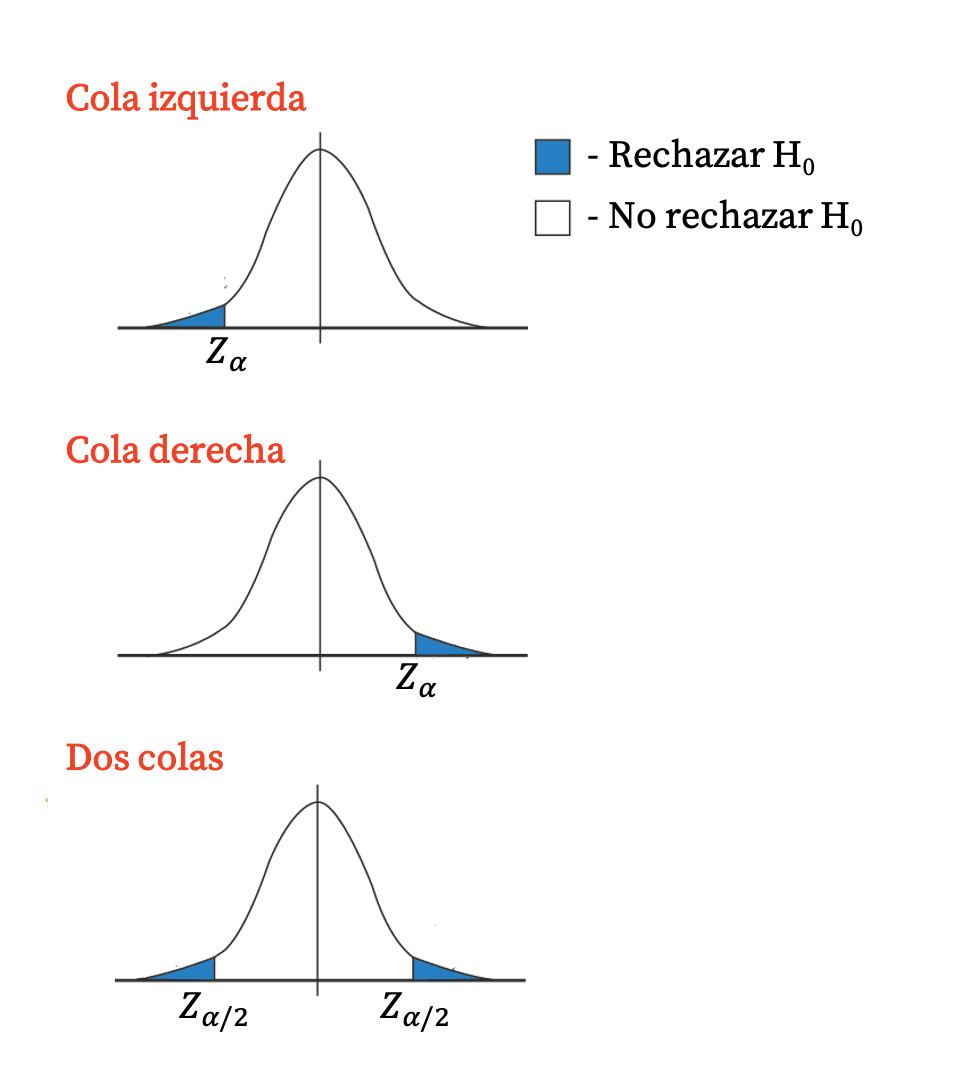
In generale, i test unilaterali hanno un valore critico, poiché la regione di rifiuto costituisce un’unica coda della distribuzione. D’altra parte, i test a due code hanno due valori critici, perché la regione di rifiuto corrisponde ad entrambe le code della distribuzione.

Negli intervalli di confidenza , i valori critici sono i punti nella distribuzione di riferimento che segnano i limiti dell’intervallo di confidenza.

Come calcolare il valore critico

Vedremo poi come vengono calcolati i valori critici più comuni. Il valore critico di Z e il valore critico di t vengono calcolati per l’intervallo di confidenza della media, l’unica differenza è che il valore critico di Z viene calcolato quando la deviazione standard della popolazione è nota e invece viene utilizzato il valore critico di t quando sono noti solo i dati di un campione.

Valore critico di Z

Il valore critico di Z viene utilizzato per determinare i limiti dell’intervallo di confidenza per la media. Più precisamente, viene utilizzato solo se si conosce la deviazione standard della popolazione.

Per calcolare il valore critico di Z, è necessario trovare nella tabella della distribuzione normale standard il valore corrispondente alla probabilità della metà del livello di significatività.

Ad esempio, se vogliamo determinare un intervallo di confidenza per la media con un livello di confidenza del 95%, ciò implica che il livello di significatività è del 5%. Pertanto è necessario vedere nella tabella della distribuzione normale standard quale valore corrisponde ad una probabilità del 2,5%, poiché l’intervallo di confidenza per la media è bilaterale.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Di seguito puoi vedere una tabella con i valori Z critici più utilizzati:

Livello di confidenza (1-α)	Livello di significatività (α)	Valore critico (Z _α/2 )
0,80	0,20	1.282
0,85	0,15	1.440
0,90	0,10	1.645
0,95	0,05	1960
0,99	0,01	2.576
0,995	0,005	2.807
0,999	0,001	3.291

Valore critico di t

Il valore t critico viene utilizzato per trovare i limiti dell’intervallo di confidenza per la media quando la deviazione standard della popolazione non è nota.

Per calcolare il valore critico di t, è necessario trovare nella tabella della distribuzione t di Student il valore corrispondente alla probabilità della metà del livello di significatività, tenendo conto che i gradi di libertà della distribuzione t di Student sono unitari. rispetto alla dimensione del campione.

Ad esempio, se vogliamo trovare l’intervallo di confidenza con un livello di confidenza del 95% e la dimensione del campione è 8, dobbiamo accedere alla tabella di distribuzione t di Student e vedere quale valore corrisponde a t _0.025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Vedi: Come calcolare l’intervallo di confidenza della media

Il valore critico nella verifica delle ipotesi

Il valore critico può essere utilizzato anche nella verifica delle ipotesi per rifiutare l’ipotesi nulla (e accettare l’ipotesi alternativa) o rifiutare l’ipotesi alternativa (e accettare l’ipotesi nulla).

Se il valore della distribuzione della statistica test corrispondente al valore p rientra nell’intervallo contrassegnato dai valori critici, l’ipotesi nulla non viene rifiutata (viene rifiutata l’ipotesi alternativa).
Se il valore della distribuzione della statistica test corrispondente al valore p è esterno all’intervallo contrassegnato dai valori critici, l’ipotesi nulla viene rifiutata (viene accettata l’ipotesi alternativa).

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più