Come trovare un valore p da un punteggio t in excel

Spesso in statistica, un test di ipotesi risulterà in una statistica di test T-score. Una volta trovato il punteggio t, di solito troviamo il valore p ad esso associato. Se questo valore p è inferiore a un certo livello alfa (ad esempio 0,10, 0,05, 0,01), allora rifiutiamo l’ipotesi nulla del test e concludiamo che i nostri risultati sono significativi.

Questo tutorial spiega come trovare il valore p da un punteggio t in Excel utilizzando la funzione DISTRIB.T , che accetta i seguenti argomenti:

DISTRIB.T (x, gradi_libertà)

Oro:

• x: il punteggio T che ci interessa.
• deg_freedom: i gradi di libertà.

Vediamo alcuni esempi.

Esempio 1: valore P dal punteggio t (a due code)

Un botanico vuole sapere se l’altezza media di una certa specie di piante è pari a 15 pollici. In un campione casuale di 12 piante, scopre che l’altezza media del campione è di 14,33 pollici e la deviazione standard del campione è di 1,37 pollici.

Esegui un test di ipotesi a due code utilizzando un livello alfa di 0,05 per determinare se l’altezza media è pari a 15 pollici.

Passaggio 1: formulare le ipotesi.

L’ipotesi nulla (H ₀ ): μ = 15

L’ipotesi alternativa: (Ha): μ ≠ 15

Passaggio 2: Trova il punteggio T e i gradi di libertà.

punteggio t = ( x -μ) / (s/√n) = (14,33-15) / (1,37/√12) = -1,694 .

gradi di libertà = n-1 = 12-1 = 11 .

Passaggio 3: trova il valore p del punteggio t utilizzando Excel.

Per trovare il valore p del punteggio t, utilizzeremo la seguente formula in Excel:

=DIST.T.2T(ABS(-1.694), 11)

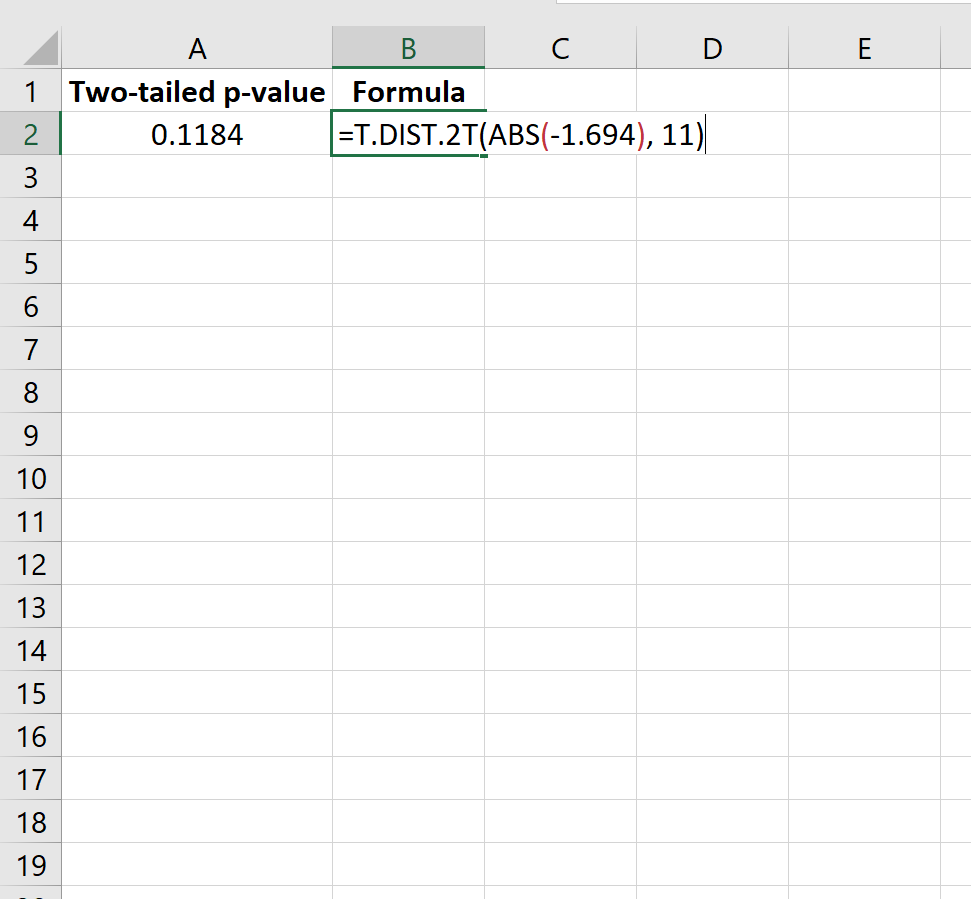
Questo ci dice che il valore p bilaterale è 0,1184 .

Passaggio 4: rifiutare o non rifiutare l’ipotesi nulla.

Poiché il valore p di 0,1184 non è inferiore al livello alfa scelto di 0,05 , non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che l’altezza media delle piante sia diversa da 15 pollici.

Esempio 2: valore P dal punteggio T (unilaterale)

Un’azienda vuole sapere se un nuovo tipo di batteria ha una durata media più lunga rispetto all’attuale batteria standard, che ha una durata media di 18 ore. In un campione casuale di 25 batterie nuove, hanno scoperto che la durata media è di 19 ore con una deviazione standard di 4 ore.

Eseguire un test di ipotesi unilaterale utilizzando un livello alfa di 0,05 per determinare se la durata media della nuova batteria è più lunga della durata media dell’attuale batteria standard.

Passaggio 1: formulare le ipotesi.

L’ipotesi nulla (H ₀ ): μ ≤ 18

Ipotesi alternativa: (Ha): μ > 18

Passaggio 2: Trova il punteggio T e i gradi di libertà.

punteggio t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .

gradi di libertà = n-1 = 25-1 = 24 .

Passaggio 3: trova il valore p del punteggio t utilizzando Excel.

Per trovare il valore p del punteggio t, utilizzeremo la seguente formula in Excel:

=DIST.T.RT(1,25, 24)

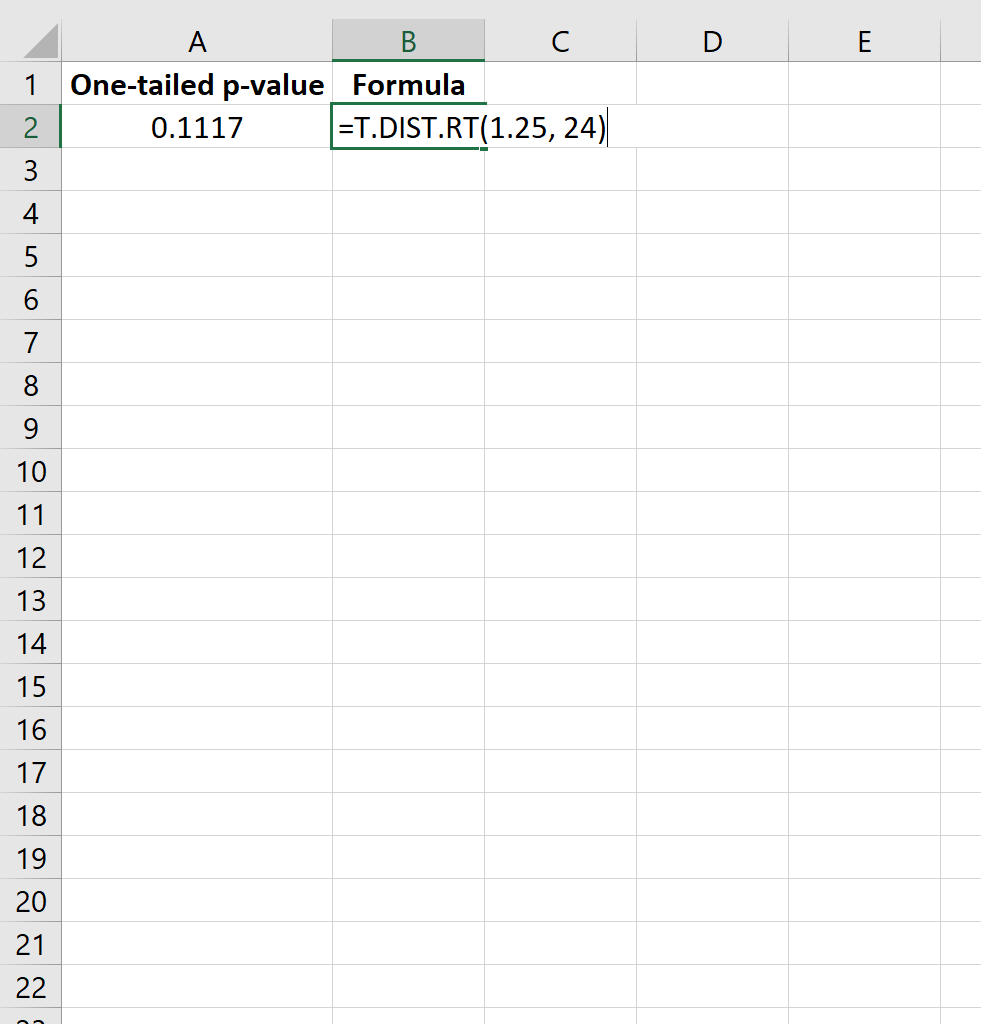
Questo ci dice che il valore p unilaterale è 0,1117 .

Passaggio 4: rifiutare o non rifiutare l’ipotesi nulla.

Poiché il valore p di 0,1117 è maggiore del livello alfa scelto di 0,05 , non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che la vita media della nuova batteria sia più lunga della vita media dell’attuale batteria standard.

Per ulteriori tutorial sulle statistiche in Excel, assicurati di consultare il nostro elenco completo di guide su Excel .