La differenza tra valori t e valori p nelle statistiche

Due termini che gli studenti spesso confondono in statistica sono valori t e valori p .

Per comprendere la differenza tra questi termini, è utile comprendere i test t .

In generale, esistono tre diversi tipi di test t:

• Test t a un campione : utilizzato per verificare se la media di una popolazione è uguale a un determinato valore.
• Test t a due campioni : utilizzato per verificare se le medie di due popolazioni sono uguali.
• Test t per campioni accoppiati : utilizzato per verificare se le medie di due popolazioni sono uguali quando ciascuna osservazione in un campione può essere associata a un’osservazione nell’altro campione.

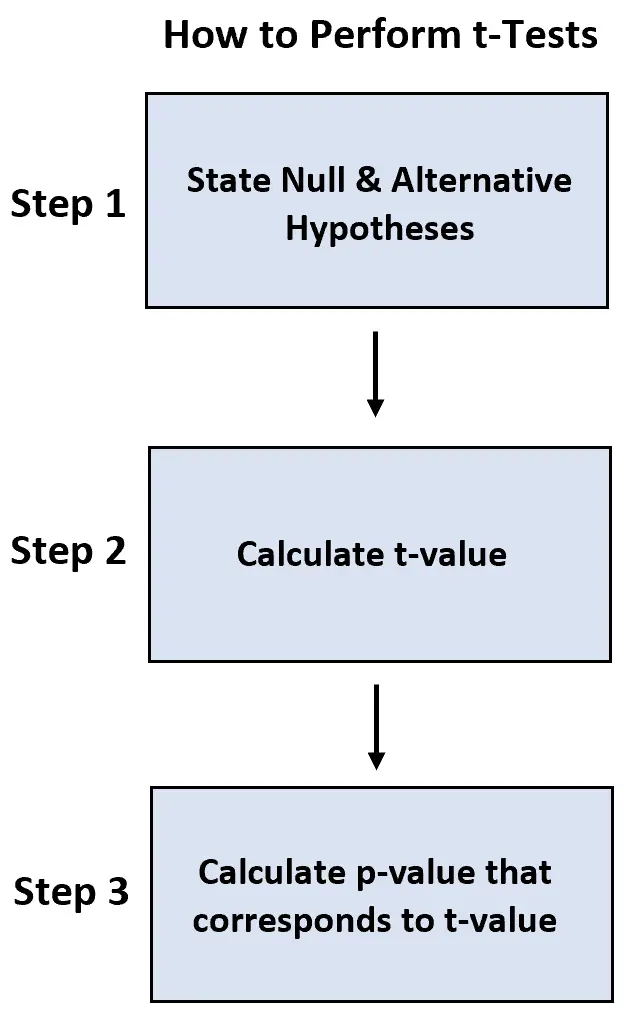
Utilizziamo i seguenti passaggi per eseguire ciascun test:

• Passaggio 1: enunciare l’ipotesi nulla e alternativa.
• Passaggio 2: calcolare il valore t.
• Passaggio 3: calcolare il valore p che corrisponde al valore t.

Per ogni test, il valore t è un modo per quantificare la differenza tra le medie della popolazione e il valore p è la probabilità di ottenere un valore t con un valore assoluto almeno pari a quello effettivamente osservato nel campione. dati se l’ipotesi nulla è effettivamente vera.

Se il valore p è inferiore a un certo valore (ad esempio 0,05), allora rifiutiamo l’ipotesi nulla del test.

Per ogni tipo di test t, siamo interessati al valore p e utilizziamo semplicemente il valore t come passaggio intermedio per calcolare il valore p.

L’esempio seguente mostra come calcolare e interpretare un valore t e il valore p corrispondente per un test t a due campioni.

Esempio: calcolare e interpretare i valori T e i valori P

Supponiamo di voler sapere se il peso medio di due diverse specie di tartarughe è uguale o meno. Raccogliamo un campione casuale semplice di 12 tartarughe da ciascuna popolazione con i seguenti pesi:

Specie n. 1 : 301, 298, 295, 297, 304, 305, 309, 298, 291, 299, 293, 304

Specie n. 2 : 302, 309, 324, 313, 312, 310, 305, 298, 299, 300, 289, 294

Ecco come eseguire un t-test a due campioni utilizzando questi dati:

Passaggio 1: enunciare l’ipotesi nulla e alternativa.

Per prima cosa enunceremo le ipotesi nulla e alternativa:

• H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)
• H ₁ : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Passaggio 2: calcolare il valore t.

Successivamente, inseriremo i pesi di ciascun campione di tartaruga nel calcolatore del test t a due campioni e scopriremo che il valore t è -1.608761 .

Passaggio 3: calcolare il valore p.

Possiamo anche utilizzare il calcolatore del test t a due campioni per scoprire che il valore p che corrisponde a un valore t di -1.608761 è 0.121926 .

Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che non abbiamo prove sufficienti per affermare che il peso medio delle tartarughe tra le due popolazioni sia diverso.

Si noti che abbiamo semplicemente utilizzato il valore t come passaggio intermedio per calcolare il valore p. Il valore p è il valore reale a cui eravamo interessati, ma dovevamo prima calcolare il valore t.

Risorse addizionali

I seguenti tutorial offrono informazioni aggiuntive sui test t e sui valori p:

Un’introduzione al t-test per un campione
Un’introduzione al test t a due campioni
Un’introduzione al t-test per campioni appaiati
Come calcolare manualmente un valore P da un test t