La differenza tra valori z e valori p nelle statistiche

Due termini che gli studenti spesso confondono in statistica sono valori z e valori p .

Per comprendere la differenza tra questi termini, è utile comprendere i test z .

Esistono due tipi comuni di test z:

• Test z a un campione : utilizzato per verificare se la media di una popolazione è uguale a un determinato valore.
• Test z a due campioni : utilizzato per verificare se le medie di due popolazioni sono uguali.

Utilizziamo i seguenti passaggi per eseguire ciascun test:

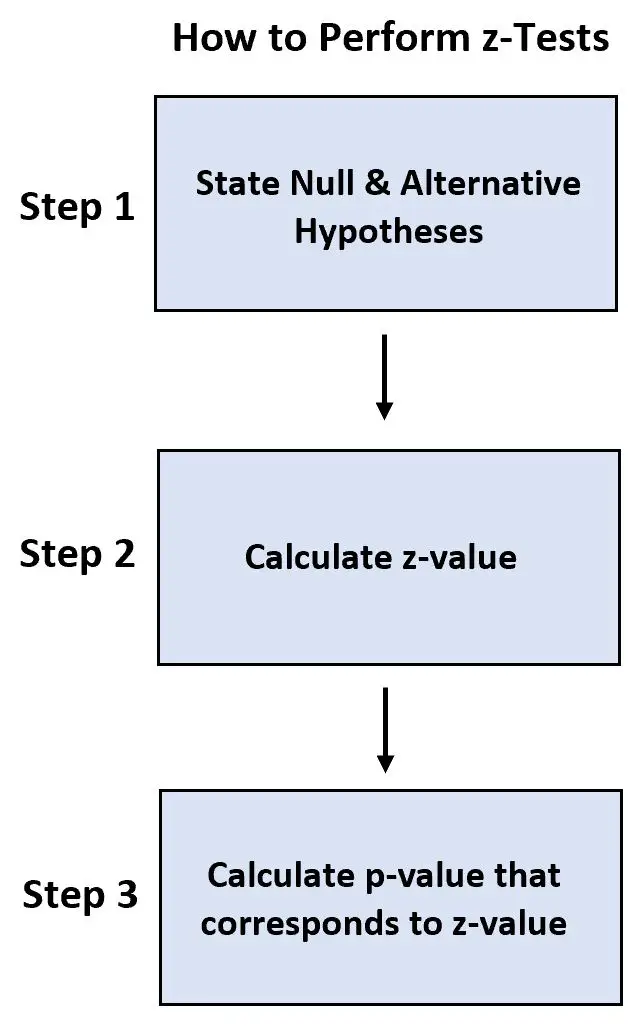
• Passaggio 1: enunciare l’ipotesi nulla e alternativa.
• Passaggio 2: calcolare il valore z.
• Passaggio 3: calcolare il valore p che corrisponde al valore z.

Per ciascun test, il valore z è un modo per quantificare la differenza tra le medie della popolazione e il valore p è la probabilità di ottenere un valore z con un valore assoluto almeno pari a quello effettivamente osservato nel campione. dati se l’ipotesi nulla è effettivamente vera.

Se il valore p è inferiore a un certo valore (ad esempio 0,05), allora rifiutiamo l’ipotesi nulla del test.

Per ogni tipo di test z, siamo interessati al valore p e utilizziamo semplicemente il valore z come passaggio intermedio per calcolare il valore p.

L’esempio seguente mostra come calcolare e interpretare un valore z e il valore p corrispondente per un test z a due campioni.

Esempio: calcolare e interpretare i valori Z e i valori P

Supponiamo che i livelli di QI degli individui di due città diverse siano distribuiti normalmente, ciascuno con deviazioni standard della popolazione pari a 15.

Uno scienziato vuole sapere se il livello medio di QI tra gli individui della città A e della città B è diverso. Seleziona quindi un semplice campione casuale di 20 individui da ciascuna città e registra i loro livelli di QI:

Città A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Città B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

Ecco come eseguire un test z a due campioni utilizzando questi dati:

Passaggio 1: enunciare l’ipotesi nulla e alternativa.

Per prima cosa enunceremo le ipotesi nulla e alternativa:

• H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)
• H ₁ : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Passaggio 2: calcolare il valore z.

Successivamente, eseguiremo un test z a due campioni in Excel utilizzando questi dati e scopriremo che il valore z è -1.71817 .

Passaggio 3: calcolare il valore p.

Possiamo utilizzare il calcolatore del punteggio Z per il valore P per scoprire che il valore p che corrisponde al valore az di -1,71817 è 0,08577.

Poiché questo valore p non è inferiore a 0,05, non abbiamo prove sufficienti per rifiutare l’ipotesi nulla.

Pertanto, concludiamo che il livello medio del QI non è significativamente diverso tra le due città.

Tieni presente che abbiamo semplicemente utilizzato il valore z come passaggio intermedio per calcolare il valore p.

Il valore p è il valore reale a cui eravamo interessati, ma dovevamo prima calcolare il valore z.

Risorse addizionali

I seguenti tutorial spiegano come eseguire z-test utilizzando vari software statistici:

Come eseguire test Z in Excel
Come eseguire i test Z in R
Come eseguire i test Z in Python