Cos'è una variabile confusa? (definizione & #038; esempio)

In ogni esperimento, ci sono due variabili principali:

La variabile indipendente: la variabile che uno sperimentatore modifica o controlla per poter osservare gli effetti sulla variabile dipendente.

La variabile dipendente: la variabile misurata in un esperimento che è “dipendente” dalla variabile indipendente.

I ricercatori sono spesso interessati a capire come i cambiamenti nella variabile indipendente influenzano la variabile dipendente.

Tuttavia, a volte accade che una terza variabile non venga presa in considerazione e che questa possa influenzare la relazione tra le due variabili studiate.

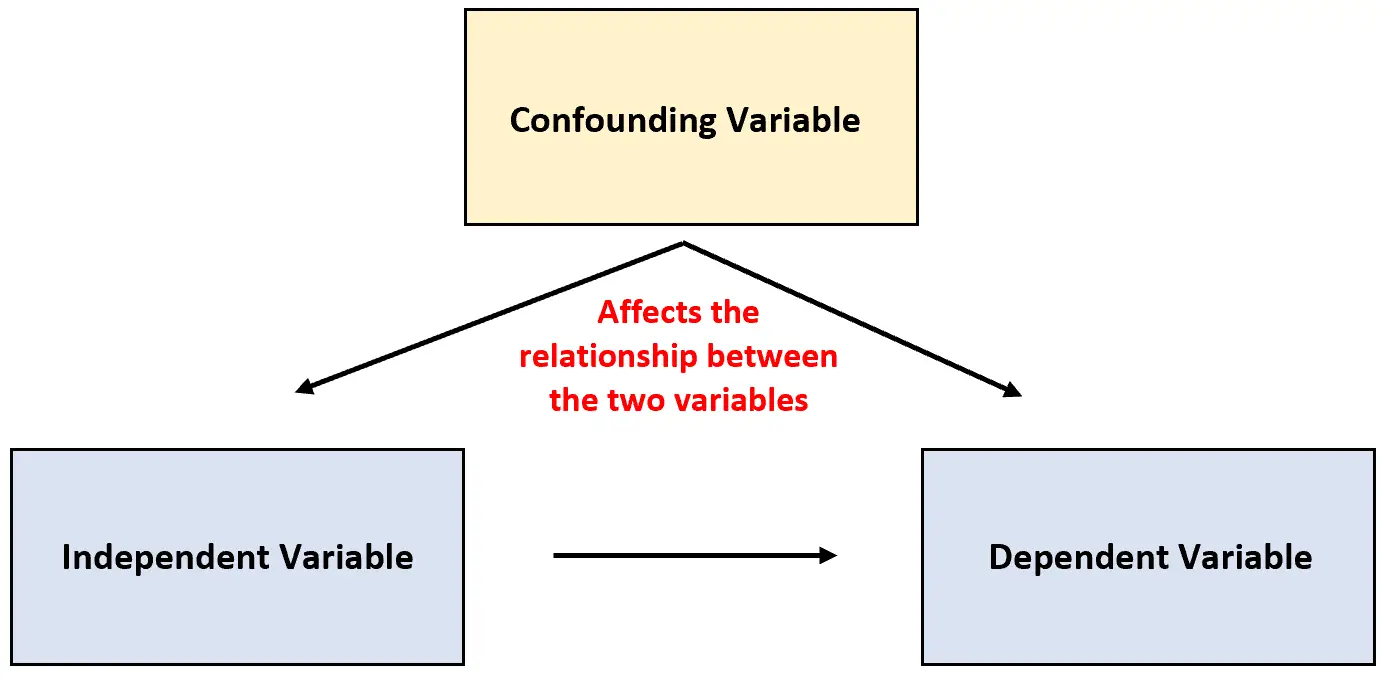
Questo tipo di variabile è nota come variabile di confondimento e può confondere i risultati di uno studio e far sembrare che esista un qualche tipo di relazione di causa ed effetto tra due variabili che in realtà non esiste.

Variabile di confondimento: una variabile che non è inclusa in un esperimento, ma influenza la relazione tra le due variabili in un esperimento.

Questo tipo di variabile può confondere i risultati di un esperimento e portare a risultati inaffidabili.

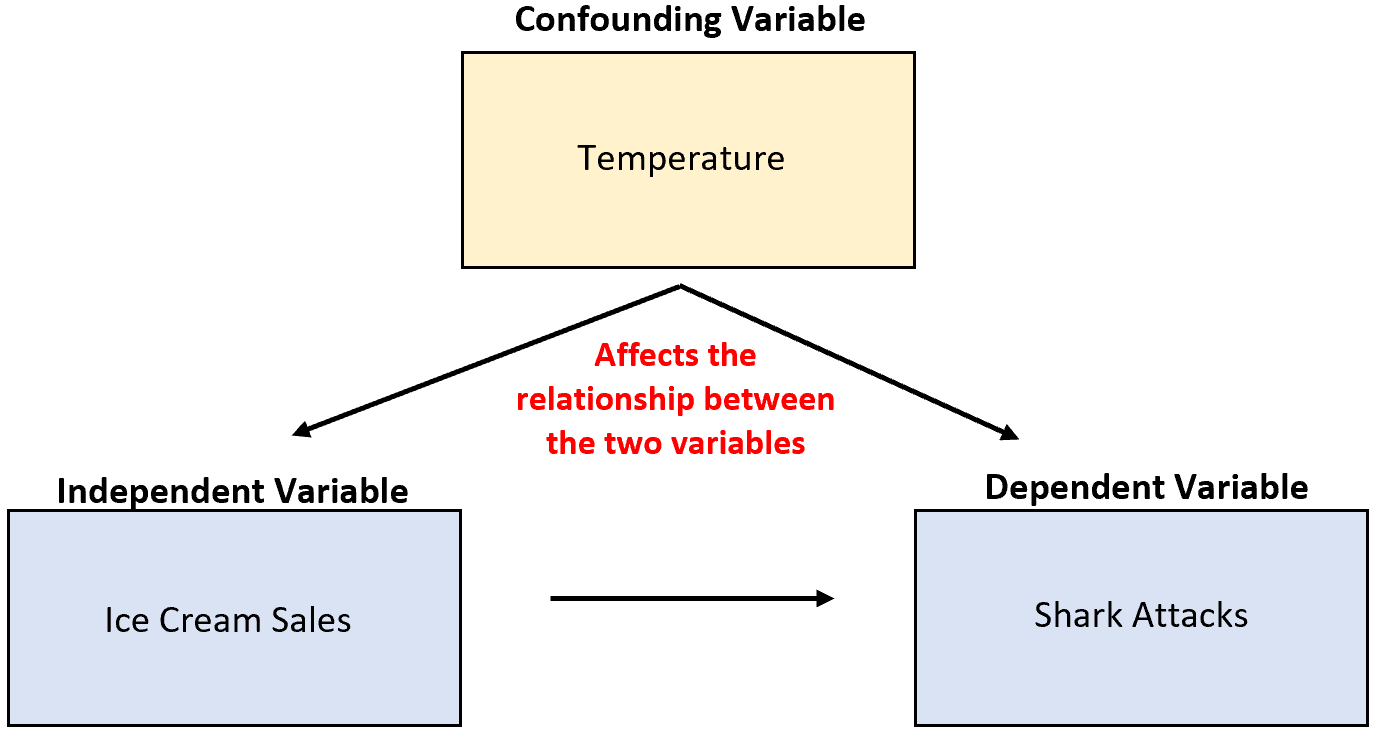
Ad esempio, supponiamo che un ricercatore raccolga dati sulle vendite di gelati e sugli attacchi di squali e scopra che le due variabili sono altamente correlate. Ciò significa che l’aumento delle vendite di gelati sta causando più attacchi di squali?

E ‘improbabile. La causa più probabile è la confusa temperatura variabile. Quando fuori fa più caldo, più persone acquistano il gelato e più persone vanno al mare.

Requisiti per le variabili confuse

Affinché una variabile possa creare confusione, deve soddisfare i seguenti requisiti:

1. Deve essere correlato con la variabile indipendente.

Nell’esempio precedente la temperatura era correlata alla variabile indipendente delle vendite di gelato. In particolare, temperature più calde sono associate a maggiori vendite di gelato e temperature più fredde a minori vendite.

2. Deve esserci una relazione causale con la variabile dipendente.

Nell’esempio precedente, la temperatura ha avuto un effetto causale diretto sul numero di attacchi di squali. In particolare, le temperature più calde spingono più persone nell’oceano, il che aumenta direttamente la probabilità di attacchi di squali.

Perché confondere le variabili è problematico?

Le variabili confondenti sono problematiche per due ragioni:

1. Le variabili confondenti possono far sembrare che esistano relazioni di causa ed effetto quando non lo sono.

Nel nostro esempio precedente, la variabile confusa della temperatura faceva sembrare che esistesse una relazione causale tra le vendite di gelati e gli attacchi di squali.

Sappiamo però che la vendita di gelati non provoca attacchi di squali. La confusa variabile della temperatura fa sembrare così.

2. Le variabili confondenti possono oscurare la vera relazione di causa ed effetto tra le variabili.

Supponiamo di studiare la capacità dell’esercizio di ridurre la pressione sanguigna. Una potenziale variabile confondente è il peso iniziale, che è correlato all’esercizio fisico e ha un effetto causale diretto sulla pressione sanguigna.

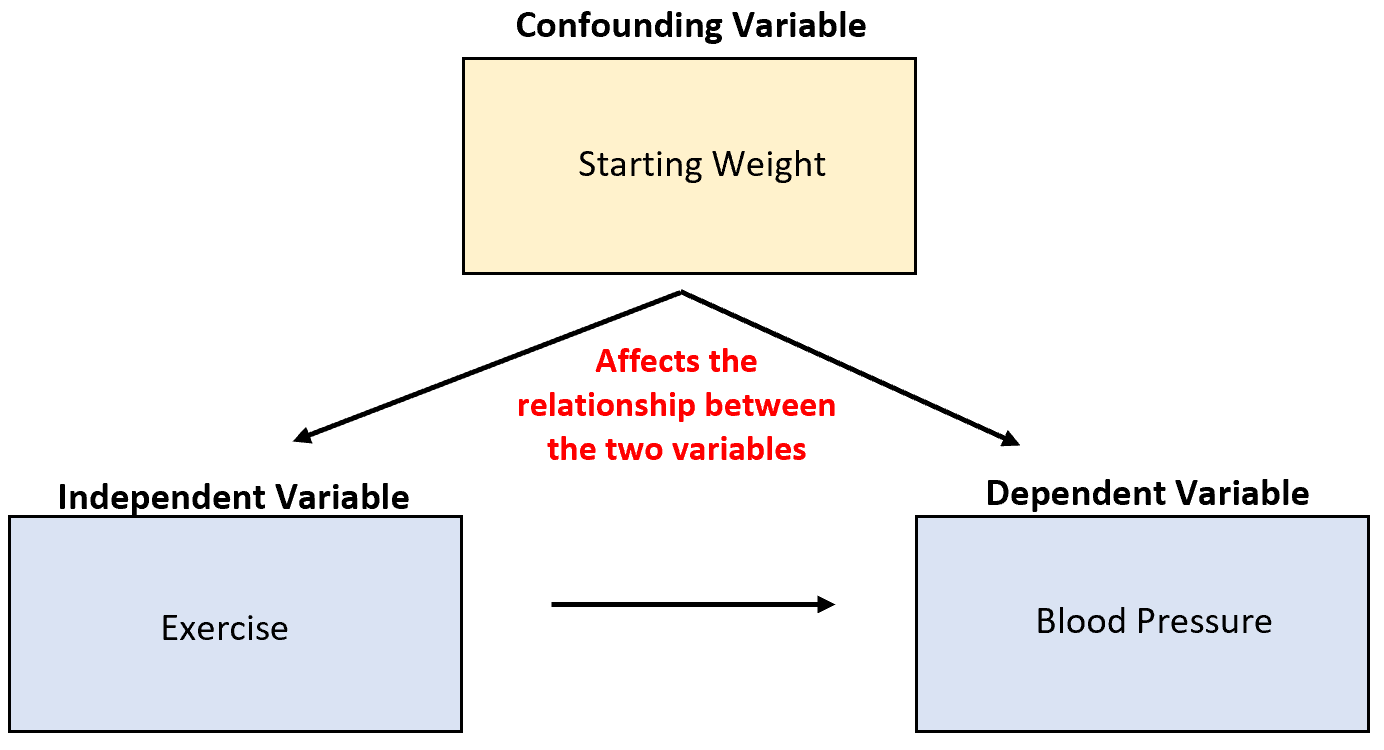
Sebbene una maggiore attività fisica possa portare ad una riduzione della pressione sanguigna, anche il peso iniziale di un individuo ha un grande impatto sulla relazione tra queste due variabili.

Variabili di confondimento e validità interna

In termini tecnici, le variabili confondenti influenzano la validità interna di uno studio, che si riferisce alla validità di attribuire eventuali cambiamenti nella variabile dipendente a cambiamenti nella variabile indipendente.

Quando sono presenti variabili confondenti, non possiamo sempre dire con certezza che i cambiamenti che osserviamo nella variabile dipendente siano il risultato diretto dei cambiamenti nella variabile indipendente.

Come ridurre l’effetto delle variabili confuse

Esistono diversi modi per ridurre l’effetto delle variabili confuse, inclusi i seguenti metodi:

1. Assegnazione casuale

L’assegnazione casuale si riferisce al processo di assegnazione casuale degli individui in uno studio a un gruppo di trattamento o a un gruppo di controllo.

Ad esempio, supponiamo di voler studiare l’effetto di una nuova pillola sulla pressione sanguigna. Se reclutiamo 100 persone per partecipare allo studio, potremmo utilizzare un generatore di numeri casuali per assegnare casualmente 50 persone a un gruppo di controllo (nessuna pillola) e 50 persone a un gruppo di trattamento (nuova pillola).

Utilizzando l’assegnazione casuale, aumentiamo la possibilità che i due gruppi abbiano caratteristiche più o meno simili, il che significa che eventuali differenze osservate tra i due gruppi possono essere attribuite al trattamento.

Ciò significa che lo studio deve avere validità interna : è valido per attribuire eventuali differenze di pressione arteriosa tra i gruppi alla pillola stessa, e non le differenze tra gli individui dei gruppi.

2. Blocco

Il blocco si riferisce alla pratica di dividere gli individui in uno studio in “blocchi” in base a un certo valore di una variabile di confondimento al fine di eliminare l’effetto della variabile di confondimento.

Ad esempio, supponiamo che i ricercatori vogliano comprendere l’effetto di una nuova dieta sulla perdita di peso. La variabile indipendente è la nuova dieta e la variabile dipendente è la quantità di perdita di peso.

Tuttavia, una variabile confondente che può causare variazioni nella perdita di peso è il sesso . È probabile che il sesso di un individuo influisca sulla quantità di peso perso, indipendentemente dal fatto che la nuova dieta funzioni o meno.

Un modo per risolvere questo problema è posizionare gli individui in uno dei due blocchi:

• Maschio
• Femmina

Quindi, all’interno di ciascun blocco, assegneremmo casualmente gli individui a uno dei due trattamenti:

• Una nuova dieta
• Una dieta standard

In questo modo, la variazione all’interno di ciascun blocco sarebbe molto inferiore alla variazione tra tutti gli individui e saremmo in grado di comprendere meglio come la nuova dieta influisce sulla perdita di peso controllando il sesso.

3. Corrispondenza

Un disegno a coppia abbinata è un tipo di disegno sperimentale in cui “abbiniamo” gli individui in base ai valori di potenziali variabili confondenti.

Ad esempio, supponiamo che i ricercatori vogliano sapere in che modo una nuova dieta influisce sulla perdita di peso rispetto a una dieta standard. Due potenziali variabili confuse in questa situazione sono l’età e il sesso .

Per tenere conto di ciò, recluta i ricercatori 100 soggetti, quindi raggruppali in 50 coppie in base alla loro età e sesso. Per esempio:

• Un uomo di 25 anni verrà abbinato a un altro uomo di 25 anni, poiché “corrispondono” in termini di età e sesso.
• Una donna di 30 anni verrà abbinata a un’altra donna di 30 anni poiché corrispondono anche in termini di età, sesso, ecc.

Quindi, all’interno di ciascuna coppia, un soggetto verrà assegnato in modo casuale a seguire la nuova dieta per 30 giorni e l’altro soggetto verrà assegnato a seguire la dieta standard per 30 giorni.

Alla fine dei 30 giorni, i ricercatori misureranno la perdita di peso totale per ciascun soggetto.

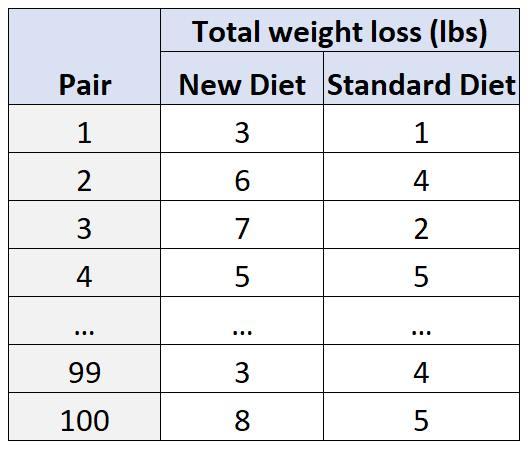
Utilizzando questo tipo di disegno, i ricercatori possono essere sicuri che eventuali differenze nella perdita di peso possono essere attribuite al tipo di dieta utilizzata piuttosto che alle variabili confondenti di età e sesso .

Questo tipo di progettazione presenta alcuni svantaggi, tra cui:

1. Perdere due soggetti se uno di loro abbandona. Se un soggetto decide di abbandonare lo studio, in realtà perdi due soggetti poiché non hai più una coppia completa.

2. Ci vuole tempo per trovare corrispondenze . Trovare argomenti che corrispondono a determinate variabili, come sesso ed età, può richiedere molto tempo.

3. Impossibile abbinare perfettamente gli argomenti . Non importa quanto ci provi, ci saranno sempre variazioni all’interno dei soggetti di ciascuna coppia.

Tuttavia, se uno studio ha le risorse disponibili per implementare questo disegno, può essere molto efficace nell’eliminare gli effetti delle variabili confondenti.