Variabile indipendente

Questo articolo spiega cosa sono le variabili indipendenti. Troverai così il significato di una variabile indipendente in matematica e statistica e vedrai anche diversi esempi di questo tipo di variabile.

Cos’è una variabile indipendente?

Una variabile indipendente è una variabile il cui valore non dipende dal valore di nessun’altra variabile. Al contrario, se una variabile indipendente cambia il suo valore, cambia il valore di una variabile dipendente.

Quando si rappresenta graficamente una variabile indipendente, solitamente è rappresentata dalla lettera x e sull’asse x (asse orizzontale).

Ad esempio, il periodo di tempo in cui affitti una proprietà è una variabile indipendente che influisce sul prezzo da pagare. Perché la durata del noleggio si può decidere e il suo valore incide sulla variabile dipendente dal prezzo, poiché più a lungo si utilizzano gli impianti, più si dovrà pagare.

Le variabili indipendenti possono anche essere chiamate variabili esplicative, variabili di input o variabili manipolate.

Esempi di variabili indipendenti

Avendo visto la definizione di variabile indipendente, vediamo ora alcuni esempi di questo tipo di variabile per comprendere meglio il concetto.

• Il tempo dedicato allo studio (variabile indipendente) incide sui voti ottenuti (variabile dipendente).
• Il prezzo di un prodotto (variabile indipendente) modifica il numero di persone disposte ad acquistare il prodotto (variabile dipendente).
• La temperatura ambiente (variabile indipendente) influenza il numero di incendi boschivi (variabile dipendente).
• La pubblicità effettuata per un prodotto (variabile indipendente) incide sul numero di vendite di tale prodotto (variabile dipendente).
• Il numero di abitanti di una città (variabile indipendente) è legato al numero di taxi presenti in una città (variabile dipendente).

Variabile indipendente in matematica

In matematica, una relazione di causa ed effetto viene solitamente modellata utilizzando una variabile indipendente e una variabile dipendente. Pertanto, una funzione definisce la relazione matematica che esiste tra la variabile indipendente e la variabile dipendente.

Le variabili indipendenti sono solitamente rappresentate dalla lettera x , mentre la lettera y viene utilizzata per le variabili dipendenti.

Ad esempio, la funzione y=2x indica che quando la variabile indipendente x aumenta di un’unità, la variabile dipendente y aumenta del doppio.

Per saperne di più sulle funzioni matematiche, ti consigliamo di visitare il nostro sito web partner function.xyz .

Variabili indipendenti in statistica

Tuttavia, in realtà, è molto difficile trovare una relazione tra due variabili che possa essere definita da una funzione matematica esatta, perché a volte lo stesso valore di una variabile indipendente risulta in un diverso valore della variabile dipendente.

Ad esempio, a volte studiando di più otteniamo un voto più basso o, al contrario, studiando di meno otteniamo un voto migliore. Quindi il numero di ore che dedichiamo allo studio non è l’unico fattore che influenza il voto ottenuto, può variare anche a seconda della difficoltà dell’esame o della difficoltà della materia studiata.

Pertanto, in statistica, molti esperimenti vengono solitamente eseguiti per determinare se esiste una relazione tra una variabile indipendente e una variabile dipendente. I risultati ottenuti possono poi essere rappresentati graficamente per verificare se le variabili sono collegate e, in caso affermativo, vedere che tipo di relazione hanno (positiva, negativa, lineare, esponenziale, ecc.).

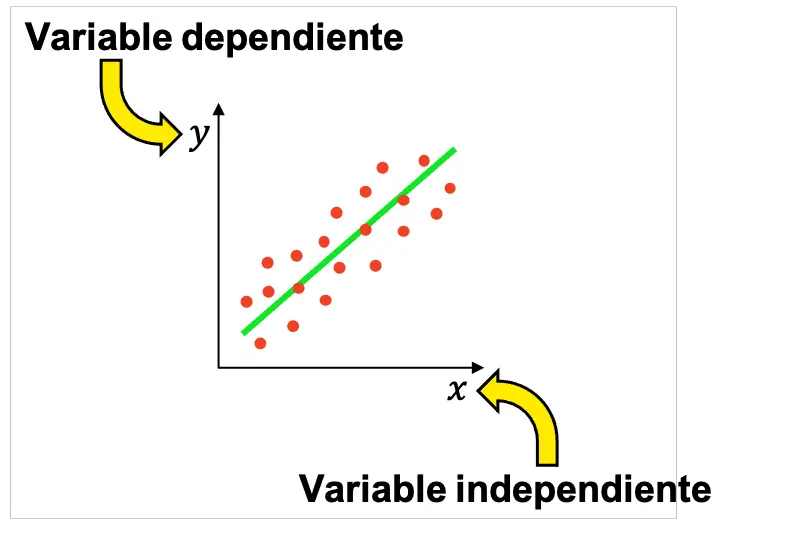
Tieni presente che in un sondaggio può essere presente più di una variabile indipendente, sebbene gli studi statistici più elementari siano condotti con una variabile indipendente e una variabile dipendente.

Una volta effettuato lo studio statistico si può calcolare una funzione matematica che permette di fare un’approssimazione e modellare così la relazione tra le variabili. Quindi normalmente si crea prima un modello statistico, poi un modello matematico.