Cosa sono le variabili casuali?

Una variabile casuale , generalmente indicata con X, è una variabile i cui possibili valori sono il risultato di un processo casuale.

Esistono due tipi di variabili casuali: discrete e continue .

Variabili casuali discrete

Una variabile casuale discreta è quella che può assumere solo un numero numerabile di valori distinti come 0, 1, 2, 3, 4, 5…100, 1 milione, ecc. Ecco alcuni esempi di variabili casuali discrete:

• Il numero di volte in cui una moneta esce croce dopo essere stata lanciata 20 volte.
• Il numero di volte in cui un dado si ferma sul numero 4 dopo essere stato lanciato 100 volte.
• Il numero di widget difettosi in una scatola da 50 widget.

Una distribuzione di probabilità per una variabile casuale discreta ci dice la probabilità che la variabile casuale assuma determinati valori.

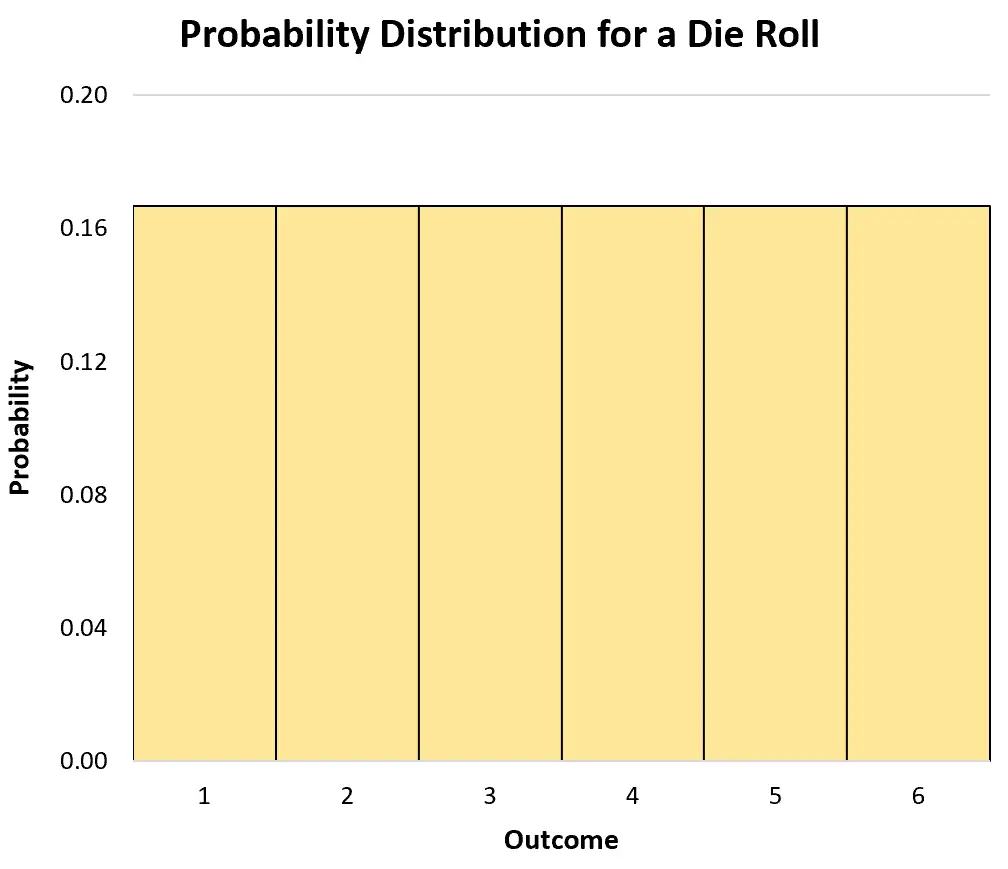
Ad esempio, supponiamo di lanciare un dado equilibrato una volta. Se indichiamo con X la probabilità che il dado esca su un certo numero, allora la distribuzione di probabilità può essere scritta come segue:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Nota:

Affinché una distribuzione di probabilità sia valida, deve soddisfare i seguenti due criteri:

1. La probabilità di ciascun risultato deve essere compresa tra 0 e 1.

2. La somma di tutte le probabilità deve dare come risultato 1.

Si noti che la distribuzione di probabilità del tiro di dado soddisfa entrambi questi criteri:

1. La probabilità di ciascun risultato è compresa tra 0 e 1.

2. La somma di tutte le probabilità dà come risultato 1.

Possiamo usare un istogramma per visualizzare la distribuzione di probabilità:

Una distribuzione di probabilità cumulativa per una variabile casuale discreta ci dice la probabilità che la variabile assuma un valore uguale o inferiore a un determinato valore.

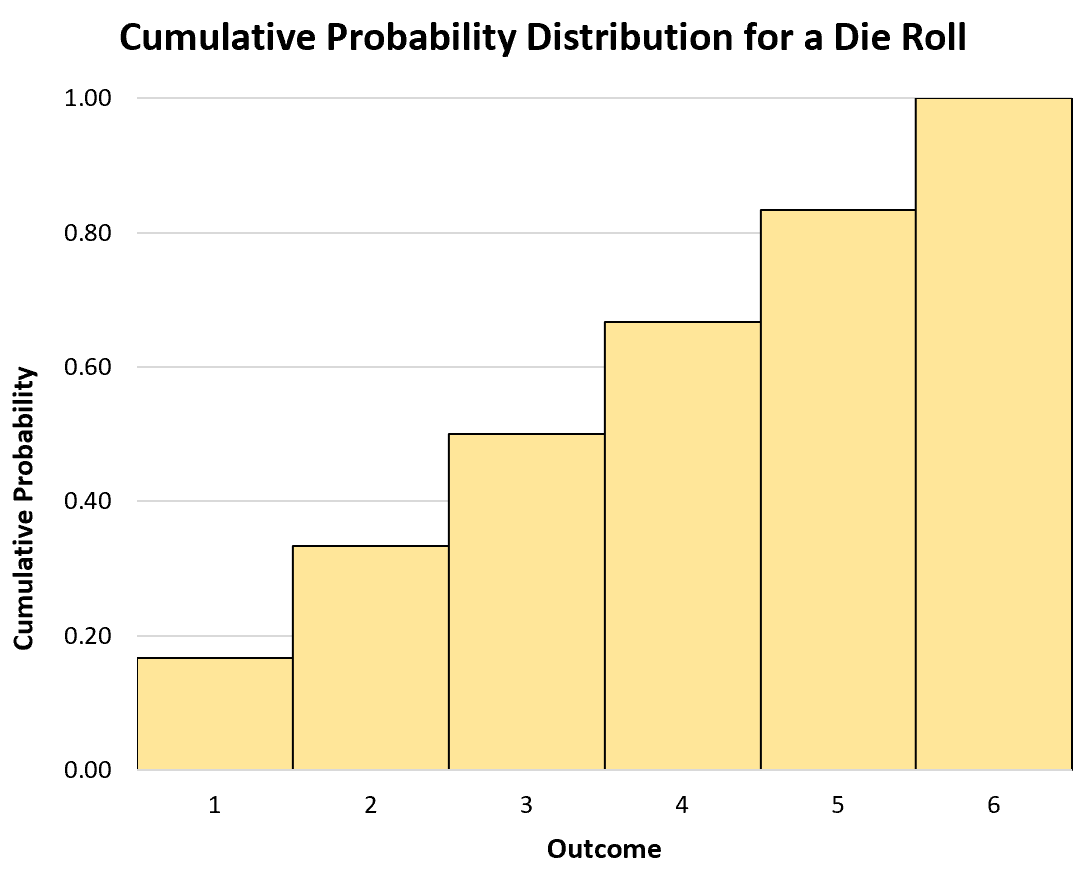
Ad esempio, la distribuzione di probabilità cumulativa per un lancio di dado sarebbe:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

La probabilità che il dado esca su uno o meno è semplicemente 1/6, poiché non può atterrare su un numero inferiore a uno.

La probabilità che arrivi su due o meno è P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Allo stesso modo, la probabilità che arrivi a tre o meno è P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, e Presto.

Possiamo anche utilizzare un istogramma per visualizzare la distribuzione di probabilità cumulativa:

Variabili casuali continue

Una variabile casuale continua è una variabile che può assumere infiniti valori possibili. Ecco alcuni esempi di variabili casuali continue:

• Peso di un animale
• Altezza di una persona
• Tempo necessario per correre una maratona

Ad esempio, l’altezza di una persona potrebbe essere 60,2 pollici, 65,2344 pollici, 70,431222 pollici, ecc. Esistono infiniti valori possibili per la dimensione.

Regola generale:

Se riesci a contare il numero di risultati, allora stai lavorando con una variabile casuale discreta, ad esempio contando il numero di volte in cui una moneta esce testa.

Ma se puoi misurare il risultato, stai lavorando con una variabile casuale continua, ad esempio misurando altezza, peso, tempo, ecc.

Una distribuzione di probabilità per una variabile casuale continua ci dice la probabilità che la variabile casuale assuma determinati valori.

Tuttavia, a differenza di una distribuzione di probabilità per variabili casuali discrete, una distribuzione di probabilità per una variabile casuale continua può essere utilizzata solo per dirci la probabilità che la variabile assuma un intervallo di valori.

Ad esempio, supponiamo di voler conoscere la probabilità che un hamburger di un particolare ristorante pesi un quarto di libbra (0,25 libbre). Poiché il peso è una variabile continua, può assumere un numero infinito di valori.

Ad esempio, un dato hamburger potrebbe effettivamente pesare 0,250001 libbre, o 0,24 libbre, o 0,2488 libbre. La probabilità che un dato hamburger peserà esattamente 0,25 libbre è essenzialmente zero.

Quindi possiamo usare solo una distribuzione di probabilità per dirci la probabilità che un hamburger pesi meno di 0,25 libbre, più di 0,25 libbre, o compreso in un certo intervallo (ad esempio tra 0,23 libbre e 0,27 libbre).

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulle variabili casuali:

Cosa sono le variabili casuali iid?
10 esempi di variabili casuali nella vita reale