Verifica di ipotesi per la varianza

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è il test di ipotesi per la varianza. Troverai quindi la formula per verificare l’ipotesi di varianza e, inoltre, un esercizio risolto passo dopo passo.

Cos’è il test di ipotesi per la varianza?

Il test di ipotesi per la varianza è un metodo statistico utilizzato per determinare se rifiutare o meno l’ipotesi nulla della varianza di una popolazione. In altre parole, il test dell’ipotesi di varianza viene utilizzato per rifiutare o accettare l’ipotesi sul valore della varianza di una popolazione.

Nello specifico, a seconda del valore della statistica del test di ipotesi per la varianza e del livello di significatività scelto, l’ipotesi nulla viene rifiutata o accettata.

Tieni presente che il test di ipotesi ha molti nomi, può anche essere chiamato contrasto di ipotesi, test di ipotesi o test di significatività.

Formula di verifica delle ipotesi per la varianza

La statistica del test di ipotesi per la varianza è uguale alla differenza tra la dimensione del campione meno una volta la varianza del campione e divisa per il valore proposto della varianza della popolazione. La statistica del test di ipotesi per la varianza ha una distribuzione chi-quadrato .

Pertanto, la formula per calcolare la statistica del test di ipotesi per la varianza è la seguente:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Oro:

$\chi^2$

è l’ipotesi che verifica la statistica della varianza, che ha una distribuzione chi-quadrato.
$n$

è la dimensione del campione.
$s^2$

è la varianza campionaria.
$\sigma^2$

è la varianza della popolazione proposta.

Per interpretare il risultato della statistica, il valore ottenuto deve essere confrontato con il valore critico del test.

Se il test di ipotesi per la varianza è a due code, l’ipotesi nulla viene rifiutata se la statistica è maggiore del valore critico.
$\chi_{1-\alpha/2|n-1}^2$

o se il valore critico è inferiore a

$\chi_{\alpha/2|n-1}$

.
Se il test di ipotesi per la varianza corrisponde alla coda destra, l’ipotesi nulla viene rifiutata se la statistica è maggiore del valore critico
$\chi_{1-\alpha|n-1}^2$

.
Se il test di ipotesi per la varianza corrisponde alla coda sinistra, l’ipotesi nulla viene rifiutata se la statistica è inferiore al valore critico
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

I valori del test dell’ipotesi critica per la varianza sono ottenuti dalla tabella di distribuzione del chi-quadrato. Si noti che i gradi di libertà per la distribuzione Chi-quadrato sono la dimensione del campione meno 1.

Esempio reale di verifica di ipotesi per la varianza

Dopo aver visto la definizione di verifica dell’ipotesi di varianza e qual è la sua formula, vedremo un esempio concreto per finire di assimilare il concetto.

Una fabbrica ha una macchina che produce parti di un’auto con alta precisione. Si sospetta però che si sia allontanata e che ora produca pezzi con uno spazio maggiore di 8 mm ² . Per confutare questa ipotesi, viene analizzato un campione di 25 pezzi e la sua varianza campionaria è di 9,1 mm ² . L’ipotesi iniziale può essere rifiutata con un livello di significatività α=0,05?

L’ipotesi nulla e l’ipotesi alternativa per questo test dell’ipotesi della varianza sono le seguenti:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Per determinare se l’ipotesi nulla può essere rifiutata o meno, calcoliamo la statistica del test di ipotesi per la varianza utilizzando la formula che abbiamo visto sopra: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Cerchiamo ora il valore critico corrispondente alla coda destra per 24 gradi di libertà e un livello di significatività α=0,05 nella tabella di distribuzione del Chi-quadrato:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Pertanto, la statistica calcolata è inferiore al valore critico del test e quindi l’ipotesi nulla del test dell’ipotesi della varianza non viene rifiutata, ma piuttosto viene rifiutata l’ipotesi alternativa.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Vedi: Verifica di ipotesi per la media della popolazione
➤ Vedi: Verifica di ipotesi per la proporzione della popolazione

Verifica di ipotesi per la varianza di due popolazioni

Il test dell’ipotesi della varianza tra due popolazioni viene utilizzato per rifiutare o accettare l’ipotesi che le varianze di due popolazioni diverse siano uguali.

Pertanto l’ipotesi nulla di un test di ipotesi sulla varianza di due popolazioni è sempre la seguente:

$H_0: \sigma^2_1=\sigma^2_2$

E l’ipotesi alternativa può essere una delle tre opzioni:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

In questo caso, la formula per calcolare la statistica del test di ipotesi per la varianza di due popolazioni è:

$F=\cfrac{s_1^2}{s_2^2}$

Oro:

$F$

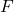
è la statistica di verifica delle ipotesi per la varianza di due popolazioni, che segue una distribuzione F .
$\sigma_1^2$

è la varianza della popolazione 1.
$\sigma_2^2$

è la varianza della popolazione 2.
$s_1^2$

è la varianza del campione 1.
$s_2^2$

è la varianza del campione 2.
$n_1$

è la dimensione del campione 1.
$n_2$

è la dimensione del campione 2.

Poiché la distribuzione Snedecor F non è simmetrica, l’ipotesi nulla viene rifiutata in base ai seguenti criteri:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{nero} \ \text{Se }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più