Come eseguire il test t di welch in r

Il test t di Welch viene utilizzato per confrontare le medie tra due gruppi indipendenti quando non si presume che i due gruppi abbiano varianze uguali.

Per eseguire il t-test di Welch in R, possiamo utilizzare la funzione t.test() , che utilizza la seguente sintassi:

t.test(x, y, alternativa = c(“due facce”, “meno”, “maggiore”))

Oro:

• x: un vettore numerico di valori di dati per il primo gruppo
• y: un vettore numerico di valori di dati per il secondo gruppo
• alternativa: l’ipotesi alternativa per il test. L’impostazione predefinita è fronte-retro.

L’esempio seguente mostra come utilizzare questa funzione per eseguire il test t di Welch in R.

Esempio: test t di Welch in R

Un insegnante desidera confrontare i risultati dell’esame di 12 studenti che hanno utilizzato un libretto di preparazione al test per prepararsi a un esame rispetto a 12 studenti che non lo hanno fatto.

I seguenti vettori mostrano i risultati degli esami degli studenti in ciascun gruppo:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Prima di eseguire il test t di Welch, possiamo creare dei boxplot per visualizzare la distribuzione dei punteggi per ciascun gruppo:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

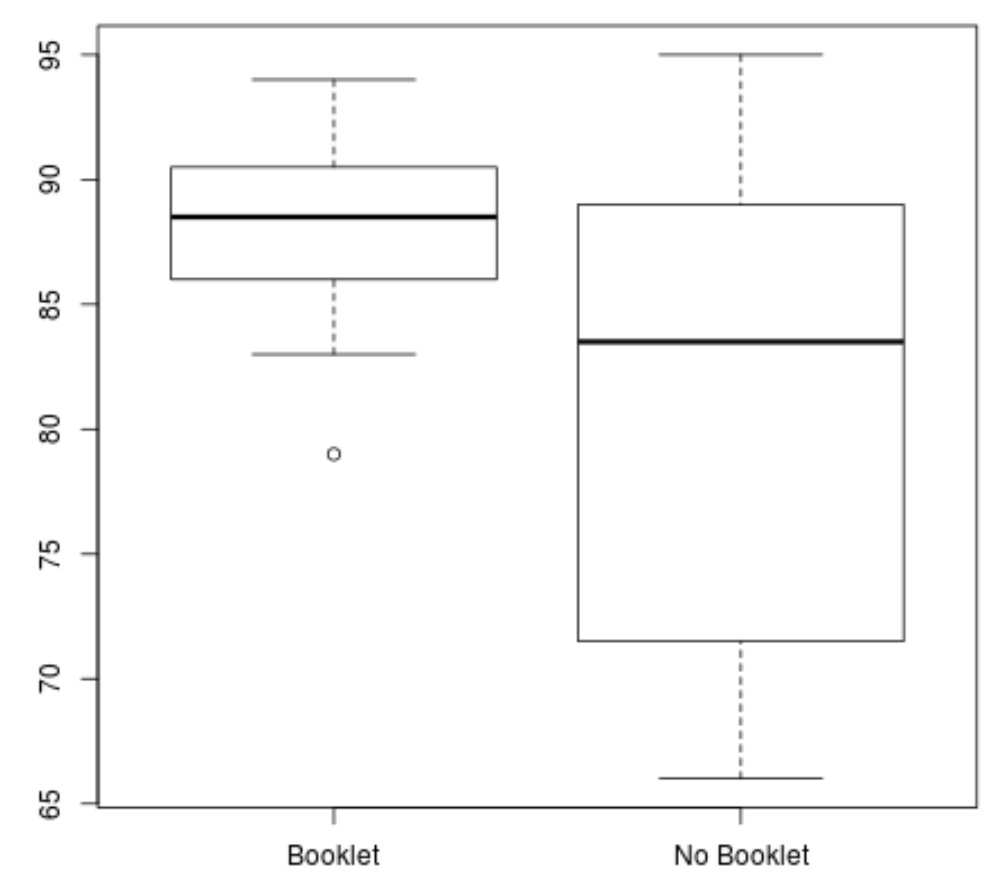
Possiamo vedere chiaramente che il gruppo “Libretto” ha un punteggio medio più alto e una varianza del punteggio più bassa.

Per verificare formalmente se i punteggi medi tra i gruppi sono significativamente diversi, possiamo eseguire il test t di Welch:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

Dal risultato, possiamo vedere che la statistica t -test è 2,2361 e il corrispondente valore p è 0,04171 .

Poiché questo valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla e concludere che esiste una differenza statisticamente significativa nei punteggi medi degli esami tra i due gruppi.

La funzione t.test() ci fornisce anche le seguenti informazioni:

• L’ intervallo di confidenza al 95% per la differenza nei punteggi medi degli esami tra i due gruppi è [0,3048, 13,8618 ].
• Il punteggio medio degli esami del primo gruppo è 87,91667 .
• Il punteggio medio dell’esame del secondo gruppo è 80,83333 .

Puoi trovare la documentazione completa per la funzione t.test() qui .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come eseguire un test t per un campione in R
Come eseguire un t-test a due campioni in R
Come eseguire un t-test per campioni accoppiati in R
Come tracciare più boxplot in un singolo grafico in R