Come eseguire il test t di welch in excel

Il modo più comune per confrontare le medie tra due gruppi indipendenti è utilizzare un test t a due campioni . Tuttavia, questo test presuppone che le varianze tra i due gruppi siano uguali.

Se ritieni che la varianza tra i due gruppi non sia uguale, puoi utilizzare il test t di Welch , che è l’equivalente non parametrico del test t a due campioni.

Questo tutorial spiega come eseguire il test t di Welch in Excel.

Esempio: test t di Welch in Excel

Per questo esempio, confronteremo i risultati di 12 studenti che hanno utilizzato un libretto di preparazione all’esame per prepararsi all’esame rispetto a 12 studenti che non lo hanno fatto.

Utilizzare i passaggi seguenti per eseguire un test t di Welch’t per determinare se esiste una differenza nei punteggi medi degli esami tra i due gruppi.

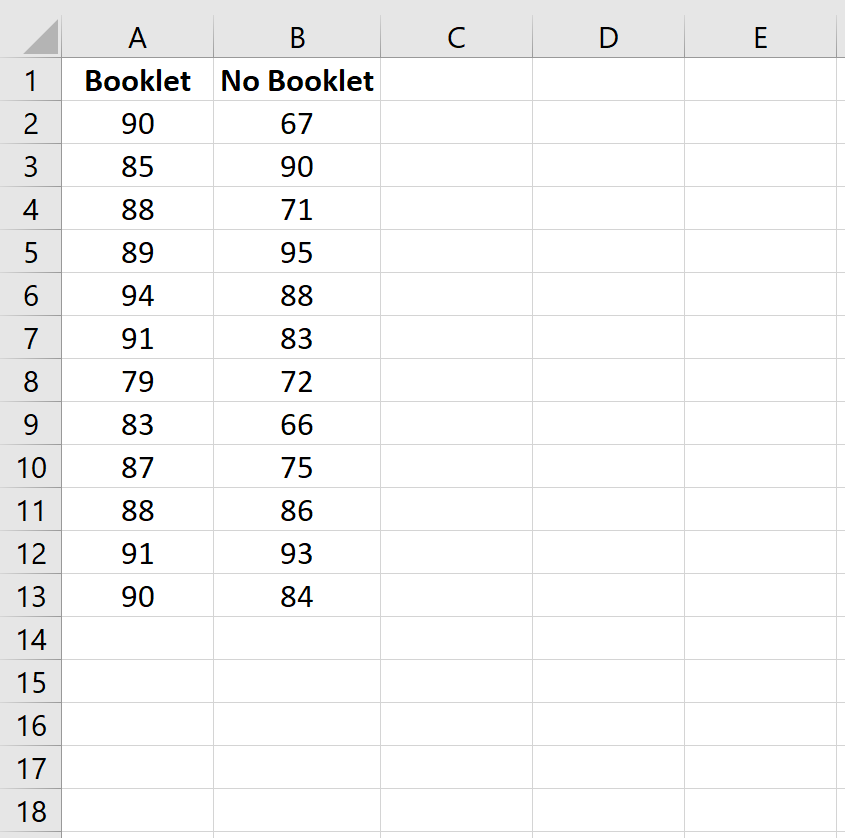
Passaggio 1: inserisci i dati.

Innanzitutto, inserisci i risultati dell’esame in due colonne:

Passaggio 2: eseguire il test t di Welch.

Sulla barra multifunzione superiore di Excel, vai alla scheda Dati e fai clic su Analisi dati . Se non vedi questa opzione, devi prima installare il software gratuito Analysis ToolPak .

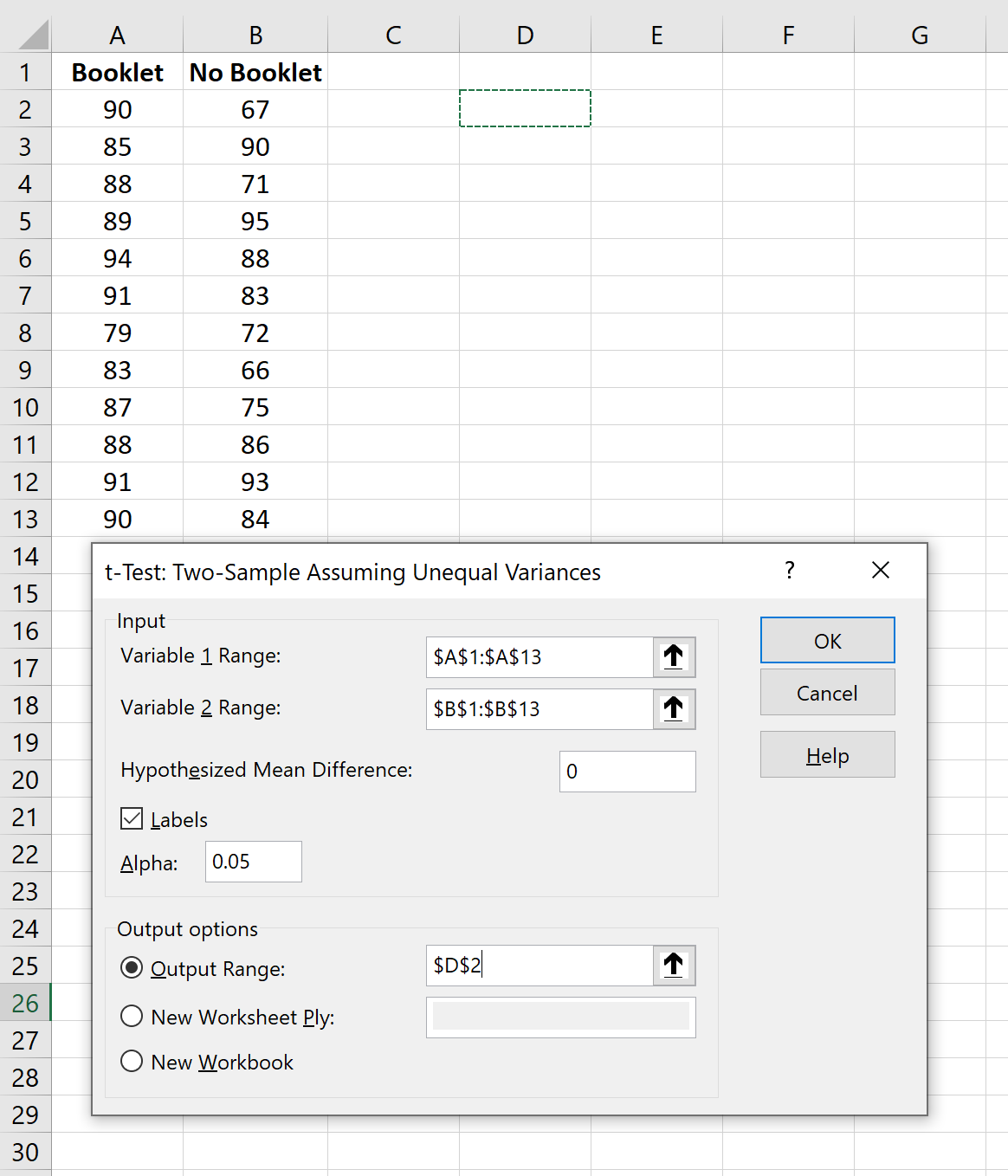
Dopo aver fatto clic su Analisi dati, verrà visualizzata una nuova finestra. Selezionare test t: due campioni assumendo varianze disuguali e fare clic su OK .

Nella nuova finestra, inserisci l’intervallo di valori dei dati per Variabile 1 e Variabile 2 , comprese le etichette dei gruppi. Per Differenza media ipotetica , digitare 0. Selezionare la casella accanto a Etichette . Lasciare Alpha impostato su 0,05. Per Intervallo di output , scegli una cella in cui desideri che vengano visualizzati i risultati del test. Quindi fare clic su OK .

Viene visualizzato automaticamente il seguente output:

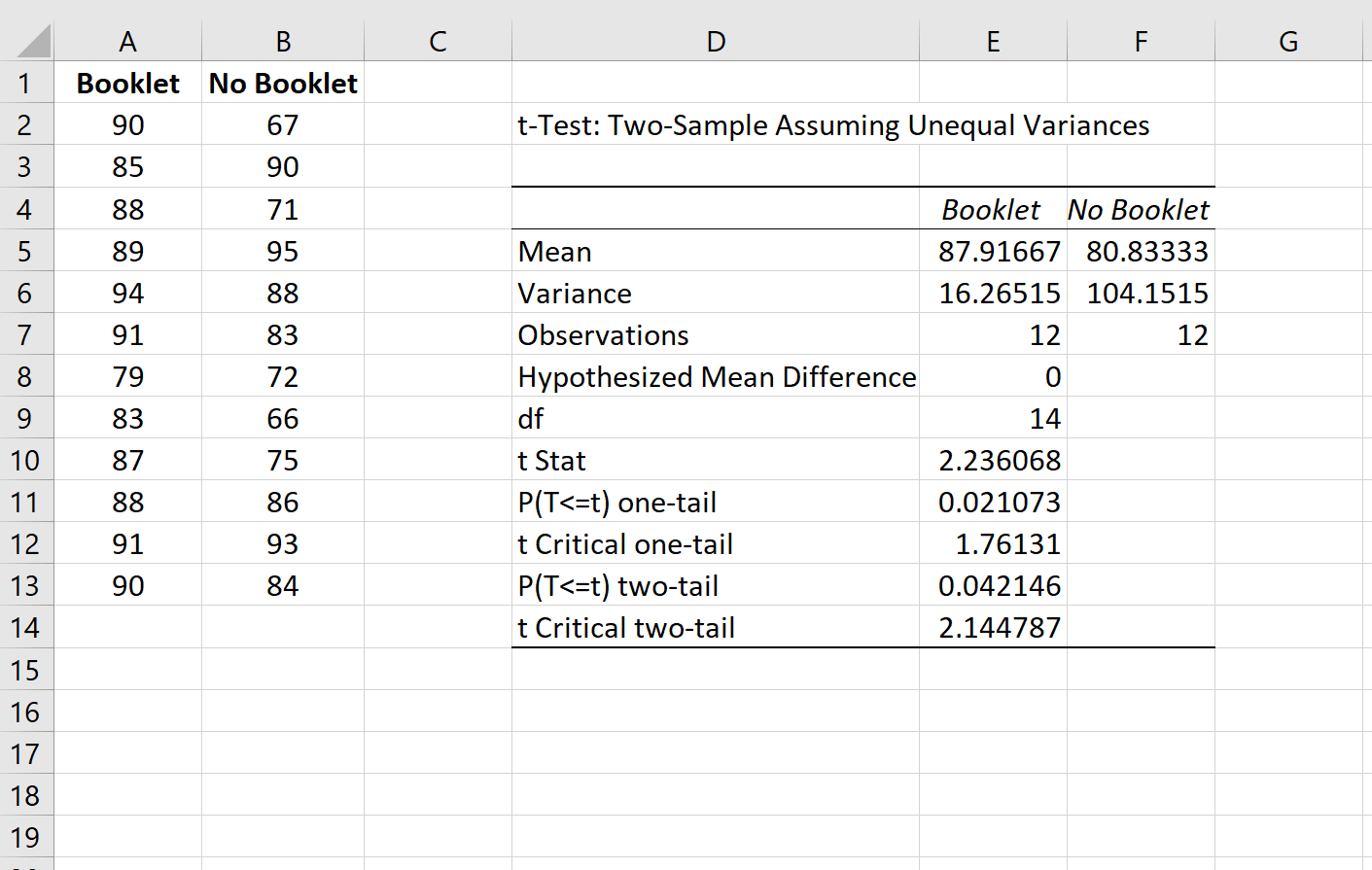
Ecco come interpretare il risultato:

• Media: il punteggio medio dell’esame per ciascun gruppo.
• Varianza: la varianza dei punteggi degli esami per ciascun gruppo.
• Osservazioni: la dimensione del campione per ciascun gruppo.
• Differenza media ipotetica: differenza media da utilizzare nell’ipotesi nulla del test.
• df: i gradi di libertà da utilizzare con la statistica del test, calcolati come n ₁ + n ₂ – 2.
• t Stat: la statistica del test.
• P(T<=t) a una coda: il valore p associato alla statistica del test per un test a una coda. Ignoralo poiché stiamo eseguendo un test a due code.
• P(T<=t) a due code: valore p associato alla statistica del test per un test a due code. Poiché questo è inferiore a 0,05, rifiuteremo l’ipotesi nulla e concluderemo che il punteggio medio dell’esame tra i due gruppi è statisticamente significativo al livello α = 0,05.

Passaggio 3: riportare i risultati.

Infine, vorremmo riportare i risultati del nostro test t di Welch. Ecco un esempio di come eseguire questa operazione:

È stato condotto un test t di Welch per determinare se esistesse una differenza statisticamente significativa nei punteggi degli esami tra un gruppo di studenti che hanno utilizzato un libretto di preparazione all’esame per prepararsi all’esame e un gruppo che non lo ha utilizzato. La dimensione del campione per entrambi i gruppi era di 12 studenti.

Il t-test di Welch ha rivelato che c’era una differenza statisticamente significativa nei punteggi medi degli esami (t=2,236, p=0,0421) tra i due gruppi.