Come calcolare i punteggi z in sas

Nelle statistiche, un punteggio z ci dice quante deviazioni standard un valore è dalla media .

Usiamo la seguente formula per calcolare uno z-score:

z = (X – μ) / σ

Oro:

• X è un singolo valore di dati grezzi
• μ è la media del set di dati
• σ è la deviazione standard del set di dati

L’esempio seguente mostra come calcolare i punteggi z per i valori dei dati grezzi in SAS.

Esempio: calcolare i punteggi Z in SAS

Supponiamo di creare il seguente set di dati in SAS:

 /*create dataset*/
data original_data;
    input values;
    datalines ;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run ;

/*view dataset*/
proc print data = original_data;

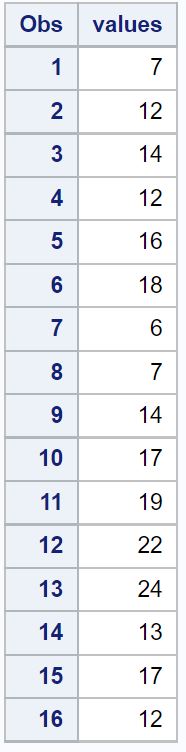
Supponiamo ora di voler calcolare il punteggio z per ciascun valore nel set di dati.

Possiamo usare proc sql per fare questo:

 /*create new variable that shows z-scores for each raw data value*/
proc sql ;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit ; 

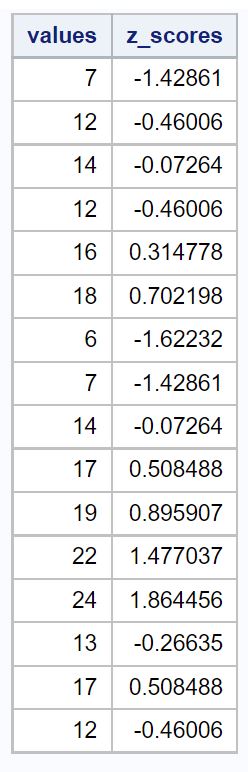
La colonna dei valori mostra i valori dei dati originali e la colonna z_scores mostra il punteggio z per ciascun valore.

Come interpretare i punteggi Z in SAS

Un punteggio z ci dice quante deviazioni standard un valore è dalla media.

Un punteggio z può essere positivo, negativo o zero.

Un punteggio z positivo indica che un valore particolare è superiore alla media, un punteggio z negativo indica che un valore particolare è inferiore alla media e un punteggio z pari a zero indica che un valore particolare è uguale alla media.

Se calcolassimo la media e la deviazione standard del nostro set di dati, troveremmo che la media è 14.375 e la deviazione standard è 5.162 .

Quindi il primo valore nel nostro set di dati era 7, che aveva un punteggio z di (7-14.375) / 5.162 = -1.428 . Ciò significa che il valore “7” è 1.428 deviazioni standard inferiori alla media.

Il valore successivo nei nostri dati, 12, aveva un punteggio z di (12-14,375) / 5,162 = -0,46 . Ciò significa che il valore “12” è 0,46 deviazioni standard inferiori alla media.

Quanto più un valore è lontano dalla media, tanto più alto sarà il valore assoluto del punteggio z per quel valore.

Ad esempio, il valore 7 è più lontano dalla media (14,375) rispetto al valore 12, il che spiega perché 7 aveva un punteggio z con un valore assoluto maggiore.

Risorse addizionali

I seguenti articoli spiegano come eseguire altre attività comuni in SAS:

Come identificare i valori anomali in SAS
Come calcolare i percentili in SAS
Come calcolare media, mediana e moda in SAS