Come calcolare i punteggi z in spss

Un punteggio z ci dice quante deviazioni standard un dato valore è dalla media.

Il punteggio z di un dato valore viene calcolato come segue:

Punteggio z = (x – μ) / σ

Oro:

• x: valore individuale
• μ: media della popolazione
• σ: deviazione standard della popolazione

Questo tutorial spiega come calcolare i punteggi z in SPSS.

Correlato: Come interpretare i punteggi Z

Come calcolare i punteggi Z in SPSS

Supponiamo di avere il seguente set di dati che mostra il reddito annuo (in migliaia) di 15 persone:

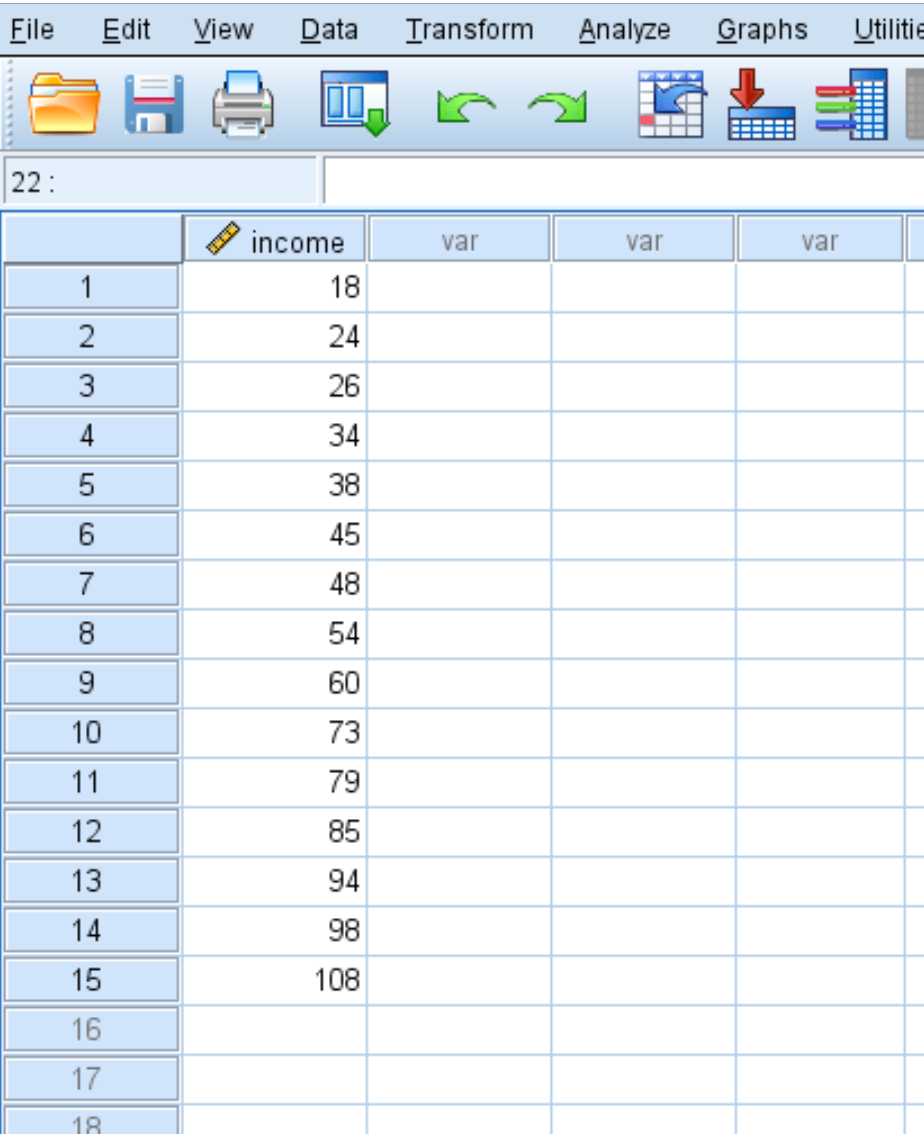
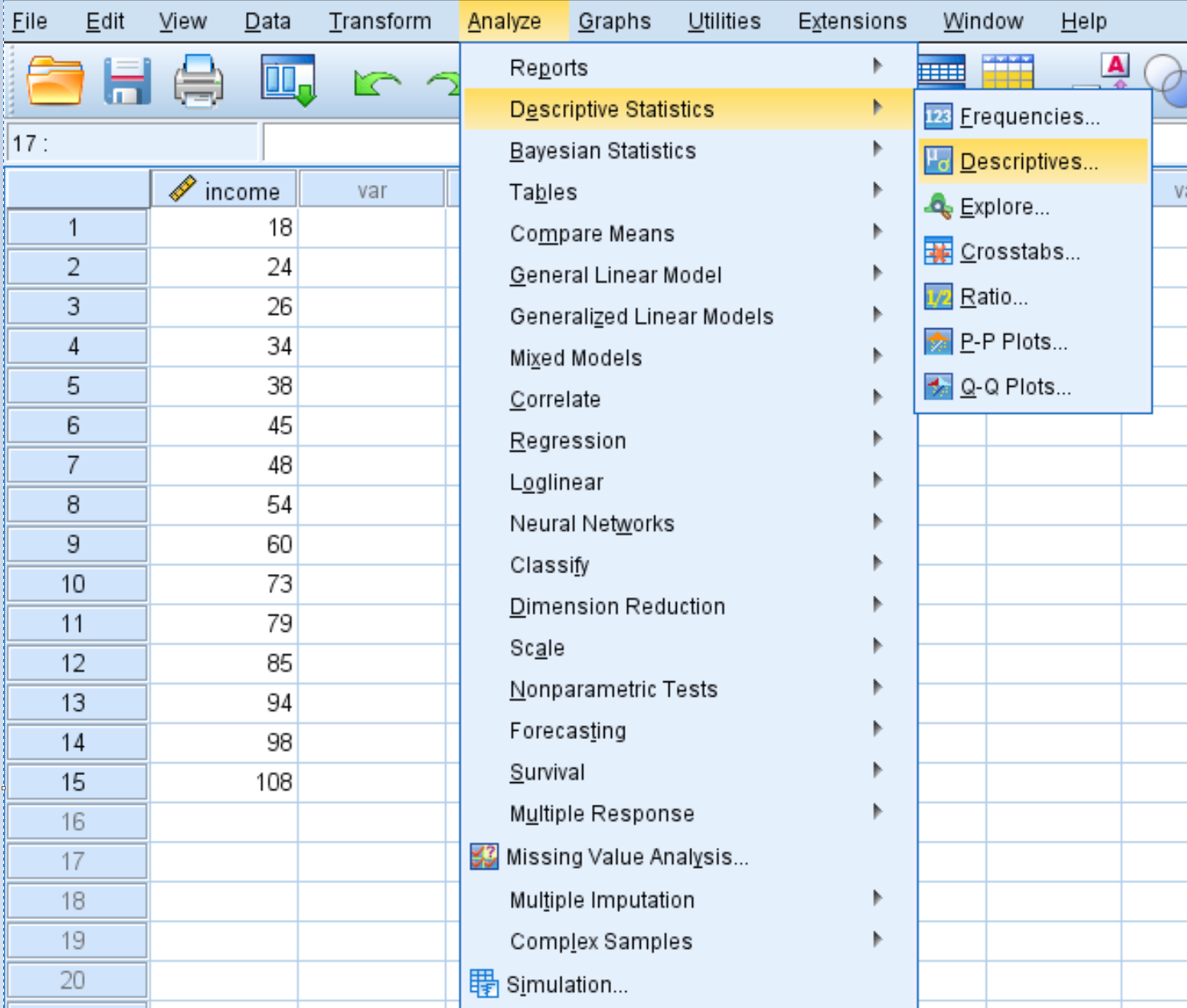
Per calcolare i punteggi z per ciascun valore nel set di dati, fare clic sulla scheda Analizza , quindi su Statistiche descrittive e quindi su Descrittive :

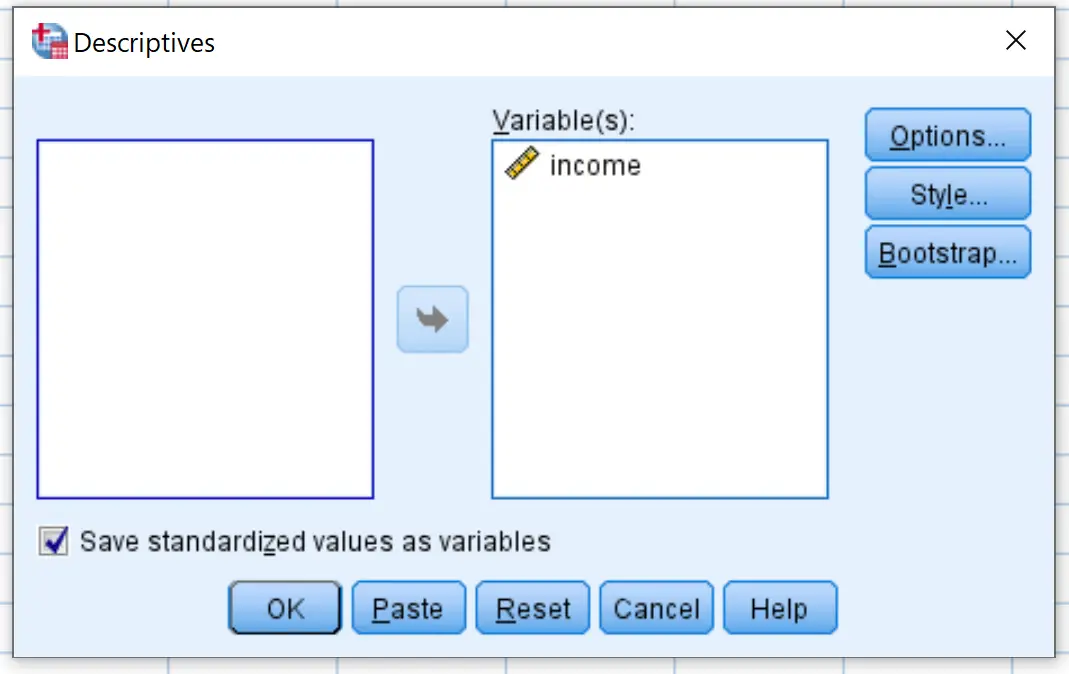
Nella nuova finestra che appare, trascina la variabile reddito nella casella denominata Variabile/i.

Assicurati che la casella accanto a Salva valori standardizzati come variabili sia selezionata, quindi fai clic su OK .

Dopo aver fatto clic su OK , SPSS produrrà una tabella di statistiche descrittive per il set di dati:

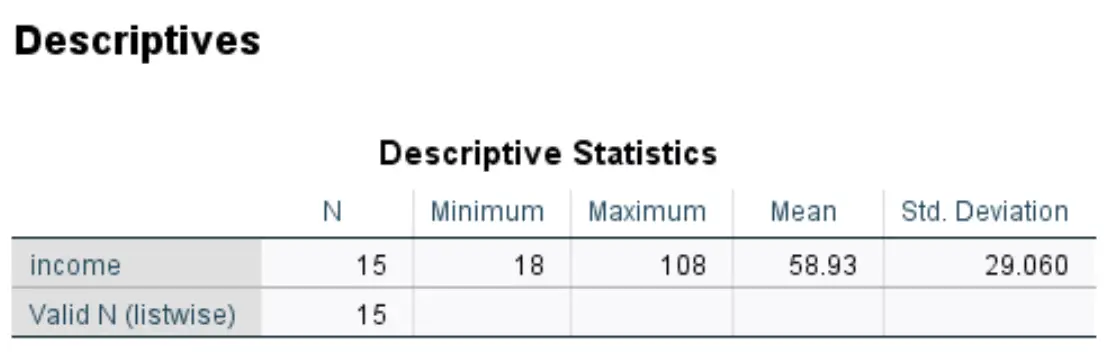
SPSS produrrà anche una nuova colonna di valori che visualizza il punteggio z per ciascuno dei valori originali nel set di dati:

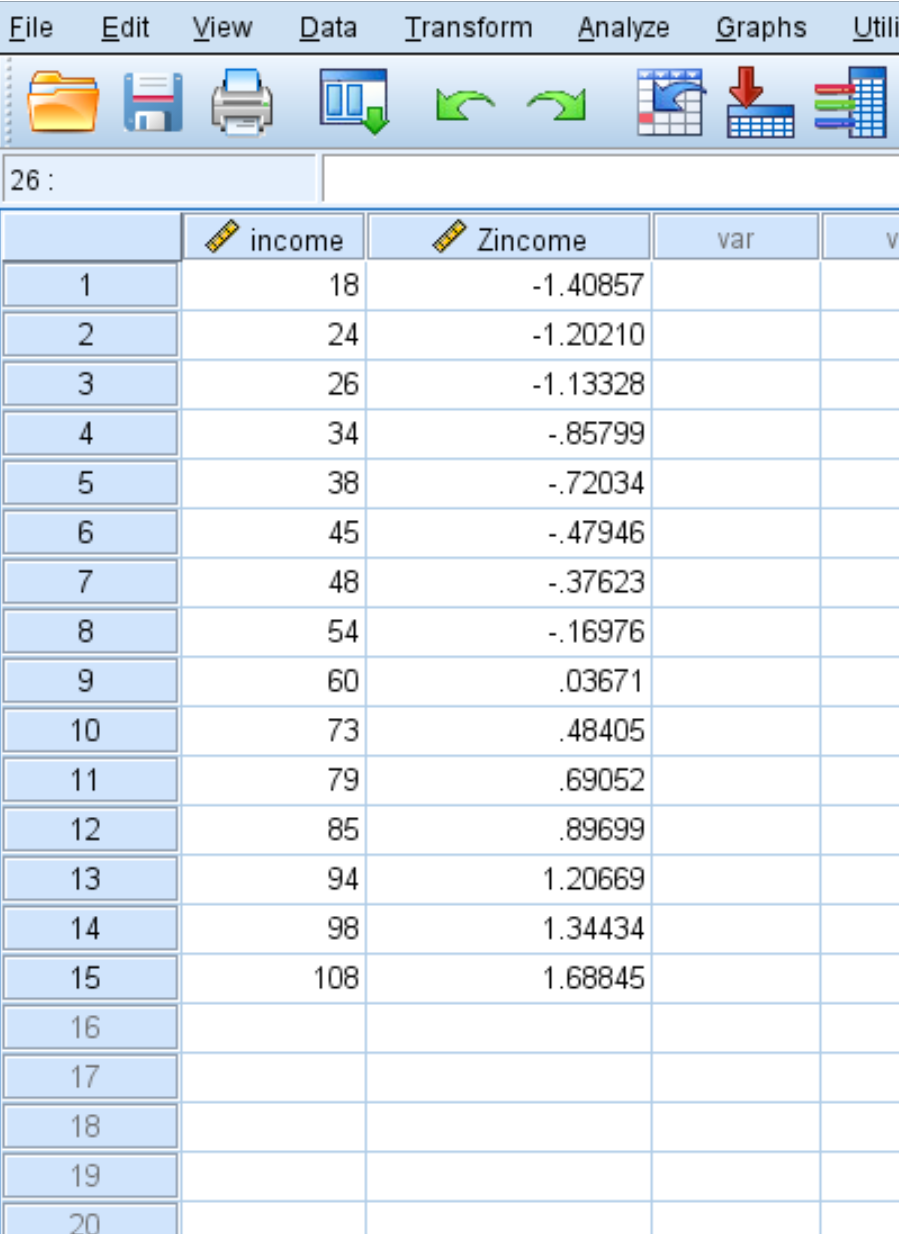
Ciascuno dei punteggi z viene calcolato utilizzando la formula z = (x – μ) / σ

Ad esempio, il punteggio z per il valore del reddito pari a 18 è:

z = (18 – 58,93) / 29,060 = -1,40857 .

I punteggi Z per tutti gli altri valori dei dati vengono calcolati allo stesso modo.

Come interpretare i punteggi Z

Ricorda che un punteggio z ci dice semplicemente quante deviazioni standard un valore è dalla media.

Un punteggio z può essere positivo, negativo o uguale a zero:

• Un punteggio z positivo indica che un particolare valore è superiore alla media.
• Un punteggio z negativo indica che un particolare valore è inferiore alla media.
• Un punteggio z pari a zero indica che un particolare valore è uguale alla media.

Nel nostro esempio, abbiamo scoperto che la media era 58,93 e la deviazione standard era 29,060.

Pertanto, il primo valore nel nostro set di dati era 18, che aveva un punteggio z di (18 – 58,93) / 29,060 = -1,40857 .

Ciò significa che il valore “18” è 1.40857 deviazioni standard inferiori alla media.

Al contrario, l’ultimo valore nei nostri dati era 108, che corrispondeva a un punteggio z di (108 – 58,93) / 29,060 = 1,68845 .

Ciò significa che il valore “108” è 1,68845 deviazioni standard sopra la media.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SPSS:

Come calcolare le statistiche descrittive per le variabili in SPSS
Come calcolare un riepilogo a cinque cifre in SPSS
Come identificare i valori anomali in SPSS