なぜ統計が重要なのでしょうか? (統計が重要である 10 の理由!)

統計の分野は、データの収集、分析、解釈、表示に関係します。

テクノロジーが私たちの日常生活にますます浸透するにつれて、人類史上かつてないほど多くのデータが生成および収集されています。

統計は、このデータを使用して次のタスクを実行する方法を理解するのに役立つ領域です。

• 私たちの周りの世界をよりよく理解します。
• データを使用して意思決定を行います。
• データを使用して未来を予測します。

この記事では、統計分野が現代生活において非常に重要である10の理由を紹介します。

理由 1: 記述統計を使用して世界を理解する

記述統計は、生データを説明するために使用されます。記述統計には主に 3 つのタイプがあります。

• 概要統計
• グラフィックス
• テーブル

これらの各要素は、既存のデータをより深く理解するのに役立ちます。

たとえば、ある都市の 10,000 人の学生のテストのスコアを示す生データ セットがあるとします。記述統計は次の目的で使用される場合があります。

• テストの平均点とテスト結果の標準偏差を計算します。
• ヒストグラムまたは箱ひげ図を生成して、テスト結果の分布を視覚化します。
• 頻度表を作成して、テスト結果の分布を理解します。

記述統計を使用すると、生データを見るだけよりもはるかに簡単に生徒のテストの得点を理解できます。

理由 2: 誤解を招くグラフィックに注意してください

ジャーナル、メディア、オンライン記事、雑誌では、ますます多くのグラフィックが作成されています。残念ながら、基礎となるデータを理解していないと、グラフは誤解を招く可能性があります。

たとえば、ある大学の学生の GPA スコアと ACT スコアの間に負の相関があることを発見した研究結果が雑誌に掲載されたとします。

ただし、この負の相関関係は、GPA と ACT スコアの両方が高い学生はエリート大学に進学できるのに対し、GPA と ACT スコアの両方が低い学生はまったく入学できないためにのみ発生します。

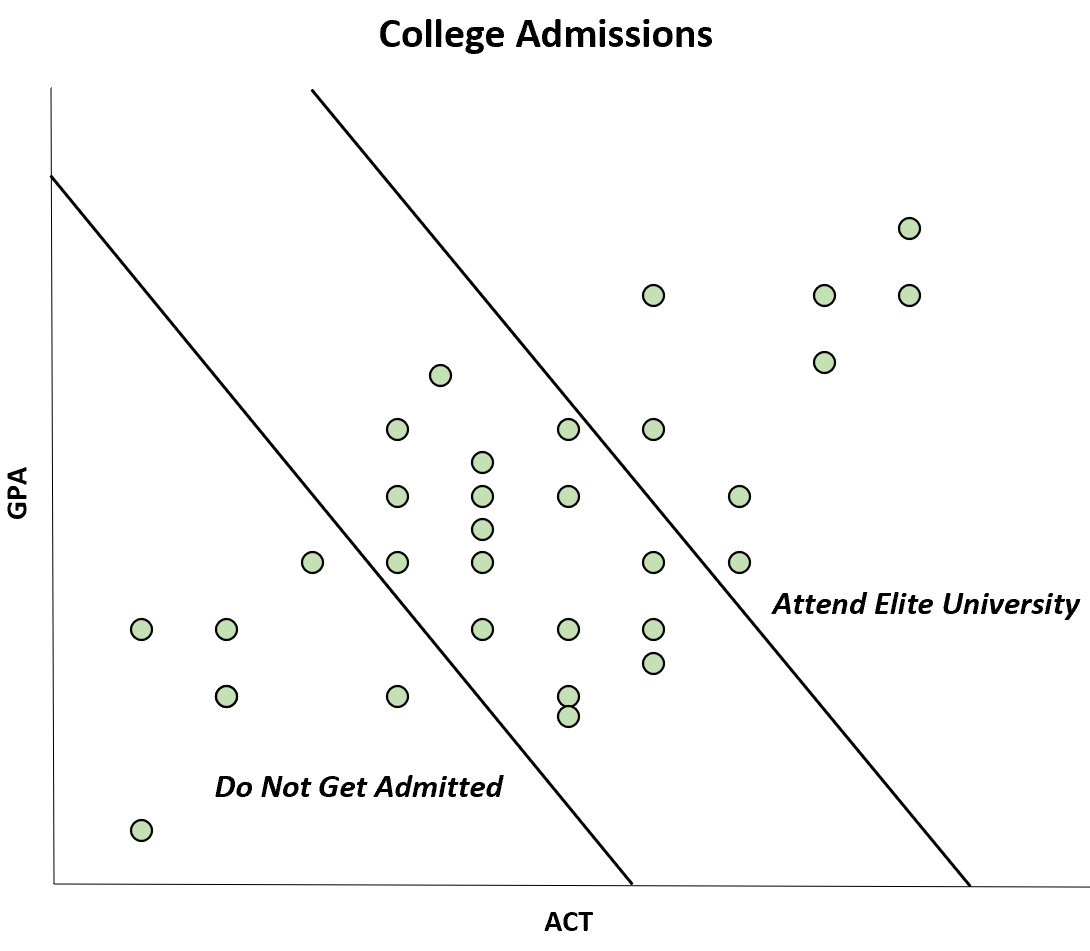
ACT と GPA の相関関係は母集団では正ですが、サンプルでは負の相関が見られます。

この特定のバイアスは、 バークソン バイアスとして知られています。このバイアスを意識することで、特定のチャートに惑わされないようにすることができます。

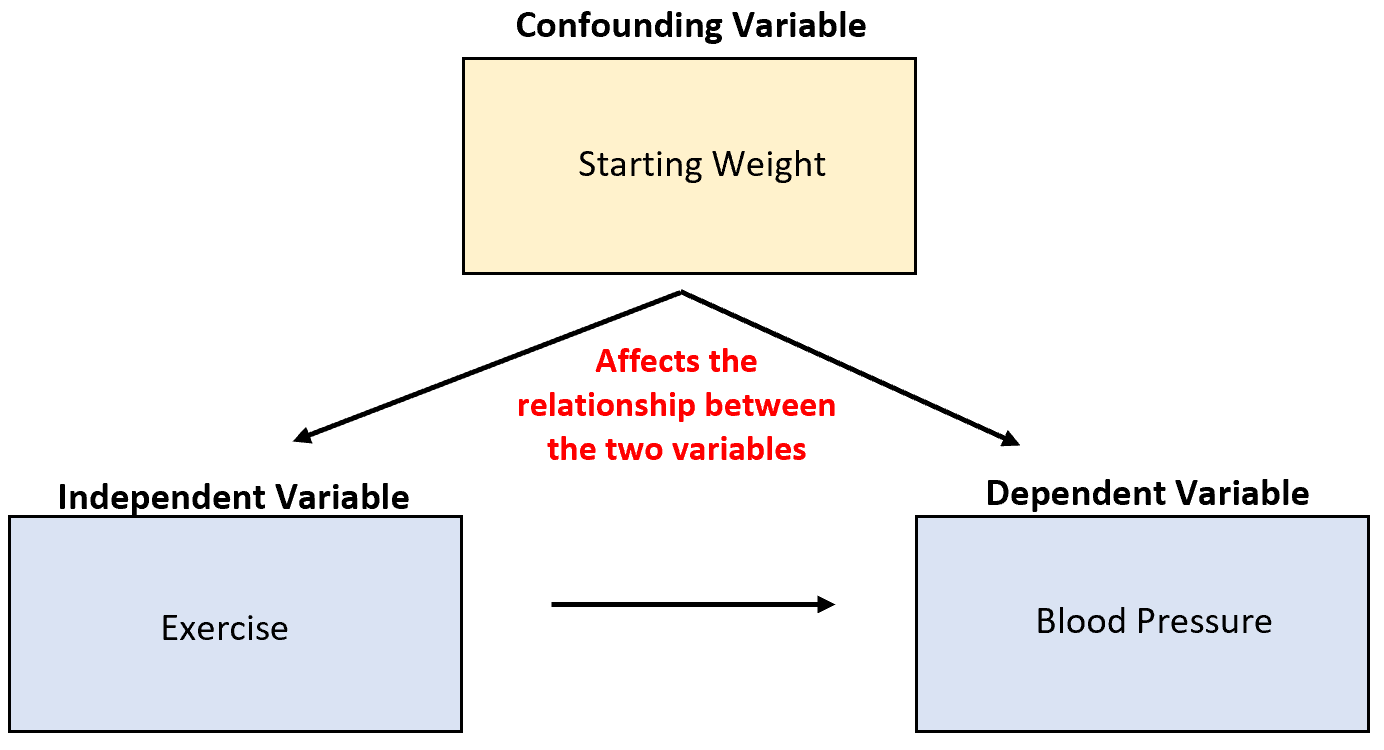
理由 3: 紛らわしい変数に注意する

統計で学ぶ重要な概念は、混乱を招く変数の概念です。

これらは考慮されていない変数であり、実験の結果を混乱させ、信頼性の低い結論につながる可能性があります。

たとえば、研究者がアイスクリームの販売とサメの襲撃に関するデータを収集し、2 つの変数に高い相関があることを発見したとします。これは、アイスクリームの売上の増加がサメの襲撃を引き起こしていることを意味するのでしょうか?

それはありそうにありません。最も考えられる原因は、紛らわしい温度変数です。外が暖かくなると、アイスクリームを買う人も海に行く人も増えます。

理由 4: 確率を使用してより適切な意思決定を行うため

統計の最も重要なサブフィールドの 1 つは確率です。事象が起こる確率を研究する分野です。

確率の基本を理解することで、現実の世界でより多くの情報に基づいた意思決定を行うことができます。

たとえば、ある高校生が、特定の大学に合格する可能性が 10% であることを知っているとします。この学生は、 「少なくとも 1 つ」の合格確率の公式を使用して、出願する少なくとも 1 つの大学に合格する確率を求め、結果に応じて出願する大学の数を調整できます。

理由 5: 研究における P 値を理解する

統計で学ぶもう 1 つの重要な概念はp 値です。

p 値の古典的な定義は次のとおりです。

p 値は、帰無仮説が真であると仮定した場合に、標本統計量と少なくとも同じくらい極端な標本統計量が観察される確率です。

たとえば、ある工場が平均重量 200 ポンドのタイヤを生産していると主張しているとします。監査人は、この工場で生産されるタイヤの実際の平均重量は 200 ポンド異なると仮説を立てています。そこで、仮説検定を実行したところ、検定の p 値が 0.04 であることがわかりました。

この p 値を解釈する方法は次のとおりです。

工場が実際に平均重量 200 ポンドのタイヤを製造している場合、ランダムなサンプリング誤差により、すべての監査の 4% がサンプルで観察された効果以上に達します。これは、工場が実際に平均重量 200 ポンドのタイヤを製造している場合、監査人が取得したサンプル データを入手することは非常にまれであることを示しています。

したがって、監査人は、この工場で生産されるタイヤの実際の平均重量が確かに 200 ポンドであるという帰無仮説を棄却する可能性があります。

理由 6: 相関関係を理解する

統計学で学ぶもう 1 つの重要な概念は、2 つの変数間の線形関連性を示す相関 関係です。

相関係数の値は常に -1 と 1 の間になります。ここで、

• -1 は、2 つの変数間の完全な負の線形相関を示します。
• 0 は 2 つの変数間に線形相関がないことを示します
• 1 は、2 つの変数間の完全な正の線形相関を示します。

これらの値を理解することで、現実世界の変数間の関係を理解することができます。

たとえば、広告支出と収益の相関関係が 0.87 の場合、2 つの変数間に強い正の関係があることがわかります。広告に費やすお金が増えるほど、予想通りの収益増加が期待できます。

理由 7: 未来について予測する

統計を学ぶもう 1 つの重要な理由は、次のような基本的な回帰モデルを理解することです。

• 単純な線形回帰
• 多重線形回帰
• ロジスティック回帰

これらの各モデルを使用すると、モデル内の特定の予測変数の値に基づいて、応答変数の将来の値を予測できます。

たとえば、企業は現実世界において、年齢、収入、民族などの予測変数を使用する場合、常に多重線形回帰モデルを使用します。店舗で何人の顧客が買い物をするかを予測します。

同様に、物流会社は総需要、人口規模などの予測変数を使用します。将来の売上を予測するため。

どのような分野で働いているとしても、将来の現象を予測するために回帰モデルが使用される可能性は十分にあります。

理由 8: 研究における潜在的なバイアスを理解する

統計を研究するもう 1 つの理由は、現実の研究で発生する可能性のあるさまざまな種類のバイアスをすべて認識することです。

ここではいくつかの例を示します。

• バイアスを観察する
• 自己選択バイアス
• 基準バイアス
• 省略された変数バイアス
• アンダーカウントバイアス
• 無回答バイアス

このようなタイプのバイアスについて基本的に理解しておくと、研究を行うときにバイアスを回避したり、他の研究論文や研究を読むときにバイアスに注意したりすることができます。

理由 9: 統計検定によって作成された仮定を理解する

多くの統計テストでは、調査対象の基礎となるデータについての仮定が行われます。

研究結果を読むとき、あるいは自分で研究を行うときでも、結果が信頼できるものであるためにはどのような仮定を置く必要があるかを理解することが重要です。

以下の記事では、一般的に使用される多くの統計テストや手順で行われる仮定を共有します。

• 統計における等分散仮定とは何ですか?
• 統計における正規性の仮定とは何ですか?
• 統計における独立性の仮定とは何ですか?

理由 10: 過度の一般化を避けるため

統計を勉強するもう 1 つの理由は、過剰一般化の概念を理解することです。

これは、研究に参加している個人が集団全体の個人を代表しておらず、したがって研究の結果を集団全体に一般化することが不適切な場合に発生します。

たとえば、ある学校の生徒の何パーセントが好きな映画のジャンルとして「ドラマ」を好むかを知りたいとします。生徒の総人口が男子 50%、女子 50% の混合である場合、好きなジャンルとして演劇を好む男子生徒が大幅に少ない場合、男子 90%、女子 10% からなるサンプルでは偏った結果が生じる可能性があります。

理想的には、サンプルは母集団の「ミニバージョン」に似ていることが望ましいです。したがって、学生人口全体が女子 50%、男子 50% で構成されている場合、90% の男子と 10% の女子だけが含まれている場合、サンプルは代表的ではありません。

したがって、独自の調査を実施する場合でも、調査結果を読む場合でも、サンプル データが母集団全体を代表しているかどうか、また調査結果が自信を持って母集団に一般化できるかどうかを理解することが重要です。

追加リソース

統計入門における最も重要な概念の基本を理解するには、次の記事を参照してください。

記述統計または推論統計
人口 vs.サンプル
統計とパラメータ
質的変数と量的変数
測定レベル: 名目、順序、間隔、比率