Sas で二元配置分散分析を実行する方法

二元配置分散分析は、 2 つの変数 (「因子」と呼ばれることもあります) に割り当てられた 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

このチュートリアルでは、SAS で二元配置分散分析を実行する方法の例を段階的に説明します。

ステップ 1: データを作成する

植物学者が、日光への曝露や水やりの頻度が植物の成長に影響を与えるかどうかを知りたいとします。

彼女は 30 個の種を植え、日光への曝露や水やりの頻度などのさまざまな条件で 1 か月間成長させます。 1 か月後、彼女は各植物の高さを記録します。結果を以下に示します。

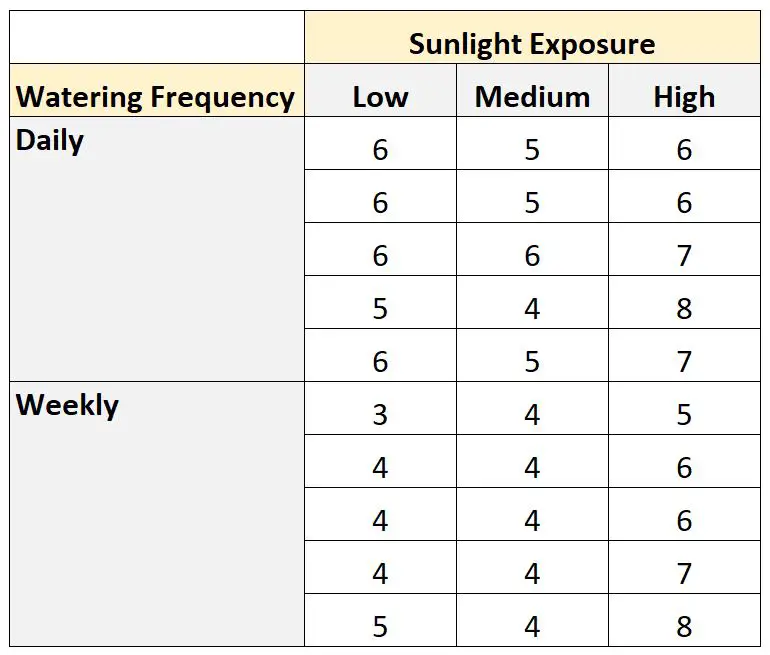
次のコードを使用して、SAS でこのデータセットを作成できます。

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

ステップ 2: 二元配置分散分析を実行する

次に、 proc ANOVA を使用して二元配置分散分析を実行します。

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

ステップ 3: 結果を解釈する

結果で分析する最初のテーブルは ANOVA テーブルです。

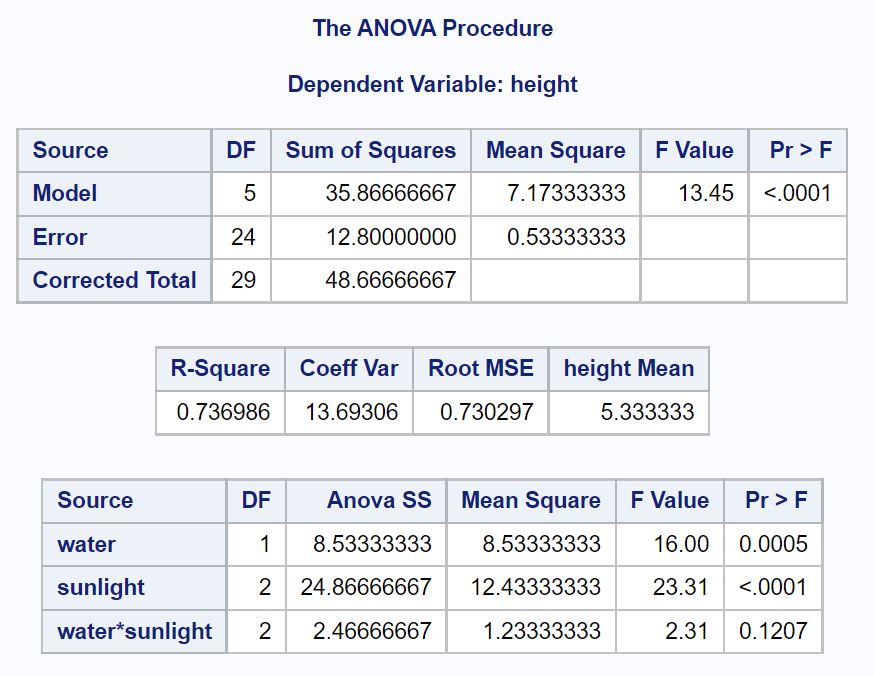
この表から次のことがわかります。

• 水の p 値: 0.0005
• 太陽光の p 値: <.0001
• 水と太陽光の間の相互作用の p 値: 。 1207

これは、水と太陽光が統計的に有意な植物の高さの予測因子であり、水と太陽光の間には統計的に有意な相互作用効果がないことがわかります。

次に、Tukey の事後テストの結果を調べて、どの水と太陽光のレベルが統計的に有意に異なるかを判断できます。

まず、Tukey による水の事後比較を見てみましょう。

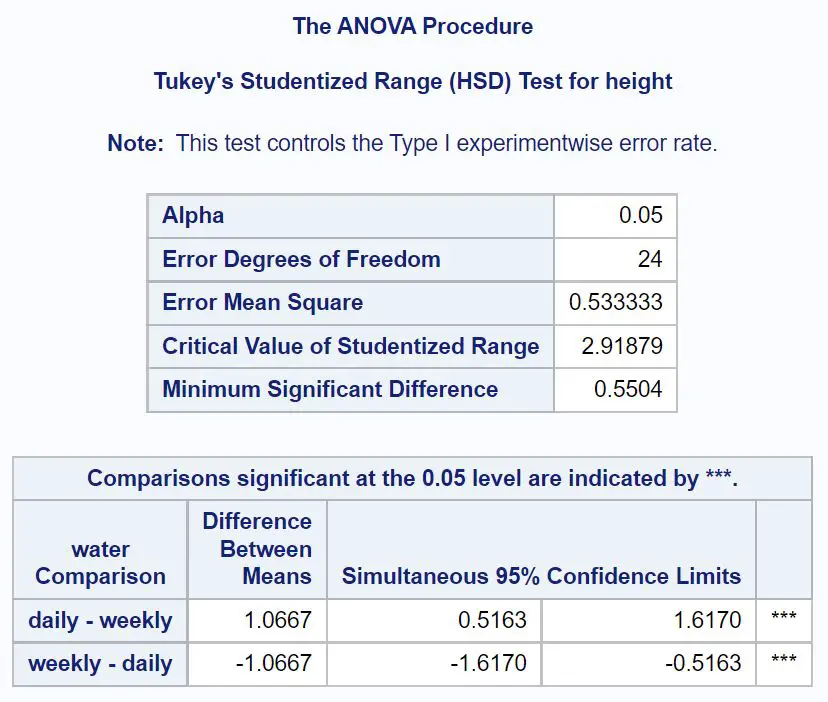
結果から、毎日水を与えた植物と毎週水を与えた植物の高さの平均差は1.0667インチであることがわかります。

平均サイズの差の 95% 信頼区間は[.5163, 1.6170]です。これは、毎日水を与えた植物と毎週水を与えた植物の平均高さの実際の差が 0.5163 インチから 1.6170 インチの間であることを 95% 確信していることを意味します。

まず、太陽光に関する Tukey の事後比較を見てみましょう。

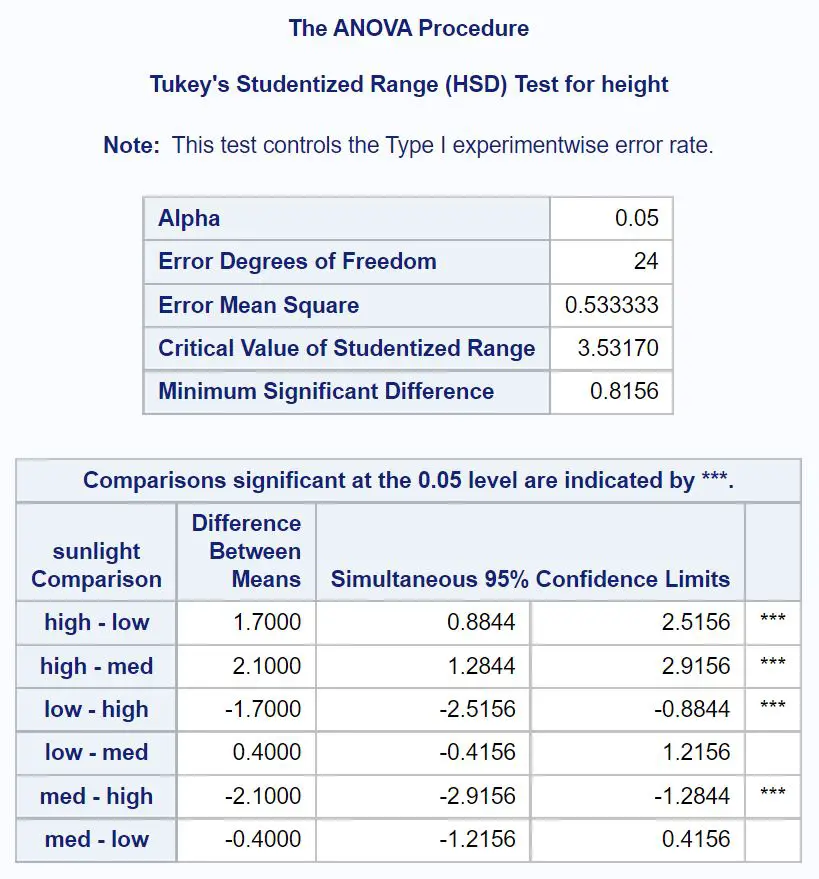
どのグループ平均が異なるかを調べるには、どのペアごとの比較の横に星 ( *** ) が付いているかを確認する必要があります。

表から、次のグループの平均値が統計的に有意に異なることがわかります。

• 日照量が多いか少ないか (95% CI = [.8844, 2.5156])
• 日照量が多いまたは中程度の日照量 (95% CI = [1.2844, 2.9156])

ステップ 4: 結果を報告する

最後に、二元配置分散分析の結果を報告します。

二元配置分散分析を実行して、水やりの頻度と日光への曝露が植物の成長に及ぼす影響を分析しました。

二元配置分散分析により、水やりの頻度と日光曝露の影響の間に統計的に有意な相互作用がないことが明らかになりました (p = 0.1207)。

簡単な手の影響分析により、水やりの頻度が植物の成長に統計的に有意な影響を与えることが示されました (p = 0.0005)。

簡単な手の影響分析では、日光への曝露も植物の成長に統計的に有意な影響を与えることが示されました (p < 0.0001)。

追加リソース

次のチュートリアルでは、二元配置 ANOVA に関する追加情報を提供します。

二元配置分散分析の概要
一元配置分散分析または二元配置分散分析: いつ使用するか?
二元配置分散分析を手動で実行する方法