Sas で 1 サンプルの t 検定を実行する方法
1 サンプルの t 検定は、 母集団の平均が特定の値に等しいかどうかを判断するために使用されます。
このチュートリアルでは、SAS で 1 サンプルの t 検定を実行する方法について説明します。
例: SAS のサンプル t 検定
植物学者が、特定の種類の植物の平均高さが 15 インチに等しいかどうかを知りたいとします。彼女は 12 本の植物から 無作為にサンプルを採取し、それぞれの高さをインチ単位で記録しました。
高さは14、14、16、13、12、17、15、14、15、13、15、14です。
次の手順を使用して 1 サンプルの t 検定を実行し、この植物種の平均高さが実際に 15 インチであるかどうかを判断します。
ステップ 1: データを作成します。
まず、次のコードを使用して SAS にデータセットを作成します。
/*create dataset*/ data my_data; inputHeight ; datalines ; 14 14 16 13 12 17 15 14 15 13 15 14 ; run ; /*print dataset*/ proc print data =my_data;
ステップ 2: 1 サンプルの t 検定を実行します。
次に、 proc ttest を使用して例に対して t 検定を実行します。
/*perform one sample t-test*/ proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ; varHeight ; run ;
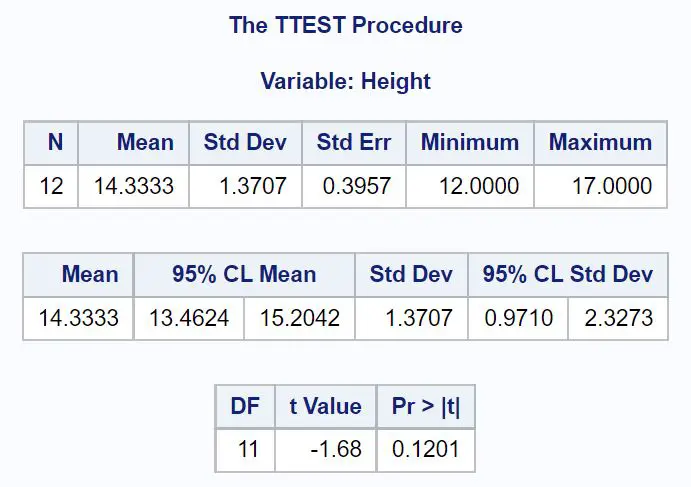
最初の表には、次のようなサンプルの記述統計が表示されます。
- N (観察総数): 12
- 平均 (サンプル平均): 14.3333
- Std Dev (サンプル標準偏差): 1.3707
- 標準誤差 (標準誤差、s/ √nとして計算): 0.3957
- Minimum(最小値): 12
- 最大値(最大値) 17
2 番目の表には、母集団の真の平均値の 95%信頼区間が表示されます。
- μの95% CI: [13.4624, 15.2042]
3 番目の表には、t 検定統計量と対応する p 値が表示されます。
- t 検定統計量: -1.68
- p値: 0.1201
注: 検定統計量は次のように計算されました。
- t 検定統計量 = ( x – μ) / (s/ √n )
- t 検定統計量 = (14.3333-15) / (1.3707/√ 12 )
- t 検定統計量 = -1.68
1 サンプル t 検定では次の帰無仮説と対立仮説が使用されることを思い出してください。
- H 0 : μ = 15 インチ
- H A : μ ≠ 15 インチ
p 値 ( .1201 ) は 0.05 未満ではないため、帰無仮説を棄却できません。
これは、一部の植物種の平均高さが 15 インチよりも異なると言える十分な証拠がないことを意味します。
追加リソース
次のチュートリアルでは、SAS で他の一般的な統計テストを実行する方法について説明します。