オッズ比の解釈方法

統計学において、確率とは、事象が発生する確率を指します。次のように計算されます。

確率：

P(イベント) = (望ましい結果の数) / (考えられる結果の数)

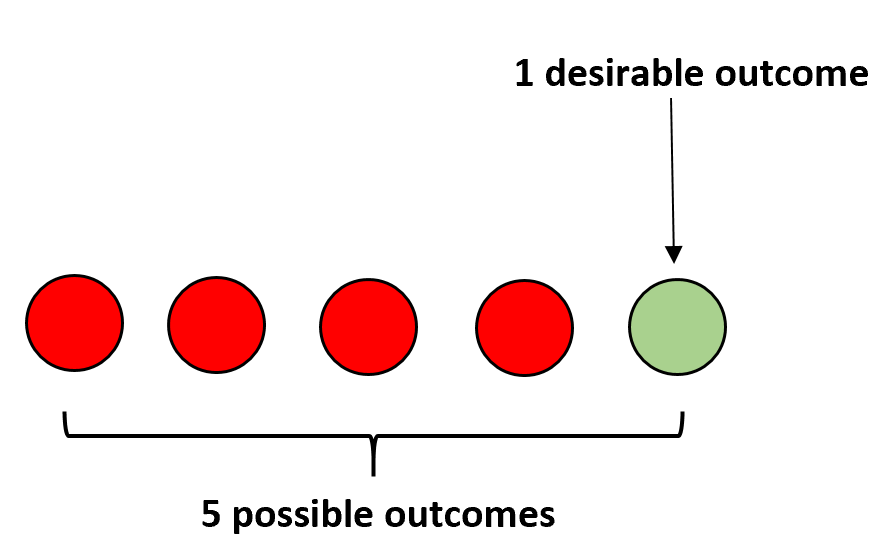
たとえば、袋の中に赤いボールが 4 つと緑のボールが 1 つ入っているとします。目を閉じてボールをランダムに選択した場合、緑色のボールを選択する確率は次のように計算されます。

P(緑) = 1 / 5 = 0.2 。

イベントが発生する確率は次のように計算できます。

オッズ:

チャンス (イベント) = P (イベント発生) / 1-P (イベント発生)

たとえば、緑色のボールが発射される確率は (0.2)/1-(0.2) = 0.2/0.8 = 0.25です。

オッズ比は2 つの確率の比です。

運のレポート:

オッズ比 = イベント A のオッズ / イベント B のオッズ

たとえば、赤いボールを選択する場合と緑のボールを選択する場合のオッズ比を計算できます。

赤いボールを引く確率は 4/5 = 0.8です。

赤いボールを引く確率は (0.8) / 1-(0.8) = 0.8 / 0.2 = 4です。

緑のボールよりも赤のボールを選択するオッズ比は次のように計算されます。

オッズ (赤) / オッズ (緑) = 4 / 0.25 = 16 。

したがって、赤いボールが発射される確率は、緑のボールが発射される確率より 16 倍大きくなります。

オッズ比は現実の世界でいつ使用されますか?

現実の世界では、オッズ比は、研究者が 2 つのイベントが発生する確率を比較するさまざまな状況で使用されます。ここではいくつかの例を示します。

例 #1: オッズ比の解釈

研究者は、新しい治療法が既存の治療法と比べて患者の健康状態に良い影響を与える可能性を高めるかどうかを知りたいと考えています。次の表は、治療に応じて、健康状態にプラスまたはマイナスの結果を経験した患者の数を示しています。

患者が新しい治療法で良好な結果を経験する可能性は、次のように計算できます。

確率= P(陽性) / 1 – P(陽性) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1.25

患者が既存の治療で良好な結果を経験する可能性は、次のように計算できます。

確率= P(陽性) / 1 – P(陽性) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0.875

したがって、既存の治療法と比較して、新しい治療法で良好な結果が得られるオッズ比は次のように計算できます。

オッズ比= 1.25 / 0.875 = 1.428 。

これは、新しい治療法を使用して患者が良好な結果を得る確率は、既存の治療法を使用して患者が肯定的な結果を得る確率の1.428倍であることを意味すると解釈します。

言い換えれば、新しい治療法により陽性結果が得られる可能性は42.8%増加します。

例 #2: オッズ比の解釈

マーケティング担当者は、広告によって顧客が特定の商品を他の広告よりも頻繁に購入するかどうかを知りたいと考えています。つまり、各広告を 100 人に表示します。次の表は、見た広告に基づいて商品を購入した人の数を示しています。

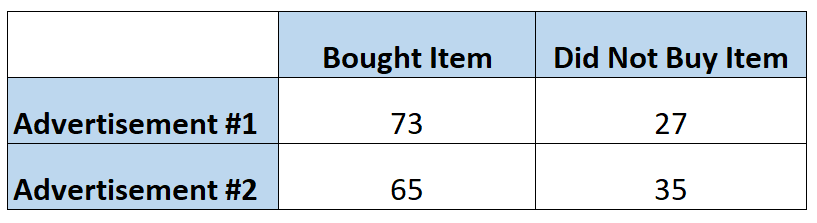
最初の広告を見た後に個人が商品を購入する可能性は次のように計算できます。

オッズ= P(買い) / 1 – P(買い) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2.704

個人が 2 番目の広告を見た後に商品を購入する可能性は、次のように計算できます。

オッズ= P(買い) / 1 – P(買い) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1.857

したがって、顧客が最初の広告を見た後に商品を購入する場合と、2 番目の広告を見た後に購入する場合のオッズ比は次のように計算できます。

オッズ比= 2.704 / 1.857 = 1.456 。

これは、個人が最初の広告を見た後に商品を購入する確率は、個人が 2 番目の広告を見た後に商品を購入する確率の1.456倍であることを意味すると解釈します。

つまり、最初の出品のおかげで商品が購入される可能性は45.6%増加します。

追加リソース

Excel でオッズ比と相対リスクを計算する方法
1 未満のオッズ比を解釈する方法
相対リスクをどう解釈するか