カイ二乗分布

によるベンジャミン・アンダーソン博士 8月 4, 2023 確率 0コメント

この記事では、カイ二乗分布とは何か、またその用途について説明します。さらに、カイ二乗分布グラフとそのプロパティも表示されます。

カイ二乗分布とは何ですか?

カイ二乗分布は、記号が χ² である確率分布です。より正確には、カイ二乗分布は、正規分布を持つk 個の独立確率変数の二乗の合計です。

したがって、カイ二乗分布にはk 個の自由度があります。したがって、カイ二乗分布は、それが表す正規分布変数の二乗和と同じくらいの自由度を持ちます。

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

カイ二乗分布は、ピアソン分布としても知られています。

カイ二乗分布はガンマ分布の特殊なケースであることに注意してください。

カイ二乗分布は、仮説検定や信頼区間などの統計的推論で広く使用されています。このタイプの確率分布がどのように応用されるかを以下で見ていきます。

カイ二乗分布グラフ

カイ二乗分布の定義を理解すると、このタイプの分布の例がいくつかグラフで表されることがわかります。以下では、カイ二乗分布の確率プロットが自由度に応じてどのように変化するかを示します。

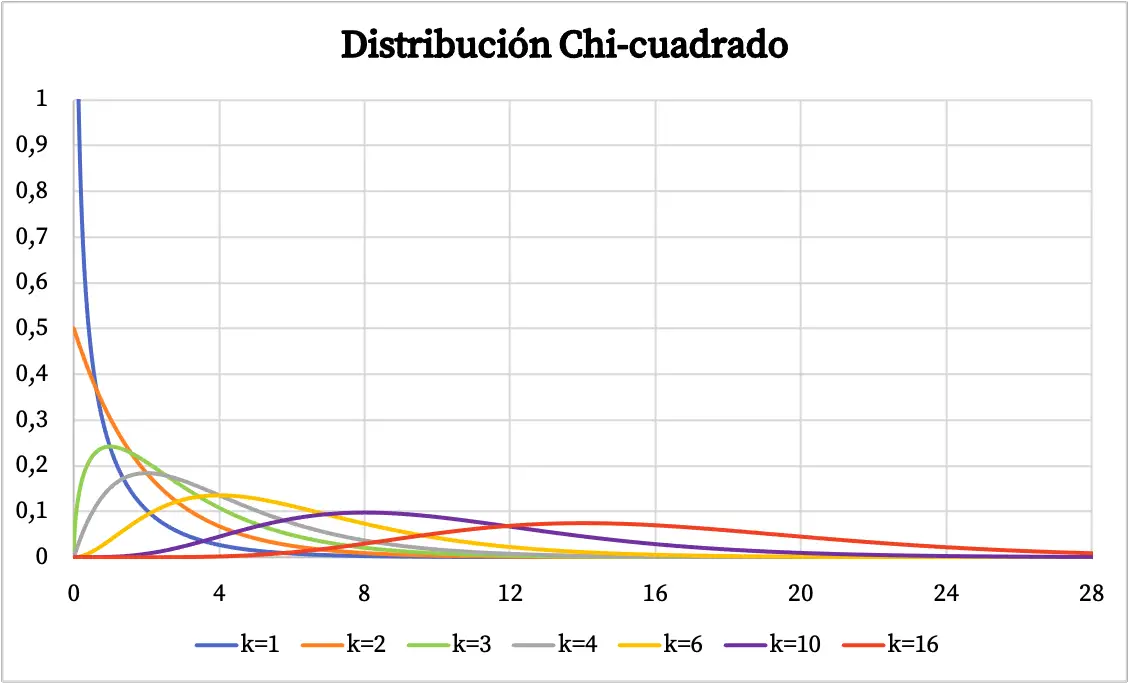
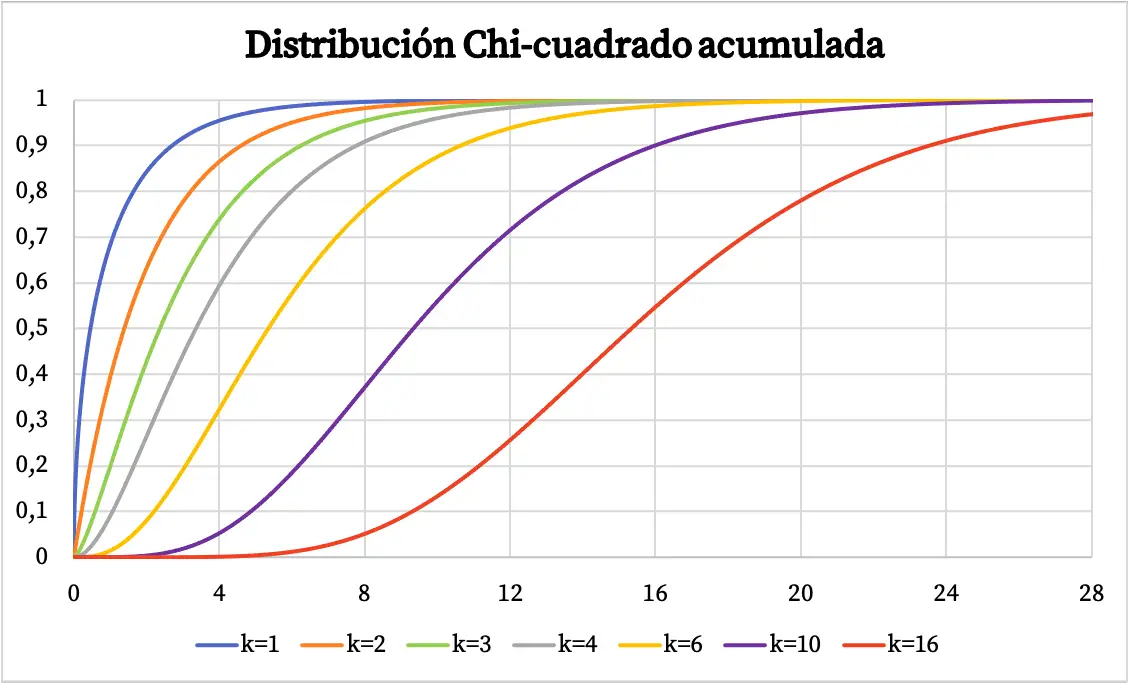
カイ二乗分布の密度関数は上のグラフに示されています。一方、カイ二乗累積確率分布関数のグラフは次のようになります。

➤参照:カイ二乗分布表

カイ二乗分布の特徴

このセクションでは、確率理論と統計に関連するカイ二乗分布の最も重要な特性を見ていきます。

カイ二乗分布の平均は、その自由度に等しくなります。

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

カイ二乗分布の分散は、分布の自由度の 2 倍に等しくなります。

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

カイ二乗分布の最頻値は、分布に複数の自由度がある限り、その自由度より 2 単位小さくなります。

$Mo=k-2 \qquad \text{si } k\geq 2$

x=0 の場合、カイ二乗分布の密度関数はゼロです。ただし、x の値が 0 より大きい場合、カイ二乗分布の密度関数は次の式で定義されます。

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

カイ二乗分布の累積分布関数は、次の式によって決まります。

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

カイ二乗分布の歪度係数は、8 を分布の自由度の数で割った商の平方根です。

$\displaystyle A=\sqrt{\frac{8}{k}}$

カイ二乗分布の尖度は、次の式を使用して計算されます。

$C=3+\cfrac{12}{k}$

中心極限定理により、 kが十分に大きい場合、カイ二乗分布は正規分布で近似できます。

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

カイ二乗分布の応用

カイ二乗分布は、統計学においてさまざまな用途に使用できます。実際、変数間の独立性と理論的分布への適合度をチェックするために使用されるカイ二乗検定さえあります。たとえば、カイ二乗検定を使用して、サンプルのデータがポアソン分布に準拠しているかどうかを判断できます。

線形回帰分析では、カイ二乗分布は、正規分布した母集団の平均を推定し、線形回帰分析の直線の傾きを推定するためにも使用されます。

最後に、カイ二乗分布も、Snedecor F 分布との関係を通じて分散分析に参加します。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る