分散によって何が説明されるのでしょうか? (定義&例)
説明された分散(「説明された変動」と呼ばれることもあります) は、モデルの予測変数によって説明できるモデル内の応答変数の分散を指します。
モデルの説明された分散が大きいほど、モデルが説明できるデータの変動が大きくなります。
説明された分散は、2 つの異なる統計モデルの結果に現れます。
1. ANOVA: 3 つ以上の独立したグループの平均を比較するために使用されます。
2. 回帰: 1 つ以上の予測変数と応答変数の間の関係を定量化するために使用されます。
次の例は、これらの各方法で残差分散を解釈する方法を示しています。
注: 説明された分散の逆は、残差分散と呼ばれます。
ANOVA モデルで説明される分散
ANOVA (分散分析) モデルを当てはめるたびに、次のような ANOVA テーブルが作成されます。
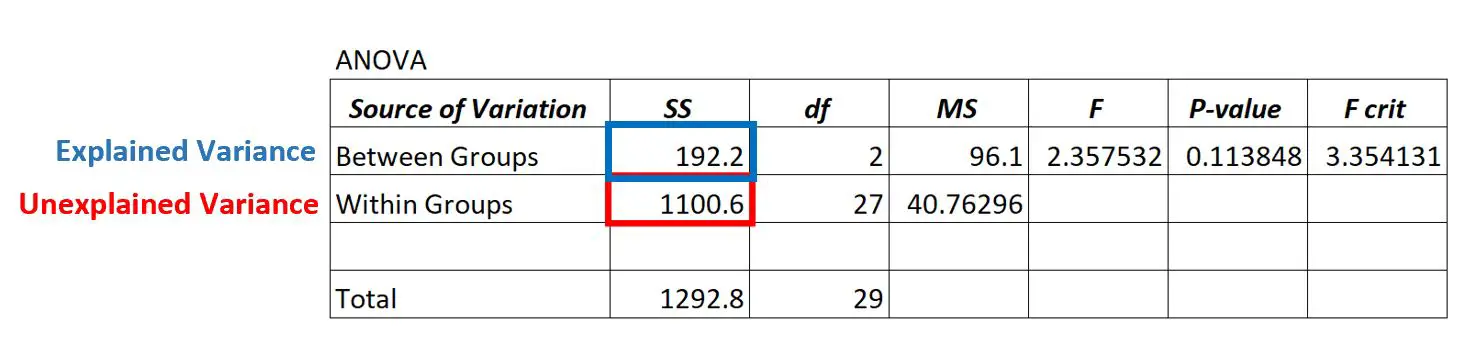
説明された分散は、 グループ間変動の SS (「平方和」) 列に表示されます。
上記の ANOVA モデルでは、説明された分散が 192.2 であることがわかります。
この説明分散が「高い」かどうかを判断するには、グループ内の平均二乗和とグループ間の平均二乗和を計算し、その 2 つの比を求めます。これにより、ANOVA 表の全体的な F 値が得られます。
- F = MSが入る/ MSが入る
- F = 96.1 / 40.76296
- F = 2.357
上記の ANOVA 表の F 値は 2.357 で、対応する p 値は 0.113848 です。
この p 値は α = 0.05 以上であるため、 ANOVA の帰無仮説を棄却する十分な証拠がありません。
これは、比較しているグループ間の平均差が大幅に異なると言える十分な証拠がないことを意味します。
これは、ANOVA モデルの説明された分散が説明のない分散と比較して小さいことを示しています。
回帰モデルで説明される分散
回帰モデルでは、説明された分散はR 二乗(多くの場合R2と書かれます) として要約されます。
この値は、モデル内の予測変数によって説明できる応答変数の分散の割合を表します。
R 二乗の値の範囲は 0 から次のとおりです。
- 値0は、応答変数が予測変数によってまったく説明できないことを示します。
- 値1は、応答変数が予測変数によって誤差なく完全に説明できることを示します。
回帰モデルを当てはめると、通常は次のような結果が得られます。
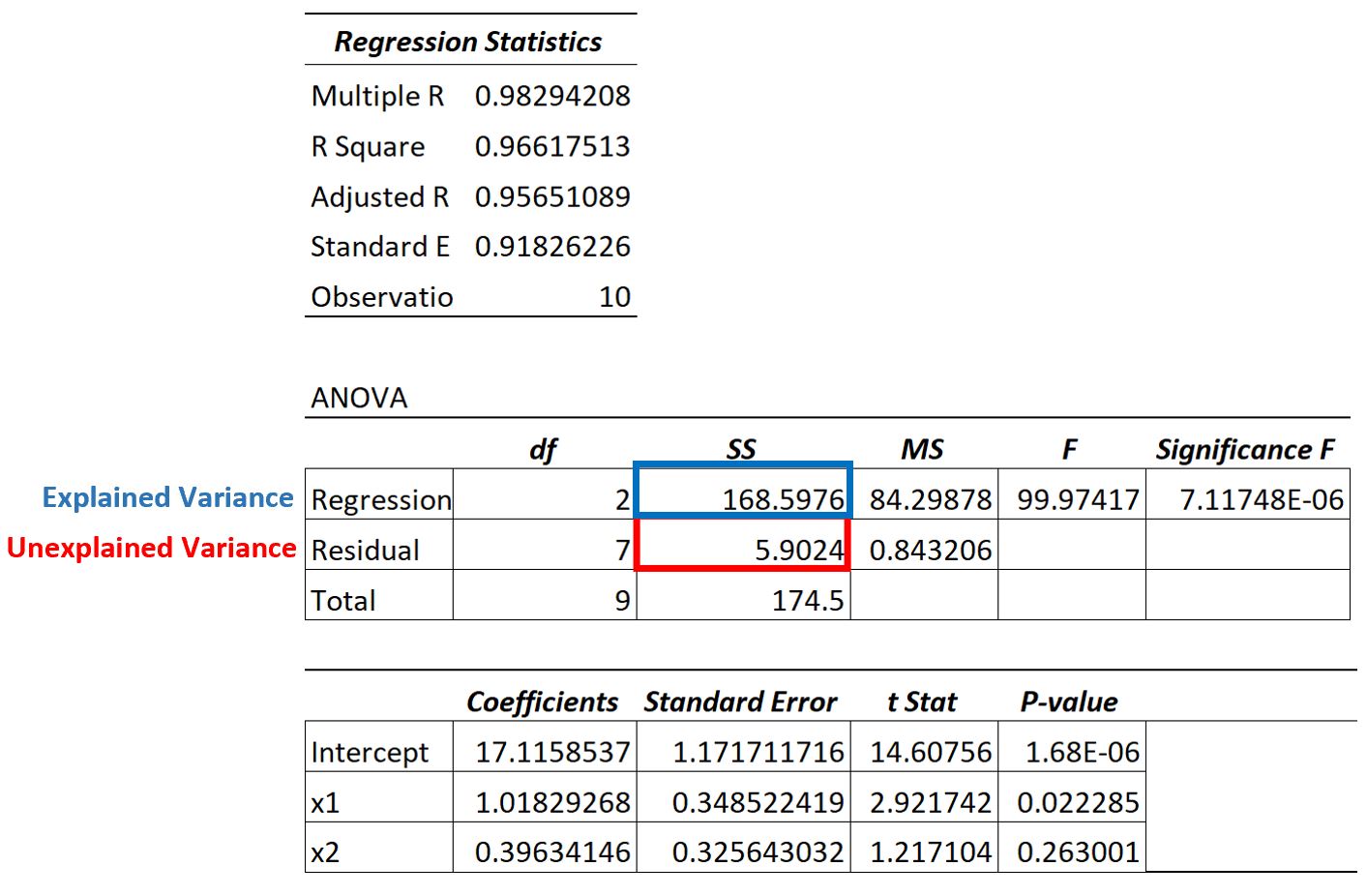
説明された分散は168.5976で、合計分散は174.5であることがわかります。
これらの値を使用すると、この回帰モデルの R 二乗値を次のように計算できます。
- R の二乗: 回帰 SS / 合計 SS
- R二乗: 168.5976 / 174.5
- R二乗: 0.966
このモデルの R 二乗値は 1 に近いため、モデルで説明される分散が非常に高いことがわかります。
言い換えれば、モデルは、予測変数を使用して応答変数の変動を説明するという点でうまく機能します。