度数分布でクラスの中点を見つける方法
度数分布表は、さまざまなクラスのデータの度数を表示する表です。
たとえば、次の度数分布表は、5 つの異なるクラスの度数を示しています。
| クラス | 頻度 |
|---|---|
| 1~10 | 20 |
| 11~20 | 21 |
| 21~30 | 16 |
| 31 – 40 | 5 |
| 41 – 50 | 4 |
各クラスの中点は、クラスの下限と上限を加算し、2 で割ることによって求めることができます。
クラス中間点= (クラスの下限値 + クラスの上限値) / 2
次の表は、各クラスの中点を計算する方法を示しています。
| クラス | 頻度 | 中間点 |
|---|---|---|
| 1~10 | 20 | (1+10) / 2 |
| 11~20 | 21 | (11+20) / 2 |
| 21~30 | 16 | (21+30) / 2 |
| 31 – 40 | 5 | (31+40) / 2 |
| 41 – 50 | 4 | (41+50) / 2 |
したがって、次の中間点が残ります。
| クラス | 頻度 | 中間点 |
|---|---|---|
| 1~10 | 20 | 5.5 |
| 11~20 | 21 | 15.5 |
| 21~30 | 16 | 25.5 |
| 31 – 40 | 5 | 35.5 |
| 41 – 50 | 4 | 45.5 |
クラス中間点はいつ使用されますか?
クラス中間点は、ヒストグラムを作成して度数表の値を視覚化する場合によく使用されます。
ヒストグラムでは、グラフの X 軸に沿ってクラスがリストされ、バーを使用して Y 軸に沿って各クラスの頻度が表されます。各バーはそのクラスの中央に配置されます。
次のヒストグラムは、前の度数表のデータを視覚的に表現したものです。
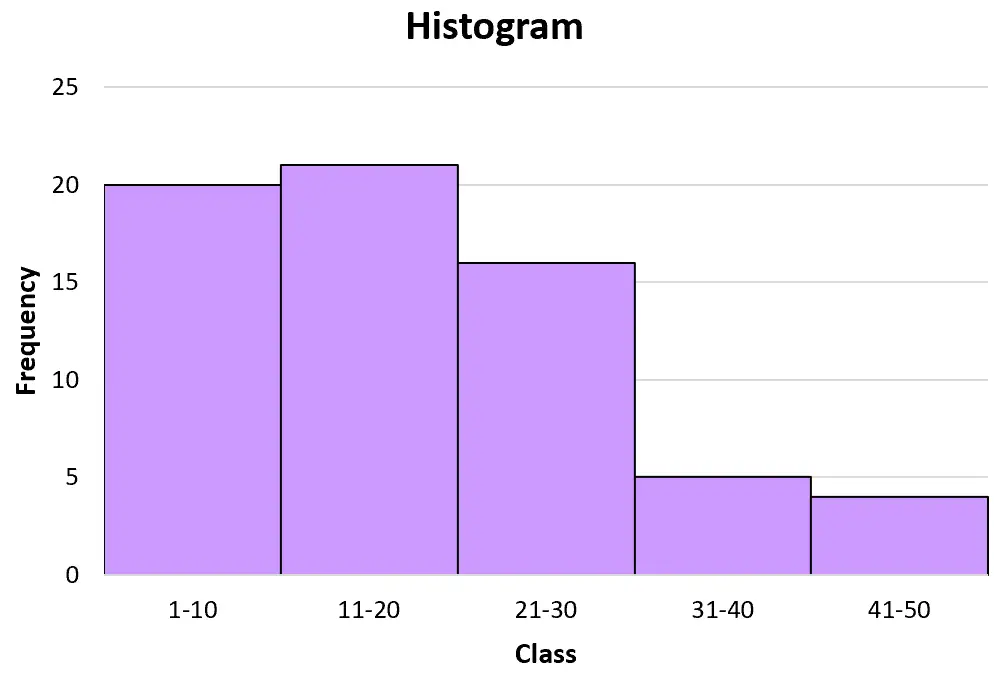
各バーがクラスの中央にどのように配置されているかに注目してください。
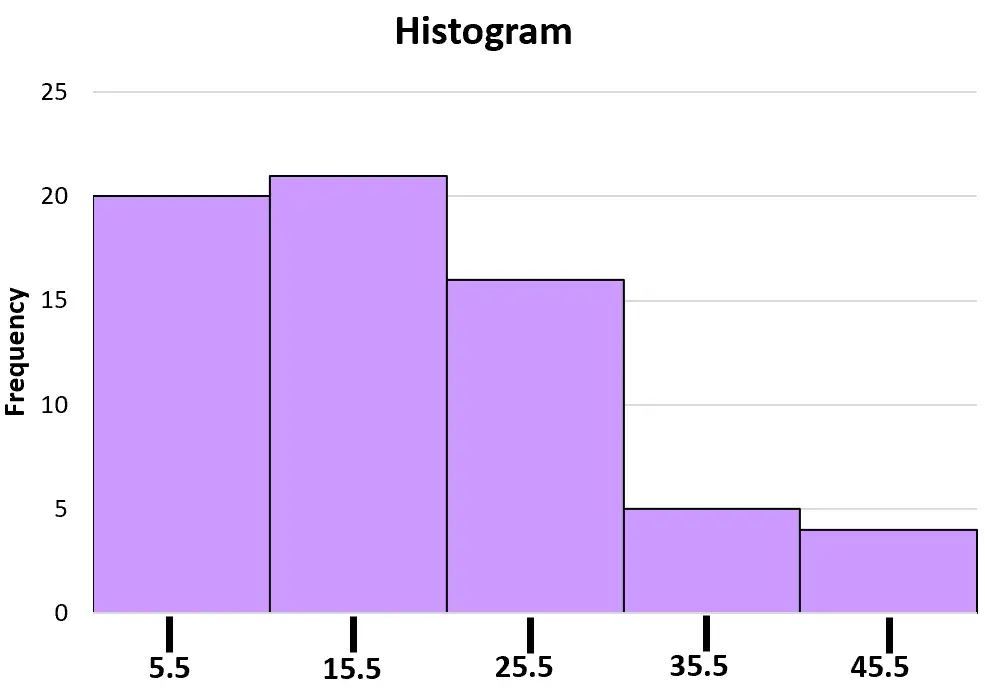
ヒストグラムを手動で作成する場合、バーを配置する場所を知るために、クラスの中点を知っておくと特に役立ちます。
ただし、ほとんどの統計ソフトウェアは、ヒストグラムのバーをクラスの中間点を中心に自動的に中心に配置できるため、通常はこれらの中間点を自分で手動で見つける必要はありません。