Sas でクラスカル・ウォリス検定を実行する方法
クラスカル・ウォリス検定は、 3 つ以上の独立したグループの中央値間に統計的に有意な差があるかどうかを判断するために使用されます。
これは、一元配置 ANOVAと同等のノンパラメトリックとみなされます。
このチュートリアルでは、SAS で Kruskal-Wallis テストを実行する方法の段階的な例を示します。
ステップ 1: データを入力する
研究者が、3 つの異なる肥料が異なるレベルの植物の成長につながるかどうかを知りたいと考えているとします。
彼らは 30 個の異なる植物をランダムに選択し、10 個ずつ 3 つのグループに分け、各グループに異なる肥料を適用します。 1 か月後、各植物の高さを測定します。
次のデータを SAS に入力します。これは、各グループの 10 本の植物の合計成長 (インチ単位) を示します。
/*create dataset*/
data fertilizer_data;
input fertilizer $growth;
datalines ;
fert1 7
fert1 14
fert1 14
fert1 13
fert1 12
fert1 9
fert1 6
fert1 14
fert1 12
fert1 8
fert2 15
fert2 17
fert2 13
fert2 15
fert2 15
fert2 13
fert2 9
fert2 12
fert2 10
fert2 8
fert3 6
fert3 8
fert3 8
fert3 9
fert3 5
fert3 14
fert3 13
fert3 8
fert3 10
fert3 9
;
run ;
ステップ 2: クラスカル-ウォリス検定を実行する
次に、 proc npar1wayステートメントを使用してクラスカル-ウォリス検定を実行し、3 つの肥料グループ間の植物の成長の中央値を比較します。
/*perform Kruskal-Wallis test*/
proc npar1way data =fertilizer_data wilcoxon dscf ;
class fertilizer;
vargrowth ;
run ;
ステップ 3: 結果を解釈する
結果の最初の表は、全体的なカイ二乗検定統計量と、クラスカル-ウォリス検定の対応する p 値を示しています。
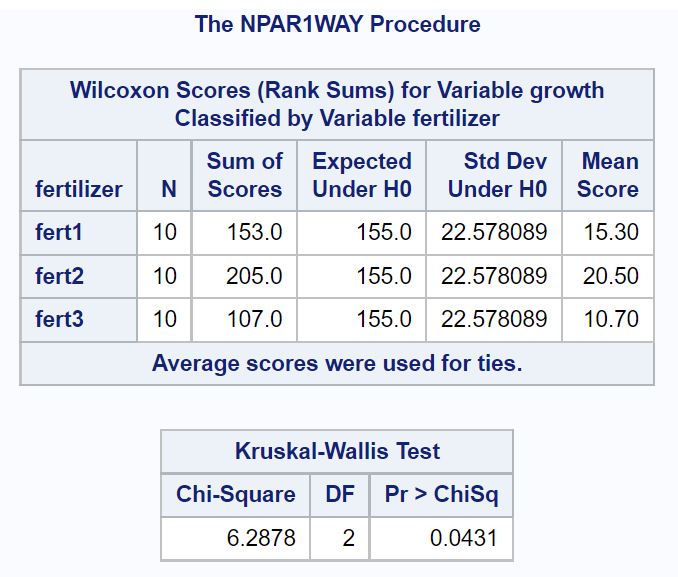
検定の p 値は0.0431です。この値は 0.05 未満であるため、植物の成長の中央値が 3 つの肥料すべてで同じであるという帰無仮説を棄却します。
これは、使用される肥料の種類が植物の成長に統計的に有意な差を引き起こすと結論付けるのに十分な証拠があることを意味します。
最終的な結果の表には、3 つのグループそれぞれの間のペアごとの比較の p 値が表示されます。
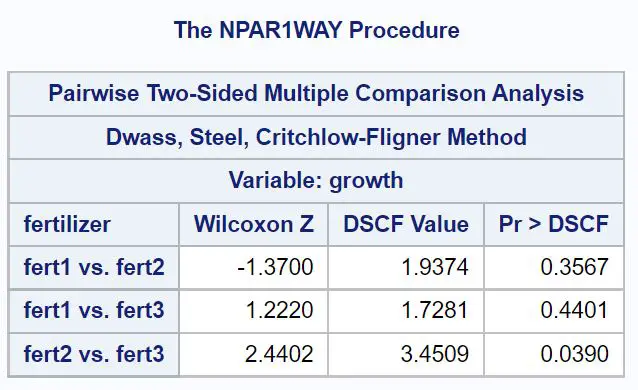
この表から、0.05 を下回る唯一の p 値は肥料 2 と肥料 3 の比較であり、その p 値は0.0390であることがわかります。
これは、肥料 2 と肥料 3 の間には植物の成長に統計的に有意な差があるが、他のペア比較の間には差がないことを意味します。
追加リソース
次のチュートリアルでは、SAS で他の一般的な統計テストを実行する方法について説明します。
SAS で 1 サンプルの t 検定を実行する方法
SAS で 2 サンプルの t 検定を実行する方法
SAS で一元配置分散分析を実行する方法
SAS で二元配置分散分析を実行する方法