Cramer's v を解釈する方法 (例付き)
Cramer’s V は、 2 つの名目変数間の関連の強さの尺度です。
0 から 1 まで変化します。
- 0 は、 2 つの変数間に関連性がないことを示します。
- 1 は、 2 つの変数間の完全な関連性を示します。
次のように計算されます。
クラマーの V = √ (X 2 /n) / min(c-1, r-1)
金:
- X 2 :カイ二乗統計量
- n:合計サンプルサイズ
- r:行数
- c:列数
Cramer’s V をどう解釈するか
次の表は、自由度に応じて Cramer’s V を解釈する方法を示しています。
| 自由度 | 少し | 平均 | 大きい |
|---|---|---|---|
| 1 | 0.10 | 0.30 | 0.50 |
| 2 | 0.07 | 0.21 | 0.35 |
| 3 | 0.06 | 0.17 | 0.29 |
| 4 | 0.05 | 0.15 | 0.25 |
| 5 | 0.04 | 0.13 | 0.22 |
次の例は、さまざまな状況で Cramer’s V を解釈する方法を示しています。
例 1: 2×3 配列に対する Cramer の V の解釈
目の色と性別の間に関連性があるかどうかを知りたいとします。したがって、50 人に質問し、次の結果が得られます。
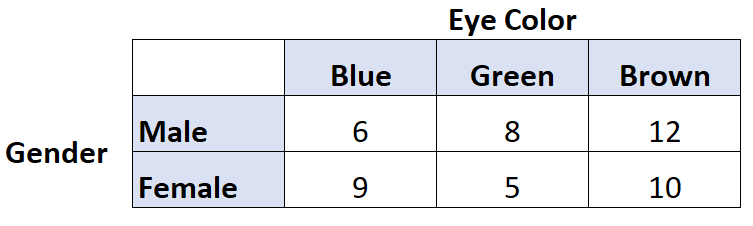
R で次のコードを使用して、これら 2 つの変数の Cramer’s V を計算できます。
library (rcompanion) #create table data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 ) #view table data [,1] [,2] [,3] [1,] 6 8 12 [2,] 9 5 10 #calculate Cramer's V cramerV(data) Cramer V 0.1671
Cramer の V は0.1671であることがわかります。
自由度は次のように計算されます。
- df = min(#行-1, #列-1)
- df = 分(1, 2)
- df = 1
上の表を参照すると、Cramer’s V が0.1671で自由度 = 1ということは、目の色と性別の間に小さな (または「弱い」) 関連性があることを示していることがわかります。
例 2: 3×3 テーブルの Cramer の V の解釈
目の色と政党の好みとの間に関連性があるかどうかを知りたいとします。したがって、50 人に質問し、次の結果が得られます。
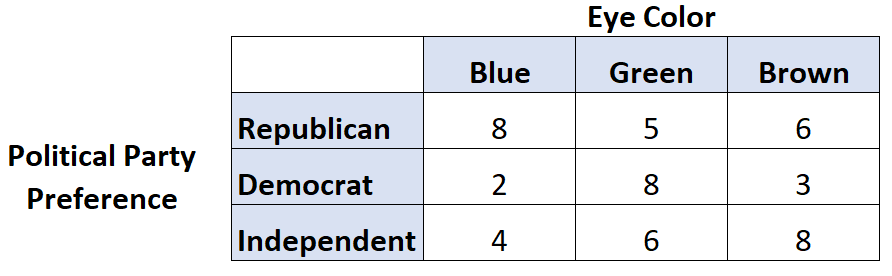
R で次のコードを使用して、これら 2 つの変数の Cramer’s V を計算できます。
library (rcompanion) #create table data = matrix(c(8, 2, 4, 5, 8, 6, 6, 3, 8), nrow= 3 ) #view table data [,1] [,2] [,3] [1,] 8 5 6 [2,] 2 8 3 [3,] 4 6 8 #calculate Cramer's V cramerV(data) Cramer V 0.246
Cramer の V は0.246であることがわかります。
自由度は次のように計算されます。
- df = min(#行-1, #列-1)
- df = 分(2, 2)
- df = 2
上の表を参照すると、クラマーの V が0.246で自由度 = 2であるため、目の色と政党の好みの間に中程度 (または「中程度」) の関連があることがわかります。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアで Cramer’s V を計算する方法を説明します。
Excel でクラマーの V を計算する方法
R で Cramer の V を計算する方法
Python で Cramer’s V を計算する方法