サンプルの割合

この記事では、統計における標本比率とは何かについて説明します。したがって、標本比率の計算方法、解決された演習、さらに標本比率と母集団比率の違いがわかります。

サンプルの割合はどのくらいですか?

サンプル比率は、サンプルサイズに対するサンプル内の成功事例の比率です。したがって、サンプルの割合を計算するには、サンプル内の成功数をデータの総数で割る必要があります。

サンプル比率の記号は次のとおりです。

。

統計では、調査を実施する場合、通常、母集団データのすべてがわかっているわけではありません。そのため、通常は代表的なサンプルの研究が実行され、その後、導き出された結論が母集団全体に外挿されます。人口。したがって、サンプルの割合は母集団全体の割合を推定するために使用されます。以下では、これがどのように行われるかを見ていきます。

比例式の例

サンプルの割合は、サンプル内の成功ケースの数をサンプル サイズで割ったものに等しくなります。したがって、サンプル比率を計算する式は次のようになります。

金：

• 

  はサンプルの割合です。

• 

  サンプル内の成功したケースの数です。

• 

  サンプル内のデータ項目の総数です。

割合計算例

サンプル比率の定義とその公式を理解した後、このセクションではサンプル比率がどのように計算されるかを理解できるように簡単な例を解いていきます。

• ある企業がおもちゃを製造し、その部品の 1 つを別の外部企業から購入します。しかし、購入したバッチの中に欠陥部品が出現するため、状態の良い部品の割合と欠陥の割合を調べる統計調査を実行することにしました。したがって、1,000 個のサンプルを注文すると、138 個の欠陥部品が見つかりました。サンプル中の良好な状態の部品の割合はどれくらいですか?また、サンプル中の不良品の割合はどのくらいでしょうか?

サンプル内の損傷していない部品の数は、1000 から欠陥のある部品の数を引いたものになります。

したがって、サンプルの割合を見つけるには、上で見た式を適用します。

したがって、良好な状態の部品のサンプルの割合は 86.2% になります。

一方、不良部品の割合は、1 から良品の割合を引いたものと等価です。

したがって、欠陥部品のサンプル割合は 13.8% になります。

サンプル割合と母集団割合

人口比率は統計上の母集団の比率です。つまり、母集団の割合は、母集団の一部であるすべての要素との関連で調査された母集団の成功事例の関係です。

したがって、国別割合と人口割合の違いは、国別割合が過半数の事例の割合であるのに対し、人口割合は人口のすべての要素に関する事象の事例の割合を指します。

サンプルの割合と母集団の割合を区別するために、それらは異なる記号で表されます。サンプル比率の記号は次のとおりです。

、人口比率の記号は

。

一般に、すべての母集団の値がわかっているわけではないため、母集団の割合を正確に決定することはできません。代わりに、母集団比率の値は通常、次の式の信頼区間を使用して推定されます。

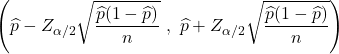
人口比率の推定方法を確認するには、次のリンクをクリックしてください。

割合の標本分布

最後に、比率の標本分布がどのような構成になっているかを見ていきます。これは標本比率に関連する統計的な概念です。

まず、標本分布とは何かを定義することから始めます。標本分布は、統計母集団から考えられるすべてのサンプルを考慮して得られる分布です。

したがって、割合の標本分布は、母集団から考えられる各標本の割合を計算した結果得られる分布です。つまり、母集団から考えられるすべてのサンプルを調査し、各サンプルの割合を計算すると、計算された一連の値がサンプル割合の標本分布になります。