サンプル平均
この記事では、統計における標本平均とは何かについて説明します。同様に、サンプルの平均を計算する方法、解決された演習、さらにサンプルの平均を計算するためのオンライン計算機も見つかります。
サンプルってどういう意味ですか?
統計における標本平均とは、標本内の値の平均です。サンプル平均を計算するには、サンプル内のすべての値を加算し、サンプル内のデータの総数で割る必要があります。
標本平均の記号は次のとおりです。
![]()
。
統計研究では、一般に母集団のすべての値がわかっているわけではありません。そのため、母集団のサンプルが選択されて分析され、得られた結論が母集団全体に推定されます。したがって、サンプル平均は母集団平均を推定するために使用されます。
平均計算式の例
サンプル平均は、すべてのサンプル値の合計をサンプルサイズで割ったものに等しくなります。つまり、サンプル平均を計算するには、サンプル内のすべての値を加算し、サンプル内のデータの総数で割ります。
したがって、サンプル平均を計算する式は次のようになります。

👉以下の計算機を使用して、任意のデータセットのサンプル平均を計算できます。
標本平均は標本からのデータを使用して計算されるため、母集団平均の値は計算値と異なる場合があることに注意してください。
サンプル平均値の計算例
サンプル平均の定義とその公式がわかったので、簡単な例を解いてデータセットからサンプル平均を取得する方法を見てみましょう。
- ホセは市内中心部に引っ越したいと考えていますが、あまり時間がないため、すべての賃貸アパートの価格を分析することはできません。そこで、ダウンタウンに住むのにどれくらいの費用がかかるかを調べるために、5 つのアパート (以下を参照) の賃貸料だけを調べることにしました。サンプルの平均価格はいくらですか?
€600 €430 €820 €575 €950
標本平均を求めるには、すべての標本値を合計し、観測値の合計数である 5 で割る必要があります。そこで、標本平均の公式を適用します。
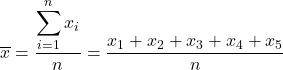
次に、データを式に代入してサンプル平均を計算します。
![]()
つまり、サンプルとして選択されたアパートのサンプルの平均価格は 675 ユーロです。
平均計算の例
統計サンプルのデータを次の計算機に入力して、サンプル平均を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
サンプル平均と母集団平均
母集団の平均は、統計上の母集団の平均です。したがって、母集団平均は、統計調査の実行対象となるすべての要素の平均です。
したがって、サンプル平均と母集団平均の違いは、サンプル平均がサンプル値の平均であるのに対し、母集団平均は母集団内の値の平均であることです。
標本平均と母集団平均を区別するために、それらは異なる記号で表されます。標本平均の記号は次のとおりです。
![]()
, 一方、母集団平均の記号は
![]()
。
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e9047d35ec6ee8da3cb57e5134837876_l3.png)
標本平均は母集団平均の値を推定するために使用されます。これは、点推定または区間推定を使用して行うことができます。
標本平均の標本分布
最後に、標本の平均値の標本分布がどのようなものかを見てみましょう。統計上の概念は混乱を招く可能性があるためです。
まず、標本分布とは何かを定義することから始めます。標本分布は、統計母集団から考えられるすべてのサンプルを考慮して得られる分布です。
したがって、標本平均の標本分布は、母集団から考えられる各標本の平均を計算した結果の分布になります。つまり、母集団から考えられるすべてのサンプルを調査し、各サンプルの平均を計算すると、計算された値のセットがサンプル平均の標本分布となります。
結論として、標本平均と標本分布は似た名前ですが、それらを区別する方法を知る必要があります。標本平均は標本から計算される統計パラメータですが、一方、標本分布は分布です。それは、母集団から作成できるすべてのサンプルを研究した結果です。