Excel で 1 サンプルの t 検定を実行する方法
1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。
このチュートリアルでは、Excel で 1 サンプルの t 検定を実行する方法を説明します。
Excel で 1 サンプルの t 検定を実行する方法
植物学者が、特定の種の植物の平均高さが 15 インチに等しいかどうかを知りたいとします。彼女は 12 本の植物から無作為にサンプルを採取し、それぞれの高さをインチ単位で記録しました。
次の画像は、サンプル内の各植物の高さ (インチ単位) を示しています。
次の手順を使用して 1 サンプルの t 検定を実行し、この植物種の平均高さが実際に 15 インチであるかどうかを判断できます。
ステップ 1: サンプル サイズ、サンプル平均、サンプル標準偏差を見つけます。
まず、サンプル サイズ、サンプル平均、サンプル標準偏差を見つける必要があります。これらはすべて 1 サンプルの t 検定を実行するために使用されます。
次の図は、これらの値の計算に使用できる式を示しています。
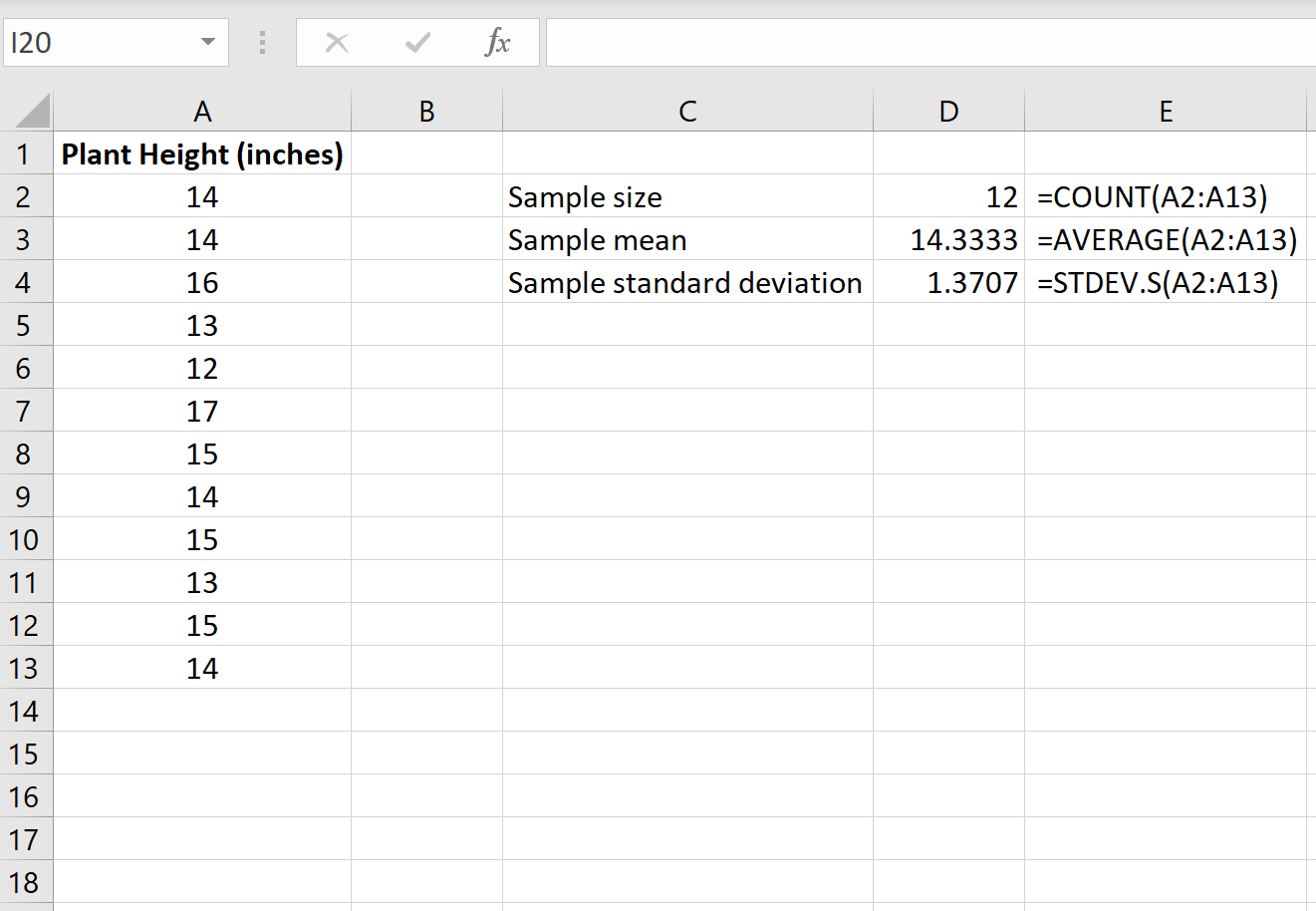
ステップ 2: t検定統計量を計算します。
次に、次の式を使用してt検定統計量を計算します。
t = x – μ / (s/ √n )
金:
x = サンプル平均
μ = 仮定の母集団平均
s = サンプル標準偏差
n = サンプルサイズ
次の図は、Excel でt を計算する方法を示しています。
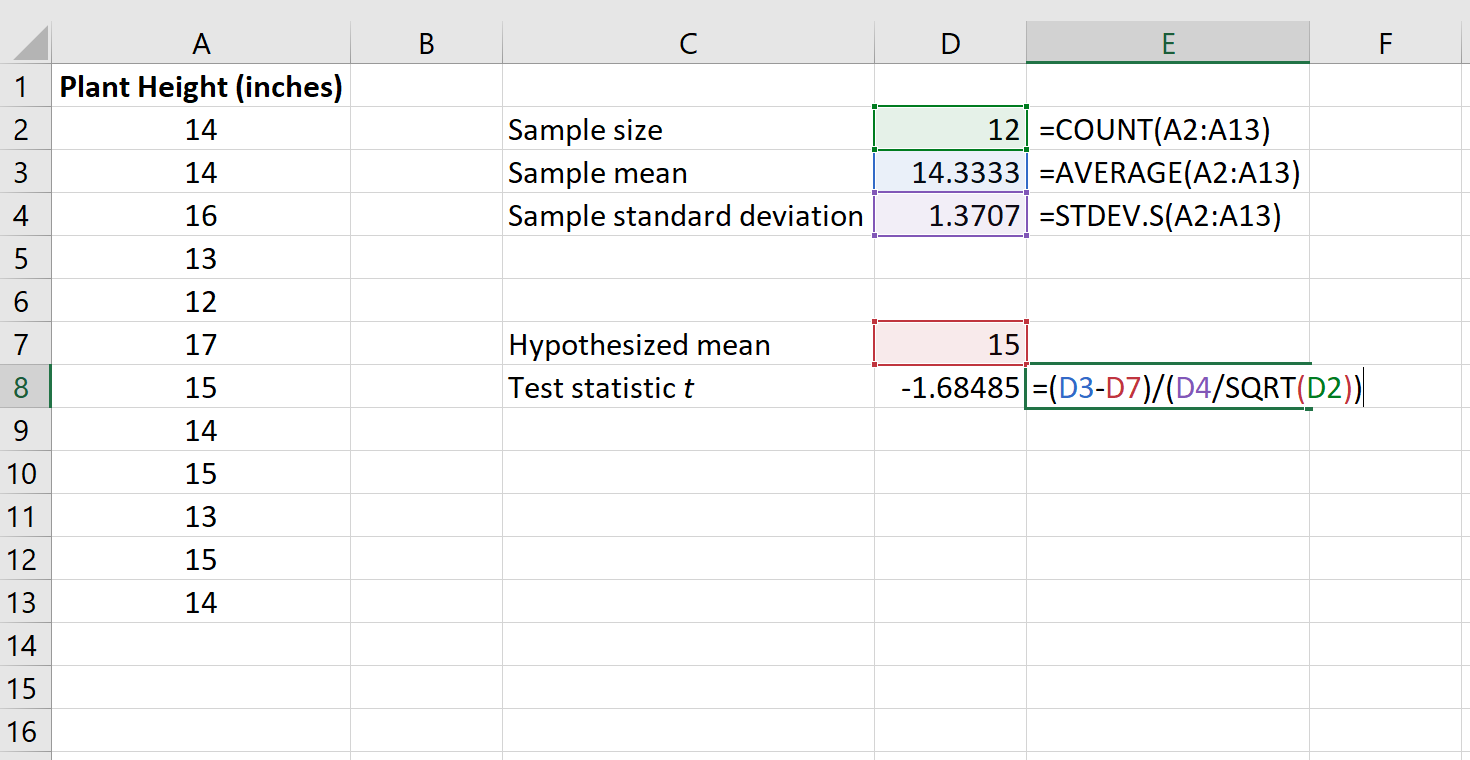
t検定統計量は-1.68485であることがわかります。
ステップ 3: 検定統計量の p 値を計算します。
次に、Excel の次の関数を使用して、検定統計量に関連付けられた p 値を計算する必要があります。
=T.DIST.2T(ABS(x), 自由度)
金:
x = t検定統計量
deg_freedom = テストの自由度、n-1 として計算
技術的なメモ:
T.DIST.2T()関数は、両側 t 検定の p 値を返します。代わりに左または右の t 検定を実行する場合は、代わりにそれぞれT.DIST()関数またはT.DIST.RT()関数を使用します。
次の図は、検定統計量の p 値を計算する方法を示しています。
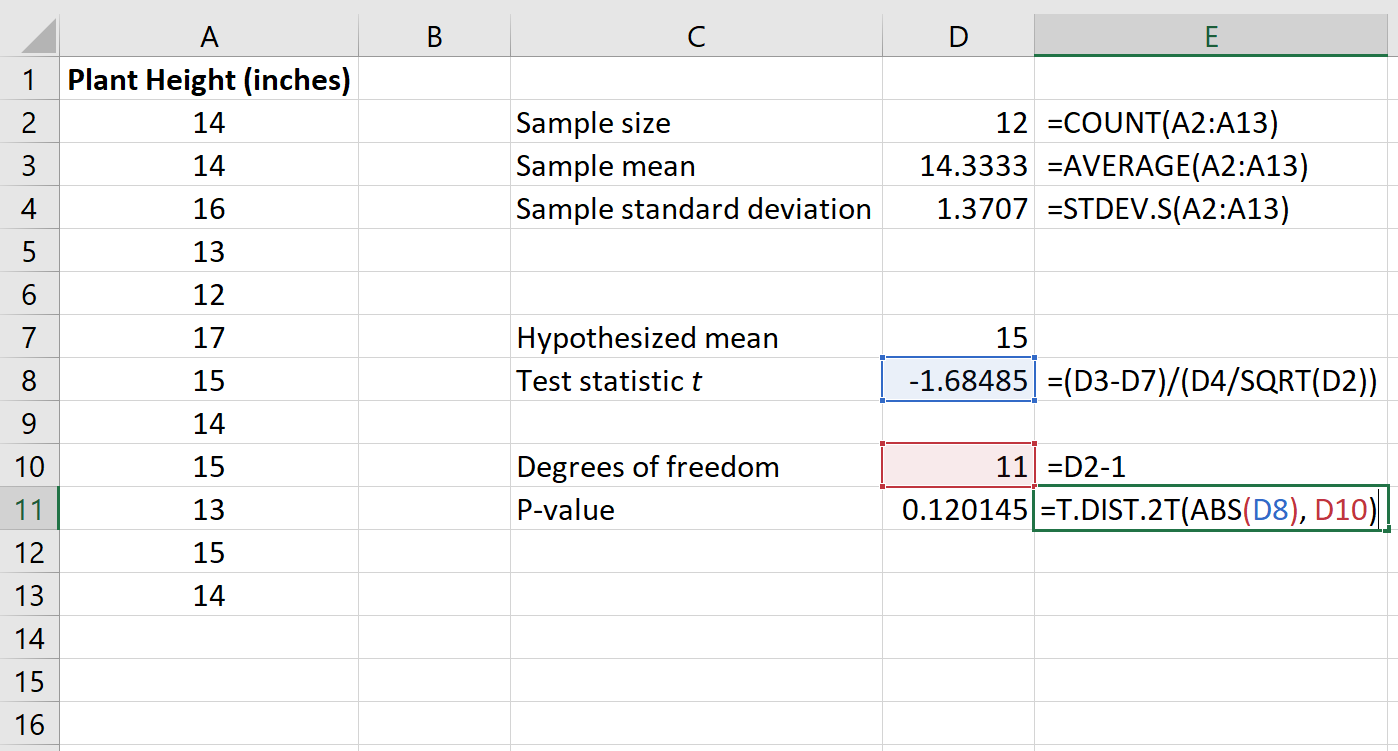
p 値は0.120145であることがわかります。
ステップ 4: 結果を解釈します。
特定のサンプルに対するこの t 検定の 2 つの仮説は次のとおりです。
H 0 : μ = 15 (この植物種の平均高さは 15 インチ)
H A : μ ≠15 (平均身長は 15 インチではありません)
検定の p 値(0.120145)は alpha = 0.05 より大きいため、検定の帰無仮説を棄却できません。
この特定の種の植物の平均高さが 15 インチ以外であると言える十分な証拠はありません。
追加リソース
次のチュートリアルでは、Excel で他の一般的なタイプの t 検定を実行する方法について説明します。