Ti-84 電卓で 1 サンプルの t 検定を実行する方法
1 サンプル t 検定は、母集団の平均が特定の値に等しいかどうかを検定するために使用されます。
このチュートリアルでは、TI-84 電卓で 1 サンプルの t 検定を実行する方法を説明します。
例: TI-84 電卓でのサンプル t 検定
研究者は、特定の種類の自動車が 1 ガロンあたり 20 マイルの速度を達成できるかどうかを知りたいと考えています。 74 台の車から無作為にサンプルを取得し、平均が 21.29 mpg で、標準偏差が 5.78 mpg であることがわかりました。このデータを使用して 1 サンプルの t 検定を実行し、このタイプの車の実際の mpg が 20 mpg に等しいかどうかを判断します。
ステップ 1: T テストを選択します。
「統計」をタップします。 「テスト」まで下にスクロールします。 「T-Test」までスクロールし、 ENTERを押します。
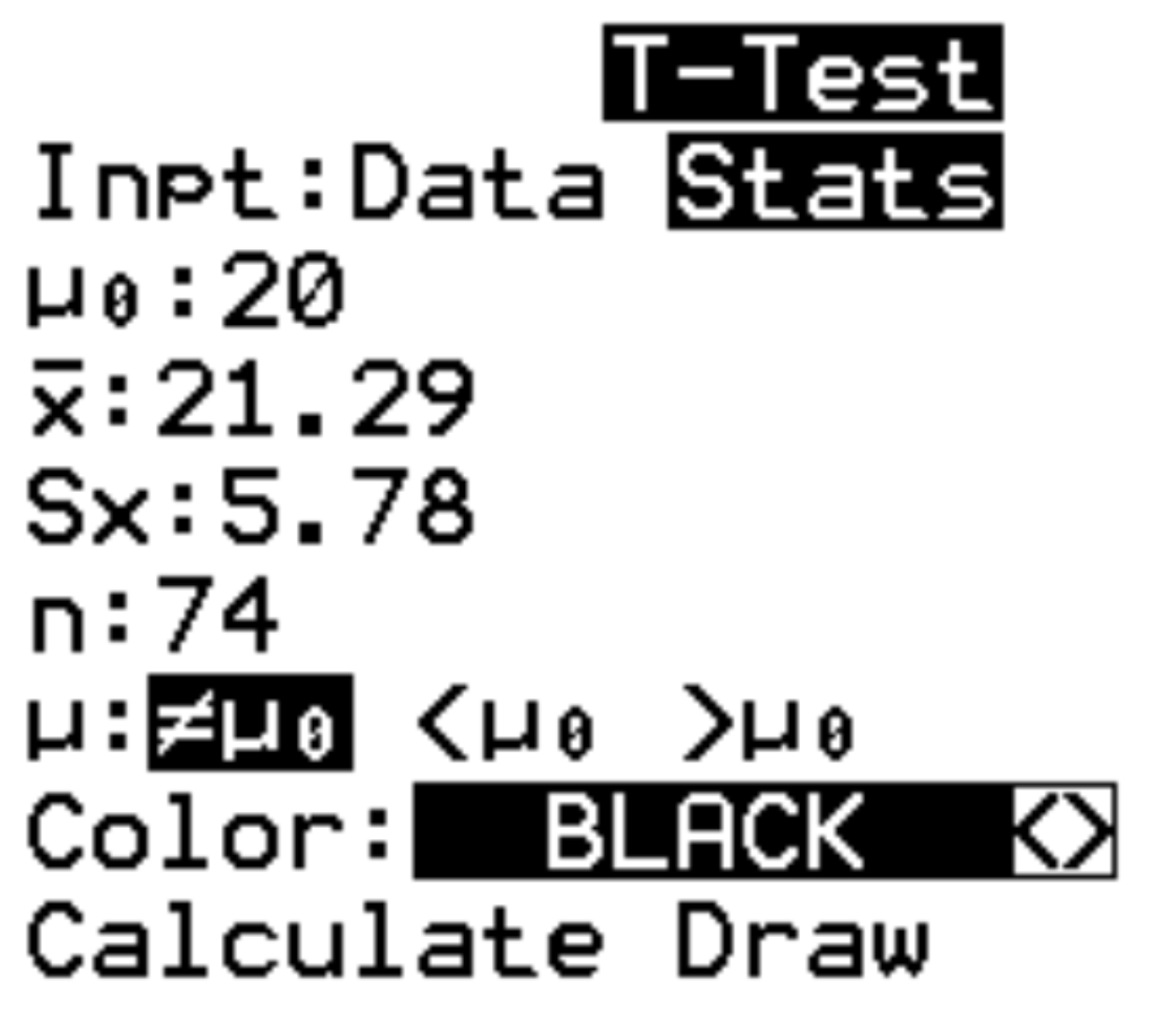
ステップ2: 必要な情報を入力します。
計算機は次の情報を要求します。
- 入力:生データ (データ) を使用するか、要約統計量 (統計) を使用するかを選択します。この場合、「統計」を強調表示してENTERを押します。
- μ 0 :帰無仮説で使用する平均。 20 と入力してENTERを押します。
- × :サンプルの意味。 21.29 と入力してENTERを押します。
- s x : サンプルの標準偏差。 5.78 と入力してENTERを押します。
- n : サンプルサイズ。 74 と入力してENTERを押します。
- μ : 使用する対立仮説。両側検定を実行しているため、 ≠ μ 0を強調表示してENTERを押します。これは、対立仮説が μ≠20 であることを示しています。他の 2 つのオプションは、左側のテスト (<μ 0 ) と右側のテスト (>μ 0 ) に使用されます。
最後に、「計算」を強調表示してENTERを押します。
ステップ 3: 結果を解釈します。
私たちの計算機は、1 サンプルの t 検定の結果を自動的に生成します。

結果を解釈する方法は次のとおりです。
- μ≠20 : これは検定の対立仮説です。
- t=1.919896124 : これは t 検定統計量です。
- p=0.0587785895 : これは検定統計量に対応する p 値です。
- x =21.59 。これは私たちが採取した平均サンプルです。
- sx =5.78 。これは、入力したサンプル標準偏差です。
- n=74 : これは入力したサンプルサイズです。
検定の p 値 (0.0587785895) は 0.05 未満ではないため、帰無仮説を棄却できません。これは、このタイプの車の平均燃費が 20 mpg 以外であると言える十分な証拠がないことを意味します。