R で shapiro-wilk テストを実行する方法 (例付き)
シャピロ・ウィルク検定は正規性の検定です。これは、サンプルが正規分布に由来するかどうかを判断するために使用されます。
このタイプの検定は、特定のデータセットが正規分布に由来するかどうかを判断するのに役立ちます。これは、回帰、 ANOVA 、 t 検定など、多くの統計検定で一般的に使用される仮定です。 「その他。
R の次の組み込み関数を使用すると、特定のデータセットに対して Shapiro-Wilk テストを簡単に実行できます。
シャピロ.テスト(x)
金:
- x:データ値の数値ベクトル。
この関数は、 W検定統計量と対応する p 値を生成します。 p 値が α = 0.05 未満の場合、サンプルが正規分布した母集団からのものではないという十分な証拠があります。
注: shapiro.test() 関数を使用するには、サンプル サイズは 3 ~ 5,000 である必要があります。
このチュートリアルでは、この機能の実際の使用例をいくつか示します。
例 1: 正規データに対する Shapiro-Wilk 検定
次のコードは、サンプル サイズ n=100 のデータセットに対して Shapiro-Wilk 検定を実行する方法を示しています。
#make this example reproducible set.seed(0) #create dataset of 100 random values generated from a normal distribution data <- rnorm(100) #perform Shapiro-Wilk test for normality shapiro.test(data) Shapiro-Wilk normality test data:data W = 0.98957, p-value = 0.6303
検定の p 値は0.6303であることがわかります。この値は 0.05 未満ではないため、サンプル データは正規分布した母集団からのものであると想定できます。
平均 = 0、標準偏差 = 1 の正規分布からランダムな値を生成する rnorm() 関数を使用してサンプル データを生成したため、この結果は驚くべきことではありません。
関連: R の dnorm、pnorm、qnorm、および rnorm のガイド
ヒストグラムを作成して、サンプル データが正規分布していることを視覚的に検証することもできます。
hist(data, col=' steelblue ')
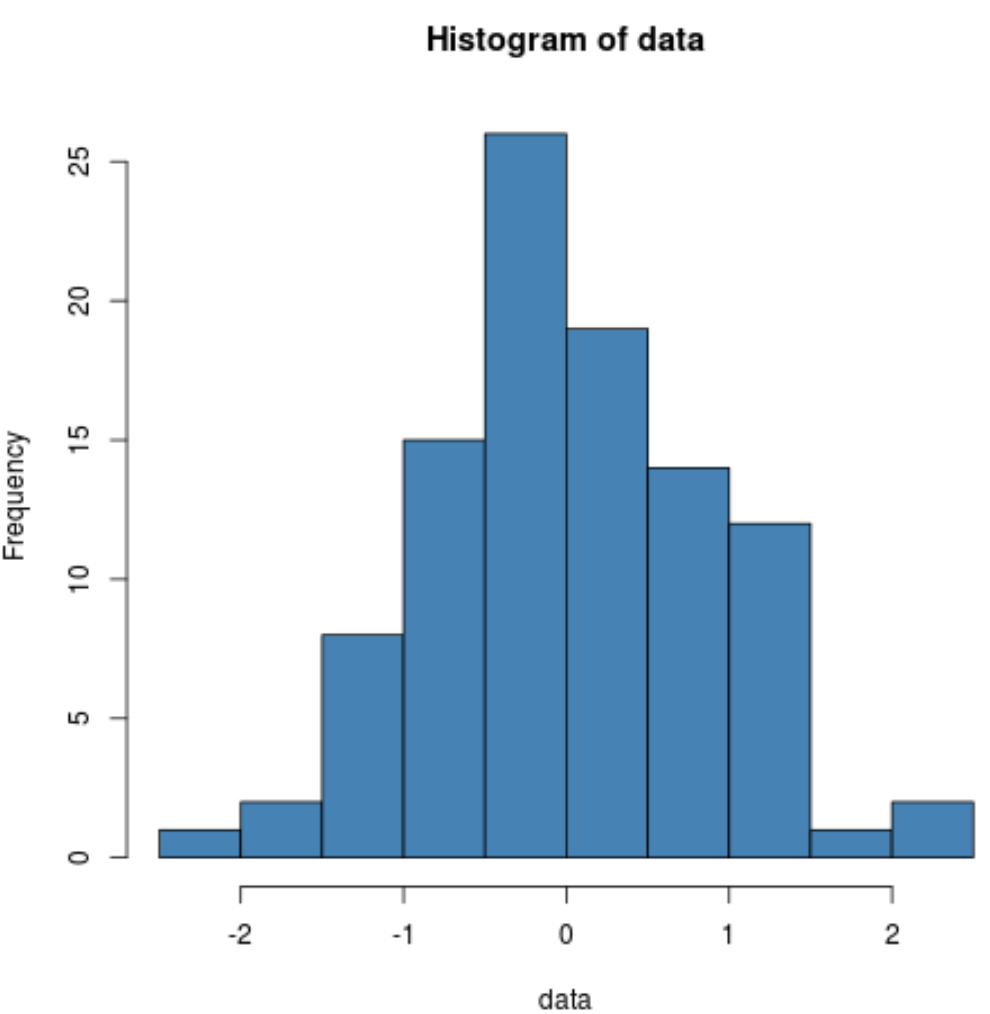
分布は、正規分布データの典型的な、分布の中心にピークを持つ非常に釣鐘型であることがわかります。
例 2: 非正規データに対する Shapiro-Wilk 検定
次のコードは、値がポアソン分布からランダムに生成されるサンプル サイズ n=100 のデータセットに対してシャピロ ウィルク テストを実行する方法を示しています。
#make this example reproducible set.seed(0) #create dataset of 100 random values generated from a Poisson distribution data <- rpois(n=100, lambda=3) #perform Shapiro-Wilk test for normality shapiro.test(data) Shapiro-Wilk normality test data:data W = 0.94397, p-value = 0.0003393
検定の p 値は0.0003393であることがわかります。この値は 0.05 未満であるため、サンプル データが正規分布した母集団からのものではないと言える十分な証拠があります。
ポアソン分布からランダムな値を生成する rpois() 関数を使用してサンプル データを生成したため、この結果は驚くべきことではありません。
関連: R の dpois、ppois、qpois、および rpois のガイド
ヒストグラムを作成して、サンプル データが正規分布していないことを視覚的に確認することもできます。
hist(data, col=' coral2 ')
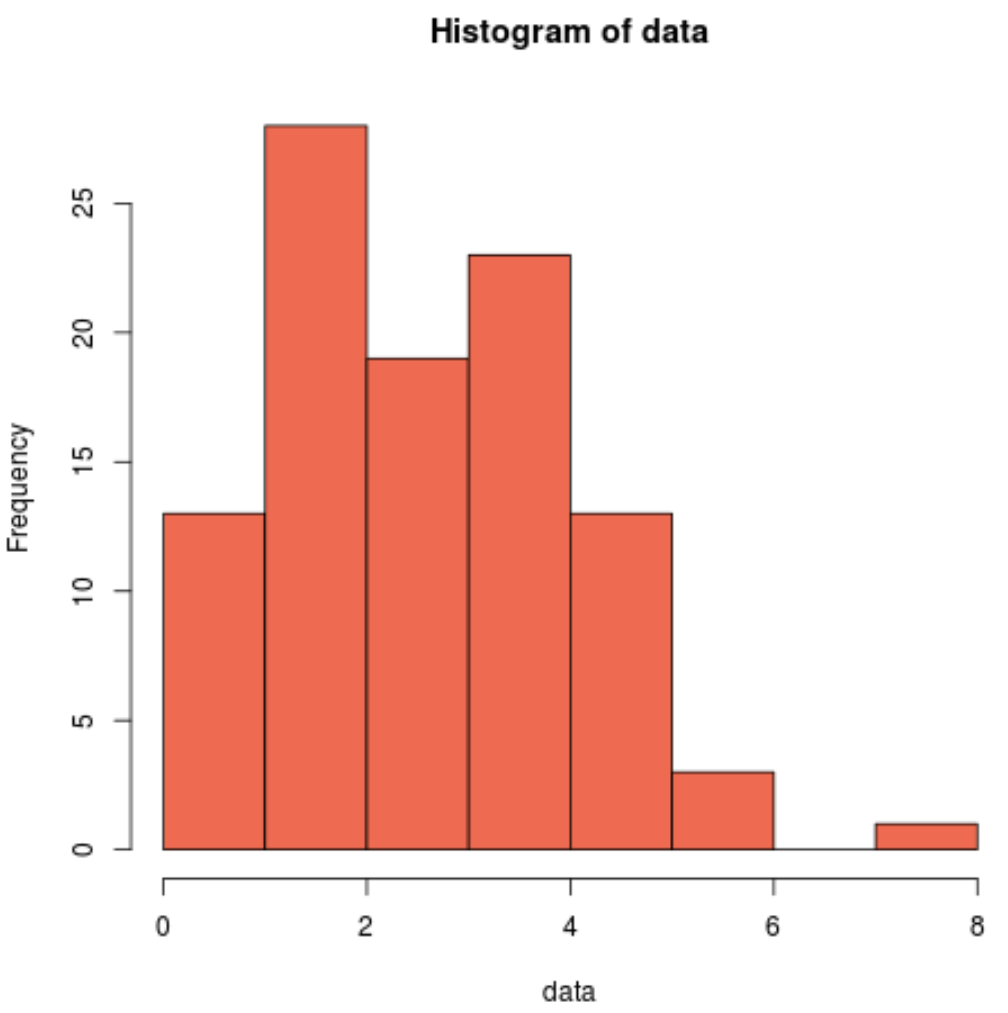
分布は右に歪んでいて、正規分布に伴う典型的な「釣鐘型」ではないことがわかります。したがって、ヒストグラムは Shapiro-Wilk 検定の結果と一致しており、標本データが正規分布からのものではないことが確認されます。
非正規データをどうするか
特定のデータセットが正規分布していない場合は、多くの場合、次のいずれかの変換を実行して、より正規化することができます。
1. 対数変換:応答変数を y からlog(y)に変換します。
2. 平方根変換:応答変数を y から√yに変換します。
3. 立方根変換:応答変数を y からy 1/3に変換します。
これらの変換を実行することにより、応答変数は通常、正規分布に近似します。
これらの変換を実際に実行する方法については、 このチュートリアルを参照してください。
追加リソース
R でアンダーソン・ダーリング検定を実行する方法
R でコルモゴロフ・スミルノフ検定を実行する方法
Python で Shapiro-Wilk テストを実行する方法