スネデコール f ディストリビューション
この記事では、Snedecor F ディストリビューションとは何か、またその用途について説明します。さらに、Snedecor F 分布グラフとその統計的特性を確認することができます。
スネデコール F 分布とは何ですか?
スネデコール F 分布 は、フィッシャー・スネデコール F 分布または単にF 分布とも呼ばれ、統計的推論、特に分散分析で使用される連続確率分布です。
Snedecor F 分布の特性の 1 つは、自由度を示す 2 つの実数パラメーターmとnの値によって定義されることです。したがって、Snedecor 分布 F のシンボルはF m,nです。ここで、 mとnは分布を定義するパラメーターです。

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
➤参照:カイ二乗分布とは何ですか?
フィッシャー・スネデコール F 分布の名前は、イギリスの統計学者ロナルド フィッシャーとアメリカの統計学者ジョージ スネデコールに由来しています。
統計では、Fisher-Snedecor F 分布はさまざまな用途に使用できます。たとえば、Fisher-Snedecor F 分布はさまざまな線形回帰モデルを比較するために使用され、この確率分布は分散分析 (ANOVA) で使用されます。
スネデコール F 分布図
Snedecor F 分布の定義を確認したら、その密度関数のグラフと累積確率のグラフを以下に示します。
以下のグラフでは、さまざまな自由度を持つ Snedecor F 分布の例をいくつか見ることができます。
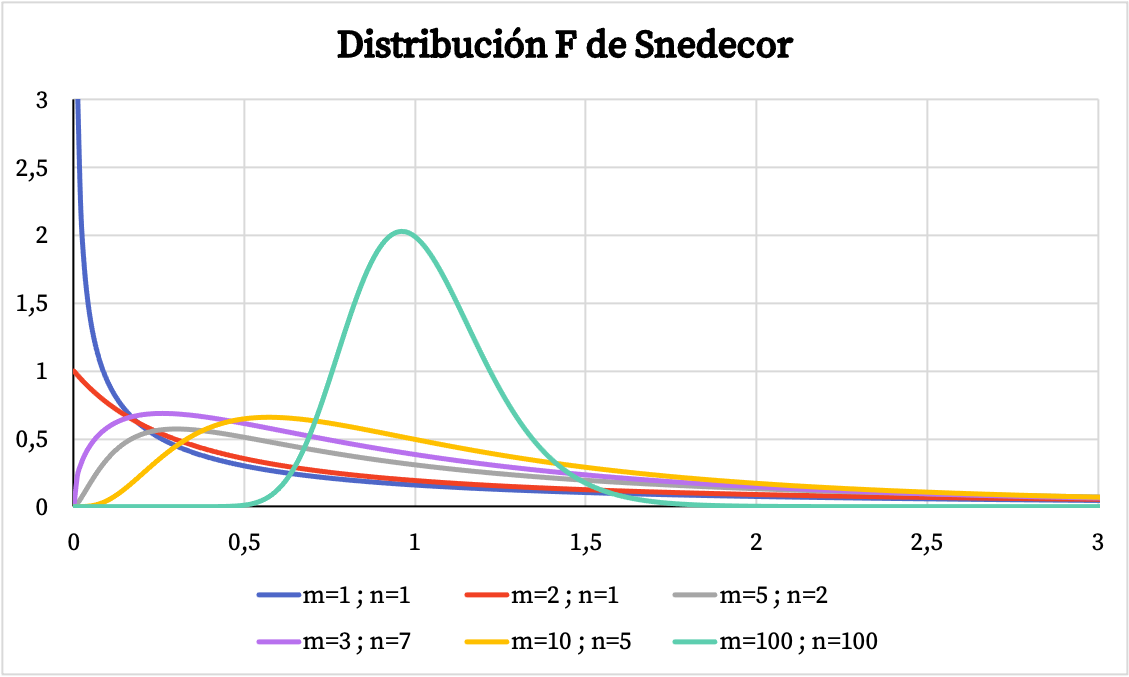
一方、以下のグラフでは、Snedecor F 分布の累積確率関数のグラフが特性値に応じてどのように変化するかがわかります。
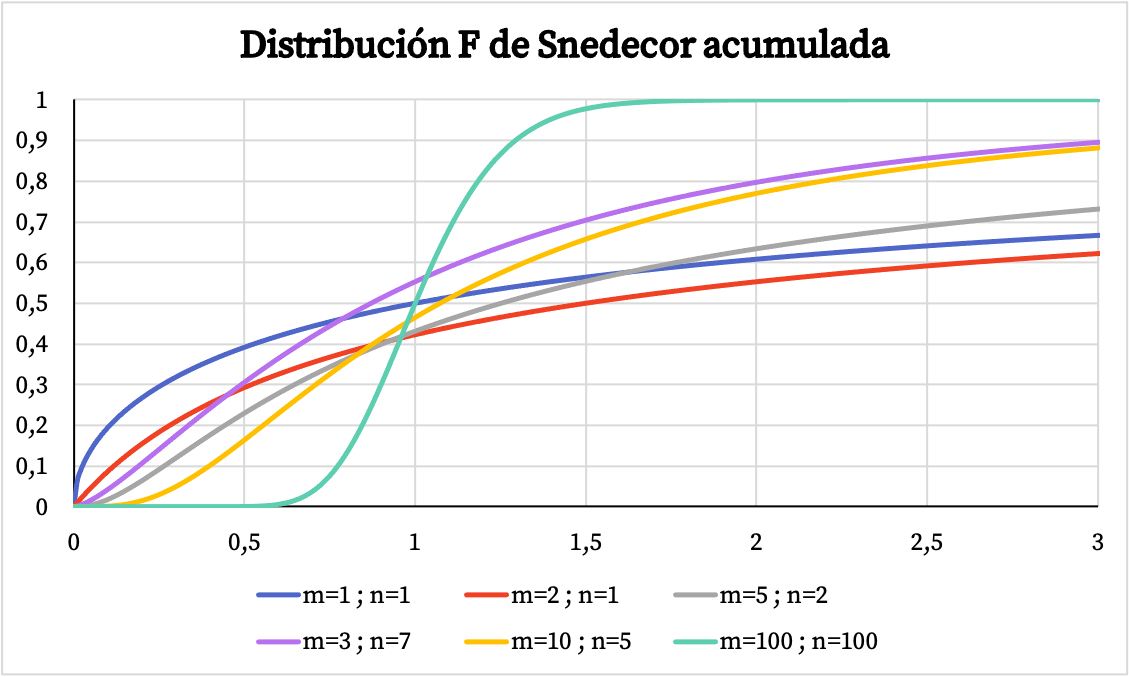
Snedecor F 分布の特徴
最後に、このセクションでは、Snedecor F 分布の最も重要な特性を示します。
- Snedecor F 分布の自由度mとnは、分布の形状を定義する 2 つのパラメーターです。 Snedecor F 分布のこれらの特性値は正の整数です。
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Snedecor F 分布の領域は、ゼロ以上のすべての実数で構成されます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- nの値が 2 より大きい場合、Snedecor F 分布の平均は、 nから 2 を引いた値のnに等しくなります。
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>パラメーター<em>n</em>が 2 より大きい場合、Snedecor 分布 F の分散は、次の式を適用して計算できます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>パラメーター<em>m</em>が 2 より大きい場合、Snedecor 分布 F の最頻値は次の式で計算できます。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
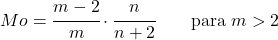
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- 変数が自由度mおよびnの Snedecor F 分布に従う場合、その変数の逆関数は同じ自由度を持つ Snedecor F 分布に従いますが、その値の順序は変わります。
![]()
- Student 分布は、Snedecor F 分布と次の関係があります。
![]()