スピアマンのランク相関を使用する場合 (2 つのシナリオ)

2 つの変数間の線形関連を定量化する最も一般的な方法は、 ピアソン相関係数を使用することです。ピアソン相関係数は常に -1 から 1 までの値を取ります。

• -1 は完全な負の線形相関を示します。
• 0 は線形相関がないことを示します
• 1 は完全な正の線形相関を示します。

ただし、このタイプの相関係数は、2 つの変数間の真の基礎となる関係が線形である場合に最も効果的に機能します。

スピアマン順位相関と呼ばれる別のタイプの相関係数があり、これは 2 つの特定のシナリオで最適に使用されます。

シナリオ 1 : 機密データを扱う場合。

• 例としては、クラス内の生徒の数学試験のスコアのランキングと科学試験のスコアのランキングを含むデータセットが考えられます。

シナリオ 2 : 1 つ以上の極端な外れ値が存在する場合。

• データセットに極端な外れ値が存在する場合、ピアソン相関係数は大きな影響を受けます。

次の例は、これらの各シナリオでスピアマンのランク相関を計算する方法を示しています。

シナリオ 1: スピアマンのランキングとランク付けされたデータの相関関係

2 つの変数間の関係を示す次のデータ セット (および対応する散布図) を考えてみましょう。

統計ソフトウェアを使用すると、これら 2 つの変数について次の相関係数を計算できます。

• ピアソン相関: 0.79
• スピアマンのランク相関: 1

このシナリオでは、データ値のランクのみを気にする場合 (x のランクが増加すると、y のランクも増加しますか?)、スピアマンのランク相関により、より良いアイデアが得られます。 2 つの変数間の相関関係。 。

この特定のデータセットでは、x のランクが増加すると、y のランクも常に増加します。

スピアマンの順位相関は、x の順位と y の順位の間に完全な正の関係 ( ρ = 1 ) があることを示し、この動作を完全に捉えています。

一方、ピアソン相関は、2 つの変数間に強い線形関係 ( r = 0.79 ) があることを示しています。

これは真実ですが、x のランクと y のランクの間の関係だけを気にする場合は役に立ちません。

シナリオ 2: スピアマンのランキングと極端な外れ値の相関関係

2 つの変数間の関係を示す次のデータ セット (および対応する散布図) を考えてみましょう。

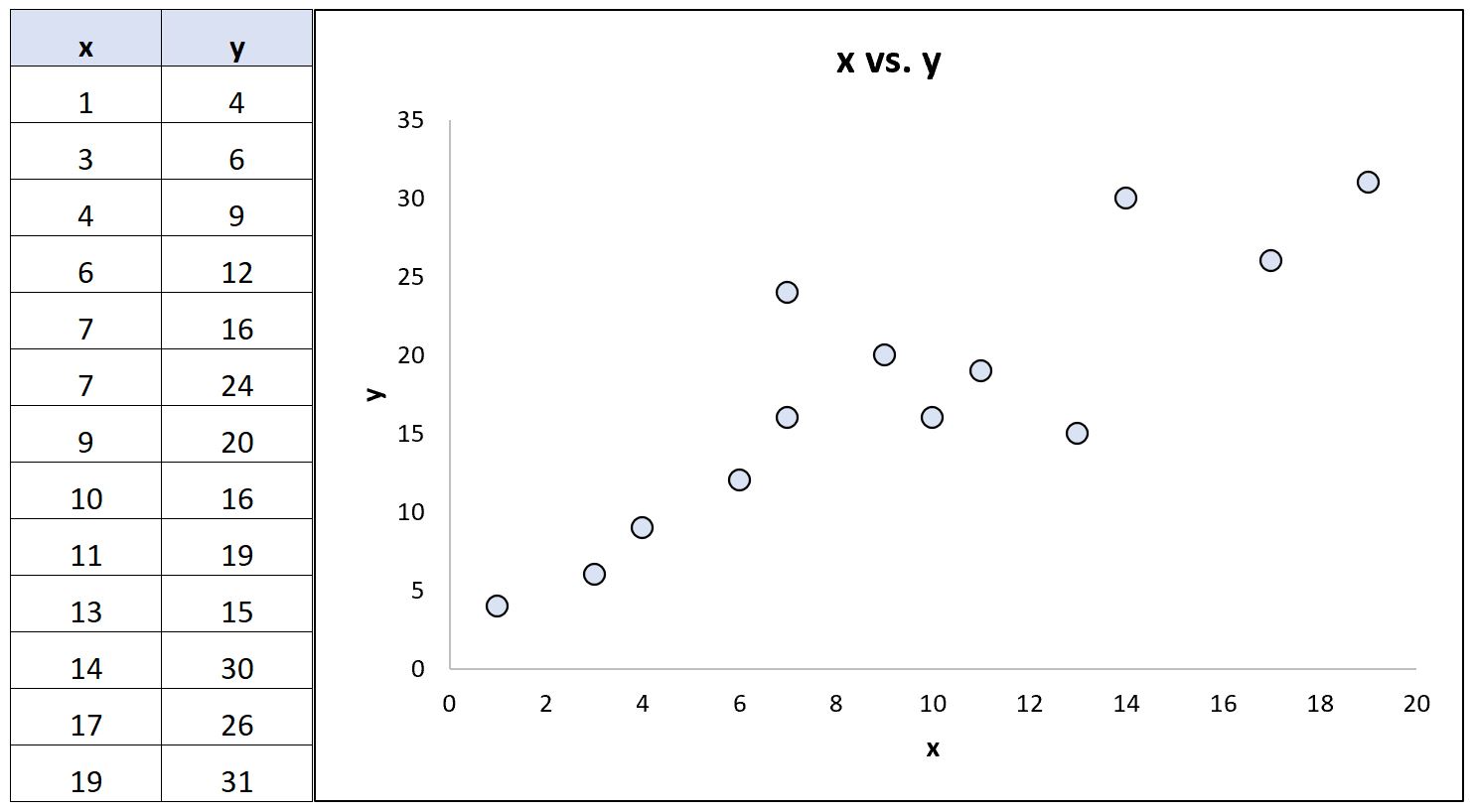
統計ソフトウェアを使用すると、これら 2 つの変数について次の相関係数を計算できます。

• ピアソン相関: 0.86
• スピアマンのランク相関: 0.85

変数間の基礎的な関係がほぼ線形であり、極端な外れ値がないため、相関係数はほぼ同一です。

ここで、データセット内の最後の y 値を変更して、極端な外れ値になるとします。

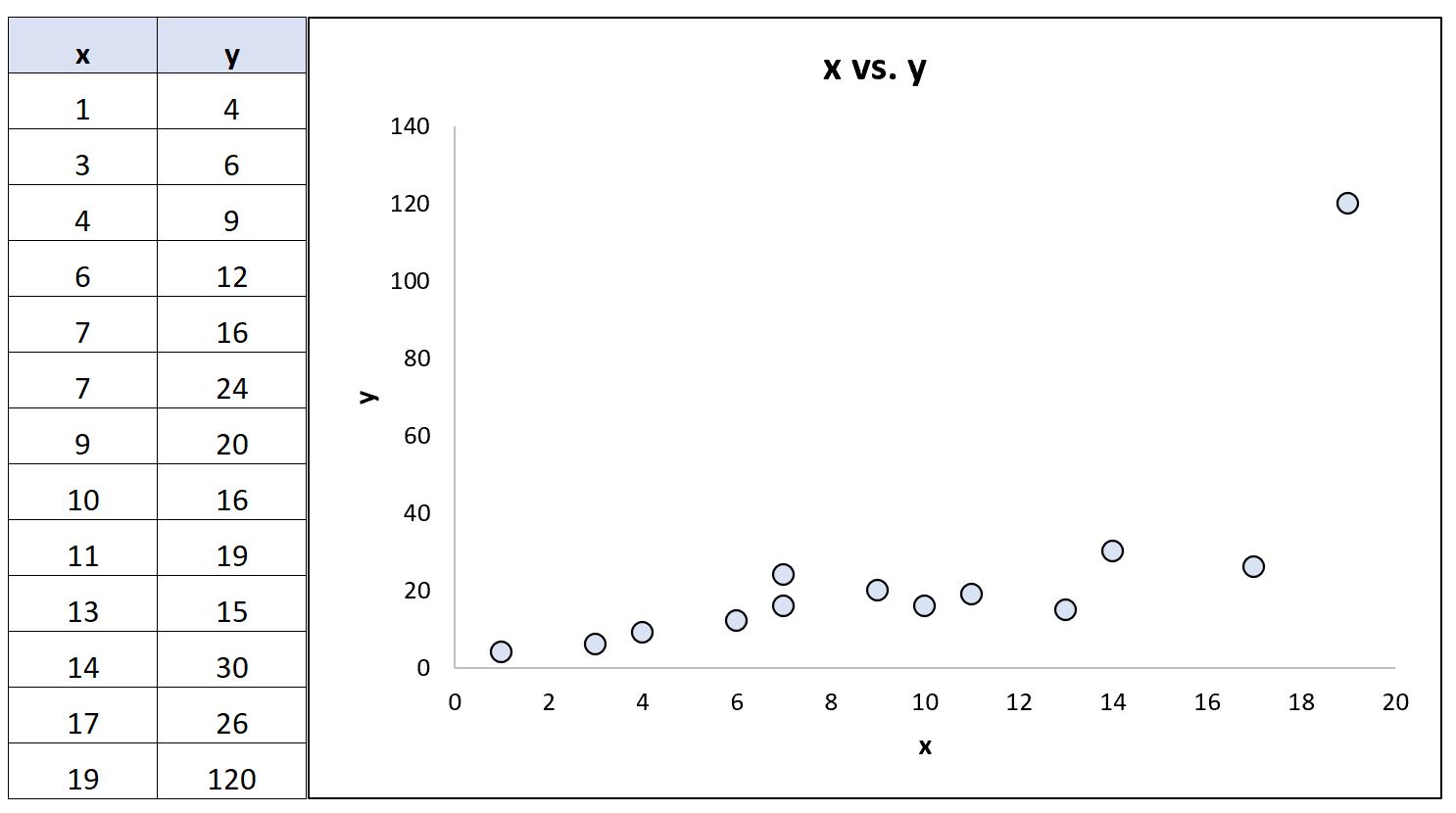
統計ソフトウェアを使用すると、相関係数を再計算できます。

• ピアソン相関: 0.69
• スピアマンのランク相関: 0.85

ピアソン相関係数は大幅に変化しましたが、スピアマン順位相関係数は同じままでした。

統計用語を使用すると、x と y の関係は単調である (x が増加すると、一般に y も増加する) が、外れ値がデータに大きな影響を与えるため、線形ではないと言えます。

このシナリオでは、スピアマンの順位相関はこの単調な関係を適切に定量化しますが、ピアソンの相関は 2 つの変数間の線形関係を計算しようとするため、うまくいきません。

関連: Spearman ランク相関を APA 形式でレポートする方法

追加リソース

次のチュートリアルでは、さまざまなソフトウェアを使用して Spearman 順位相関を計算する方法を説明します。

Excel でスピアマンのランク相関を計算する方法
Google スプレッドシートでスピアマンの順位相関を計算する方法
R でスピアマンの順位相関を計算する方法
Python で Spearman の順位相関を計算する方法