標準偏差ゼロを解釈する方法
統計学では、標準偏差はサンプル内の値の分布を測定するために使用されます。
次の式を使用して、特定のサンプルの標準偏差を計算できます。
√ Σ(x i – x bar ) 2 / (n-1)
金:
- Σ: 「和」を意味する記号
- x i :サンプルのi 番目の値
- x bar :サンプルの平均値
- n:サンプルサイズ
標準偏差値が高いほど、 サンプル内での値の分散が大きくなります。
標準偏差値が低いほど、値はより密接にグループ化されます。
サンプルの標準偏差がゼロの場合、サンプル内のすべての値がまったく同じであることを意味します。
言い換えれば、値の間にギャップはありません。
次の例は、実際に標準偏差 0 を解釈する方法を示しています。
例: 標準偏差ゼロを解釈する方法
10 匹のトカゲの 単純なランダム サンプルを収集し、その体長 (インチ単位) を測定するとします。
長さ: 7、7、7、7、7、7、7、7、7、7
サンプル内のトカゲの平均体長は 7 インチです。
これを知ることで、このデータセットのサンプル標準偏差を計算できます。
- s = √ Σ(x i – x bar ) 2 / (n-1)
- s = √ ((7 – 7) 2 + (7 – 7) 2 + (7 – 7) 2 + … + (7 – 7) 2 / (10-1)
- s = √ 0 2 + 0 2 + 0 2 + … + 0 2 / 9
- s = 0
標本の標準偏差は0であることがわかります。
各トカゲの長さはまったく同じであるため、データセット内の値の分布は正確にゼロになります。
現実の世界でも標準偏差がゼロになることはあるのでしょうか?
実際のデータセットの標準偏差がゼロになることは十分にあり得ますが、それはまれです。
標準偏差 0 が発生する可能性が最も高いシナリオは、まれなイベントの小さなサンプルを収集する場合です。
たとえば、特定の都市で 1 週間の交通事故の数に関するデータを収集するとします。
次のデータを収集する可能性は十分にあります。
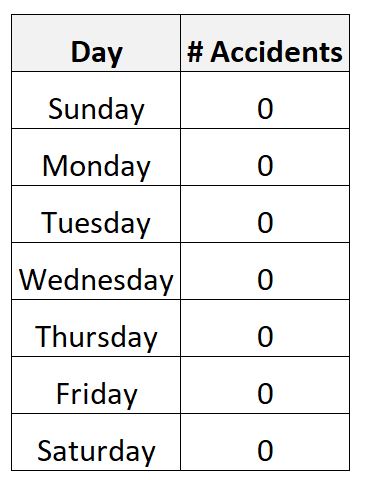
このシナリオでは、1 日あたりの平均事故数はゼロになり、標準偏差もゼロになります。
あるいは、企業の高価な製品の 6 か月間の月次販売数に関する次のデータを収集するとします。
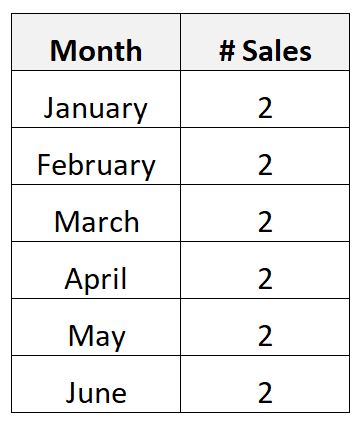
この製品は非常に高価であるため、同社では月にちょうど 2 個しか売れないことが判明しました。
このシナリオでは、月間販売製品の平均数は 2 で、月間販売製品の標準偏差は 0 です。
実際のデータセットで標準偏差がゼロになった場合は、データセット内のすべての値がまったく同じであることを意味することを知っておいてください。
追加リソース
次のチュートリアルでは、統計における標準偏差に関する追加情報を提供します。